ISSN 0798 1015

Vol. 41 (Nº 09) Año 2020. Pág. 15

El rol del docente en la argumentación matemática de estudiantes para la resolución de problemas

Role of the teacher in the mathematical argumentation of students for problem solving

VALBUENA DUARTE, Sonia 1; MUÑIZ MÁRQUEZ, Luz E. 2 y BERRIO VALBUENA, Jesús D. 3

Recibido: 06/11/2019 • Aprobado: 28/02/2020 • Publicado: 19/03/2020

Contenido

1. Introducción

2. Metodología

3. Resultados

4. Conclusiones

Referencias bibliográficas

1. Introducción

La directriz del Ministerio de Educación Nacional (MEN) en Colombia, para la enseñanza de las matemáticas es potenciar en los estudiantes habilidades y destrezas para ser matemáticamente competentes (MEN, 2006), y en documentos como Lineamientos Curriculares en Matemáticas (MEN, 1998), se enfatiza el rol del profesor como orientador del proceso de enseñanza y aprendizaje de los estudiantes, donde el aula se convierte en un medio para construir saberes y donde el estudiante genera aprendizaje a partir de experiencias significativas donde debe intervenir de forma permanente, donde la comunicación es esencial para generar razonamientos y argumentos a la hora de resolver un problema. Siendo así, la argumentación matemática, es considerada parte esencial de la formación de los estudiantes en las distintas etapas escolares, como se evidencia en otros documentos emanados por el MEN, como la Matriz de Referencia basado en los Estándares Básicos de Competencias (EBC), que permite establecer la relación entre las competencias, los componentes acompañados de los aprendizajes y evidencias de aprendizaje (Instituto Colombiano para el Fomento de la Educación Superior- ICFES).

En otro documento del MEN: los Derechos Básicos de Aprendizaje (DBA), plantea una posible ruta de aprendizaje para que los estudiantes alcancen lo planteado en los EBC (MEN, 2015, MEN, 2016). Siendo la argumentación un elemento que viabiliza estos objetivos, puesto que el aprendizaje de las matemáticas depende de la participación del estudiante en este proceso, marcándose incluso diferentes estados de participación en los procesos de argumentación, lo que permite una descripción de las diferentes etapas en el proceso de aprendizaje de las matemáticas desde la perspectiva de una teoría de la interacción del aprendizaje matemático (Krummheuer,2015).

En este sentido se puntualiza como objeto de estudio la resolución de problemas en función de la argumentación matemática en la básica primaria y el rol del profesor en todo este proceso es clave, Carreño y Ortiz (2018) resaltan una relación cercana entre las condiciones que promueven la argumentación en el aula matemática y la gestión que desarrolla el docente en esta. Sin embargo, en algunos estudios realizados (Jiménez y Pineda, 2013; De Gamboa; Planas y Edo,2010), se han identificado dificultades prácticas y de interpretación alrededor de la argumentación matemática, reportándose la necesidad de analizar en profundidad el uso que hacen profesores y estudiantes de estas prácticas.

En ese sentido Aldana (2014) hace referencia al surgimiento del ejercicio argumentativo  consistente con las metas pedagógicas, lo que se puntualiza en crear estrategias para mejorar efectivamente el desarrollo de la competencia matemática en los niños desde que inician la escuela y que va a influir en su desempeño durante toda su vida escolar (Rincón,2015); ya que la práctica docente tiene un peso relevante en el desarrollo del conocimiento matemático del niño pues su influencia es tanto directa como indirecta.

1.1. Aspectos conceptuales

Goizueta y Planas (2013); Solar y Deulofeu (2014), señalan la importancia del análisis de la argumentación en el aula de matemáticas, en lo referente al uso de los registros discursivos especializados, y Boero; Douek y Ferrari (2002) destacan tres actuaciones discursivas principales del profesor de matemáticas en la gestión especializada de la práctica argumentativa del aula: a) mediación semiótica indirecta, cuando se seleccionan y utilizan producciones lingüísticas de los estudiantes; b) mediación semiótica directa, cuando se provee a los estudiantes de expresiones lingüísticas apropiadas para codificar y controlar procesos de pensamiento y producción, y c) mediación cultural, cuando se aportan modelos válidos de actuación matemática, ya sean lingüísticos o de otra índole. En la teoria de Toulmin (Pinochet, J.,2015), se han identificado los elementos que intervienen en un argumento, como se muestra en la Figura 1.

En ese sentido Stein y Albro (2001); Stein y Bernas (1999), Valbuena, Paternina y Cervantes (2019) afirman que los niños desde la edad de tres años están aptos para comprender y generar todos los componentes del discurso argumentativo. Pues, desde esta edad hasta los cinco años tienen conocimiento acerca de la forma, contenido y funciones de los argumentos. Desenvolviéndose mejor en contextos orales, haciendo uso de sus habilidades argumentativas en todo tipo de interacciones y están en la capacidad de dar razones lógicas frente a un debate. Adicionalmente, Larraín y Olivos (2014) y Pedreros (2017), ven fundamental la argumentación en las matemáticas, en la comunicación de resultados en un lenguaje matemático, en dilucidar mecanismos, transmitir y asentar a partir de juicios inductivos.

Figura 1
Esquema del modelo
de Toulmin

Fuente: Tomado de Goizueta  y Planas (2013)

Con base en las categorías establecidas porErduran, Osborne y Simon, (2004), los autores Romero, Bonilla y Álvarez (2018), proponen 6 niveles, que varían en complejidad de procesos evidenciados, numerándose desde el nivel cero (0) hasta el cinco (5). En la Tabla 1, se presentan sus descripciones.

Tabla 1
Niveles de la competencia argumentativa

Fuente: Tomada de Romero, Bonilla y Álvarez (2018)

-----

Es fundamental, tener presente la didáctica como eje principal del proceso de enseñanza y aprendizaje, pues esto resulta en un proceso de índole comunicativo en el aula, cuya competencia docente es clave para aumentar la conciencia y para entender las dificultades a las que se enfrentan los estudiantes para conseguir tomar control de su propio aprendizaje (Coloma; Juca y Celi, 2019); Corbalán et al.,2011). Con la intervención directa del profesor, es deseable generar en el estudiante el deseo de aprender y convertirse en autodidacta, planteándose metas alcanzables, estimulándole a plantear y resolver problema matemáticos aplicables a la realidad propia, pudiendo modificar el conocimiento con respecto al medio y a los estímulos recibidos, más no como obligación para poder aprobar un curso. Y en este sentido la resolución de problemas juega un papel bien importante en el aprendizaje de la matemática, convirtiéndose en el vehículo y la razón de ser para aprenderla.

Schoenfeld (1985), Andrade y Narváez (2016) definen la resolución de problemas como: el uso de proyectos por medio de los cuales los estudiantes aprenden a pensar matemáticamente y Echenique (2006) considera que es una competencia en la que se pone de manifiesto la habilidad de las personas y el grado de desarrollo de destrezas. Es la principal finalidad del área, entendida no solamente como la resolución de situaciones problemáticas propias de la vida cotidiana, sino también de las que no resulten tan familiares. La resolución de problemas precisa de una planificación de las acciones a llevar a cabo, que ayuden a situar y utilizar adecuadamente los conocimientos adquiridos. La resolución de problemas es la actividad más complicada e importante que se plantea en Matemáticas. Los contenidos del área cobran sentido desde el momento en que es necesario aplicarlos para poder resolver una situación problemática.

Y con este panorama, la resolución de problemas y la argumentación juegan un rol vital en el proceso de enseñar y aprender matemática, a partir de autores con grandes aportes en estos dos aspectos, se ha diseñado una articulación entre estas dos categorías, pues tradicionalmente se han estudiado de manera separada, esta articulación es mostrada en la Figura 2.

Figura 2
Esquema sobre las semejanzas entre la resolución de
problemas, las acciones y procesos de la argumentación

Fuente: Elaboración propia

En la enseñanza de las matemáticas es necesario que el profesor analice y realice seguimiento monitoreado de sus prácticas de aula de clases, incorporando habilidades profesionales que le faciliten una gestión de la clase en mejores condiciones para obtener los resultados esperados (Arévalo,2015), valorando como pieza clave el contexto escolar, ya que es el verdadero agente del desarrollo del currículo (SEP, 2009), y analizar las variables didácticas como el trabajo en equipo, la colaboración entre maestros; estas acciones estimulan al profesor a seguir transformando su práctica, que dé prioridad a los procesos (Hernández; Prada; Ramirez, y Fernández,2018), al razonamiento, a la resolución de problemas, a la interpretación y explicación de resultados, dejando de lado el abuso en el empleo de algoritmos o la mera memorización y utilización de reglas (Villella, 2004), lo que sin duda le estimula a modificar sus creencias sobre lo que representa enseñar matemática; que en muchos casos es pensada como proporcionar definiciones y resolver expresiones alejadas de ser situaciones de aprendizajes.

Ivars; Fernández y Llinares (2018) y Llinares; Ivars; Buforn y Groenwald, (2019) establecen el uso del conocimiento de matemáticas y de la didáctica de las matemáticas para reconocer elementos relevantes en las situaciones de enseñanza de las matemáticas, interpretarlas y apoyar las decisiones de acción. Esta competencia ayuda a los estudiantes y al docente a describir, explicar y anticipar aspectos que pueden condicionar el desarrollo de la enseñanza, por medio de la trayectoria hipotética de aprendizaje como mecanismo de ayuda a los estudiantes para que el docente genere un discurso con detalles sobre el pensamiento matemático de los estudiantes y a proponer actividades centradas en la comprensión relacionando la capacidad para atender a los detalles y la habilidad para proponer actividades para apoyar el desarrollo conceptual de los estudiantes. Por lo que, entonces es labor clave del profesor, diseñar y facilitar tareas didácticas en las que sus estudiantes actúen empleando su potencial conforme a los aprendizajes esperados en los diferentes procesos; para nuestro interés: la argumentación, con el firme propósito de que lleguen a ser matemáticamente competentes. Que se vea no como la única persona que sabe lo que hay que hacer en la clase (Lee, 2006; Pochulu; Font, y Rodríguez, 2016), su función de mediación supone ocuparse de la enseñanza y ayudar a sus estudiantes en su proceso de aprendizaje para que progresivamente se hagan cargo del mismo.

De acuerdo con Bodur (2003), Handal (2003), Moreno, (2000) y Azcárate y Moreno (2006), las creencias del profesor son ideas poco elaboradas, asociadas a las ideas personales, forman parte del conocimiento que este posee, pero carecen de rigor para mantenerlas e influyen de manera directa en su desempeño. Estas  consisten en la estructura que cada profesor de matemáticas da a sus conocimientos para posteriormente enseñarlos o transmitirlos a sus estudiantes (D’Amore y Fandiño, 2004; Ruiz, 1994; Azcarate, García y Moreno, 2006; Bohórquez, 2016). Lo relevante es que sirven como filtro para todo aquello que supone el proceso de enseñanza y aprendizaje.

Ahora bien, López; Aldana y Erazo (2019), consideran que entre las creencias, la formación académica y la trayectoria de cada profesor existe una relación de inclusión que conforma su moldura organizacional de los conceptos. Al respecto Llinares (1991) afirma que las creencias son el contexto psicológico donde se conforman las estructuras personales del conocimiento, de allí emergen las concepciones sobre el desarrollo de los contenidos, así como las trayectorias idóneas para resolver situaciones matemáticas. Para ello, se utilizan ideas producto de la experiencia que toman vida en el aula de clase.

Finalmente, respecto al conocimiento profesional del profesor o, más precisamente, conocimiento del contenido pedagógico, como lo denominan An; Kulm y Wu (2004), es un conocimiento que incluye tres componentes (NCTM, 2000): conocimiento del contenido matemático, conocimiento del currículo (incluye la adecuada selección y uso de materiales curriculares) y conocimiento de la enseñanza (se articula al conocimiento del pensamiento del estudiante, la planificación docente y la destreza en las distintas maneras de enseñar).

El enfoque de investigación empleado es cualitativo, busca las nociones e ideas compartidas que dan sentido al comportamiento social presentado en el objeto de estudio (Bonilla  y Rodríguez 2005) en relación a la argumentación matemática y las prácticas del profesor, para aplicar la resolución de problemas con estudiantes de tercer grado. El objetivo es profundizar en este fenómeno de la argumentación matemática articulado con el quehacer docente, para hacer una aproximación global de esta situación problema, explorarlo, describirlo y comprenderlo de manera inductiva. Es decir, a partir de los conocimientos que tienen las dos profesoras involucradas y sus estudiantes a cargo.

La investigación se fundamenta en el estudio de caso (Jiménez y Comet, 2016), conceptualizando la intención de dar respuesta sobre las prácticas del docente de matemáticas para desarrollar la argumentación matemática a través de la resolución de problemas, focalizando las interpretaciones de los docentes en concordancia con la praxis realizada en el aula de clases (Bonilla  y Rodríguez 2005), las diferentes estrategias usadas y las opciones para superar obstaculos y poder desarrollar esta competencia en los estudiantes, explorando sus creencias o conocimiento sobre la argumentación y en lo que se observa en su quehacer diario como profesor de matemática. Este proyecto se ejecuta en 4 etapas, adaptadas de Montero y León (2002), Jiménez (2012) y Arzola (2019), como descritas a seguir:

1. Selección del caso objeto de estudio: la argumentación matemática y las prácticas del profesor para la resolución de porblemas con estudiantes de tercer grado, buscando indagar sobre la forma como se desarrollan las clases de matemáticas en torno a la argumentación en los estudiantes, competencia que permite la consolidación en el pensamiento matemático.

2. Diseño de instrumentos para recabar información: cuestionario socio-demográfico y de preguntas abiertas para conocer las interpretaciones del profesor en relación a la argumentación matemática y las diversas estrategias utilizadas, seguida de una entrevista y la observación de sus clases. También se aplica una prueba diagnóstica a estudiantes de dos grados para conocer el nivel de argumentación matemática, posteriormente un grupo focal para confrontar posiciones y comentarios en relación a la prueba y a las prácticas desarrolladas por el docente.

3. Análisis de información: a partir de la prueba diagnóstica se identifica el nivel de argumentación de los estudiantes y de las entrevistas con las profesoras, se hace intervención al docente orientada a partir de un conjunto de actividades con el objeto de impactar la competencia argumentación matemática a través de la resolución de problemas.

4. Sistematización: redacción del informe, triangulando la información recolectada para provocar las reflexiones del caso presentado.

2.1.Técnicas e instrumentos para la recolección de información

Cuestionario de preguntas abiertas a docentes

Con 20 preguntas en total, se buscó conocer la concepción de las profesoras sobre la argumentación matemática y las estrategias aplicadas en el aula para potenciarla en los estudiantes, estos cuestionamientos fueron realizados usando las técnicas de entrevista y grupo focal.

Cuestionario de conocimientos aplicados a los estudiantes de los dos grupos objeto de estudio: tercero A y tercero C

Se diseñan dos pruebas que permiten visualizar la comprensión del estudiante en la resolución de problemas. Las dos pruebas son aplicadas en formato impreso a los dos grupos de estudiantes (Figura 3). La primera prueba con cinco preguntas y la segunda con seis; en los dos casos las preguntas son tomadas de las pruebas SABER 3° (ICFES 2015-2016), las cuales son validadas bajo el método de respuesta al ítem.

En el diseño de la primera prueba (identificada como Prueba diagnóstica), las preguntas 1, 2 y 4 buscan conocer a través de la justificación, los procedimientos realizados por el estudiante al resolver una situación problema; mientras que las preguntas 3 y 5 solo permiten conocer la respuesta escogida.

Para la segunda prueba (Prueba final), enlas preguntas 1, 2, 4, 5 y 6 se pide justificación de los procedimientos realizados; mientras enla pregunta 3 solo se conoce la comprensión del estudiante y su asertividad al escoger la respuesta correcta.

Figura 3: Aplicación de prueba diagnóstica y prueba final en el grado tercero A y tercero C.

Los resultados obtenidos por los estudiantes de tercero A y tercero C en la prueba diagnóstica (ver Diagrama 1) los ubica en los primeros dos niveles de argumentación, con la mayor cantidad en los dos grupos, en el nivel más bajo de todas las categorías posibles (ver la Tabla 1).

Diagrama 1
Categorización por niveles de argumentación de los estudiantes de los dos grupos
de estudio frente a una situación problema presentada en la prueba diagnóstica

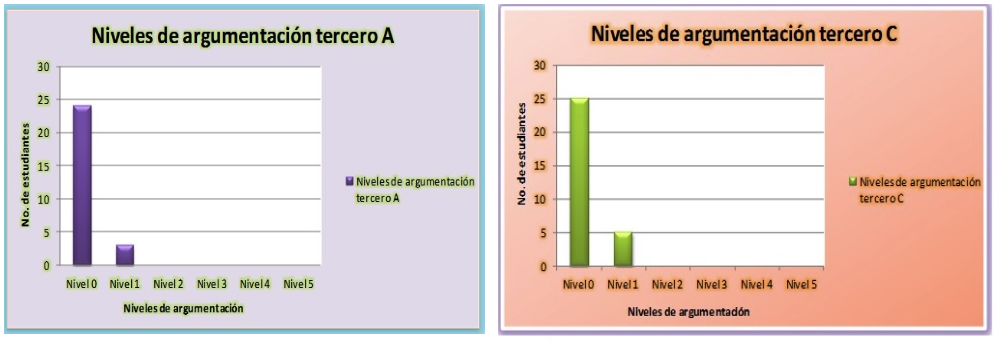
De la información, recabada con los instrumentos aplicados a las profesoras, se encuentra ausencia de un proceso claro que dé cuenta de cómo desarrolla en sus clases procesos que conlleven a la resolución de problemas y a potenciar la argumentación como elemento importante en el aprendizaje de la matemática. En la Figura 4, se presentan las respuestas de las profesoras a la pregunta en torno a lo que puede entenderse como la creencia de qué es para ellas argumentar.

Figura 4
Aplicación de cuestionario
oral a docentes

Con base en el análisis de esta información desde los procesos desarrollados por las profesoras en sus clases y los desempeños de los estudiantes en las pruebas aplicadas, se logró una fotografía de los procesos de argumentación matemática; y a partir de ello se diseñan secuencias didácticas con cinco actividades, presentadas a las dos profesoras de tercero A y tercero C, validándose la apropiación y desarrollo de la argumentación matemática en el aula de clases para la resolución de problemas. Los datos se analizaron con base a los referentes teóricos de la investigación. Posteriormente se dialogó con las docentes para conocer apreciaciones en cuanto a las pruebas y a las actividades realizadas.

3.1. Interpretación de las actividades orientadas a la profesora de matemáticas

 Después de realizadas las actividades el rol de la profesora de tercero C (Figura 5), es analizado a la luz de referentes como Rojas y Valdivieso (2017), Jiménez y Díaz (2003), Weston (2006), Soto (2018) y Echenique (2006), encontrándose una actitud frente a las situaciones planteadas para que ella las desarrollara en su clase, centrada en generar razones a favor o en contra de una afirmación o línea de acción a partir del debate del problema planteado. Así mismo la profesora buscaba desarrollar planificación de las acciones llevadas a cabo, que ayudaran a situar y utilizar adecuadamente los conocimientos adquiridos, en cuanto a las operaciones básicas de la matemática.

En relación a las actuaciones discursivas de las prácticas de la argumentación en el aula de clases, la profesora involucró en su práctica la mediación semiótica directa, indirecta y la mediación semiótica cultural, entendidas a la luz de Boero, Douek y Ferrari (2002) y Goizueta y Planas (2013), para generar en los estudiantes avance y progreso en los niveles argumentativos acompañado de estrategias didácticas que despertaran el interés y motivación. En ese sentido, la práctica de aula de la profesora, entendida bajo la teoría de Guerra, Leguízamo y Rincón, (2016), es producto de la apropiación de las temáticas y de la gestión acertada en el salón de clases incorporando (Arévalo, 2015) habilidades profesionales que le facilitaron condiciones para obtener los resultados esperados producto de generar tareas matemáticas (Goñi,2011) que contribuían a que se desarrollara la actividad matemática en los estudiantes, para ser vistas como instrumentos para el aprendizaje y desarrollo de la argumentación matemática.

En términos de apreciaciones después de realizar la retroalimentación con la profesora de tercero C, comenta: “la importancia de conocer por medio de las pruebas los niveles de los estudiantes en argumentación, me sentí bien, ya que las actividades me ayudaron a conocer las formas como trabajar la argumentación a partir de situaciones problemas en el aula de clases, sin embargo observé que dado que no hemos trabajado de esa manera las clases aún no tengo la práctica completa y a los estudiantes se les ha dificultado también”.

Figura 5
Aplicación de actividades
en tercero C

Los resultados de la prueba final (Diagrama 2) de los estudiantes de tercero C, muestran un progreso relativo encontrándose 15 estudiantes en el nivel 1 y 7 en el nivel 2 de argumentación y ninguno en el nivel cero, lo que marca claros progresos comparados con la prueba diagnóstica, animando a la profesora y a los estudiantes y sobre todo se inicia un camino por recorrer, puesto que la argumentación es un proceso y no un resultado eventual.

En el caso del grado tercero A, se presentan a la profesora las secuencias didácticas y se dialogan las orientaciones para su desarrollo, más ella asumió en las primeras actividades desarrollar sus clases en forma habitual, y pese a que en las entrevistas decía ponderaba la argumentación en los estudiantes, no se evidenció en su praxis, siendo claro que las intervenciones del docente son clave para mejoría del estudiante (Conner; Singletary; Smith; Wagner y Francisco,2014, Solar, Deulofeu, 2016; Solar,2018; Buitrago; Mejía y Hernández, 2013). En este caso no se generaron prácticas argumentativas en profesora ni en estudiantes, solo se logró que aplicara la penúltima actividad (Figura 6), no siendo suficiente para impactar en estudiantes su nivel de argumentación, no superando el obtenido en la prueba diagnóstica (ver Diagrama 4). Aún cuando no hay un momento único para la argumentación (Krummheuer, 1995), y en experiencias de aula cualquier actividad con intencionalidad puede generar procesos argumentativos, siendo necesario despertar el interés en el estudiante para que exprese sus razonamientos y la comprensión de las temáticas, incentivando el diálogo y la autoregulación de las estrategias utilizadas para resolver una situación problema.

La profesora de tercero A, comenta: “las actividades están bien diseñadas, encaminadas a mejorar en estudiantes el razonamiento y la resolución de problemas, y en cuanto a la argumentación eso es un proceso que se está desarrollando lentamente y necesita apoyo de la escuela, de los padres y de los estudiantes”.

Figura 6
Aplicación de actividades
en tercero A

-----

Diagrama 2
Categorización por niveles de argumentación prueba final grado tercero A

Es importante que en el aula de clase se genere un ambiente reflexivo por parte del estudiante y también del docente, por lo que se hace necesario, una buena preparación previa estableciendo tareas que permitan construir el conocimiento formal desde el aporte individual de los estudiantes; este proceso contribuirá en ambientes eficientes a la hora de proporcionar el saber, debido a que el interés del estudiante se va a estimular con anticipación y con su participación espontánea en las clases.

Así pues, Hernández (2009) indica que la argumentación en el área matemática influye en el desarrollo del pensamiento del individuo, así como en la adquisición de nuevos conocimientos, los cuales van siendo construidos por el estudiante partiendo de su entorno tal como lo evidencia es sus estudios Pachón, Parada y Chaparro (2016), ya que esta debe estar acompañada del análisis de la participación. El aprendizaje de las matemáticas depende de la participación del estudiante en los procesos de argumentación, lo que permite una descripción de las diferentes etapas en el proceso de aprendizaje de las matemáticas desde la perspectiva de una teoría de la interacción del aprendizaje matemático (Krummheuer, 2015).

Como parte de las reflexiones se propone a los docentes realizar actuaciones discursivas que promuevan la argumentación en los estudiantes (Boero Douek y Ferrari, 2002). Por lo que se considera que la gestión en el aula se centre en actividades que desarrollen en los estudiantes argumentos asertivos que permitan desarrollar los niveles argumentativos. En cuanto a las entrevistas realizadas a las docentes se infiere que ellas no planeaban sus clases en torno a desarrollar la argumentación matemática, a pesar de poseer una concepción sobre dicha competencia.

El generar procesos de reflexión constante de la práctica de los docentes (Parada y Pluvinage, 2014), permite valorar la planeación a través de una organización de contenidos para conducir progresivamente a la consecución de los objetivos de aprendizaje por parte de sus estudiantes.

Aldana Bermúdez, E. (2014). La argumentación como estrategia de enseñanza y de aprendizaje de las matemáticas. Revista cientifíca-Sección educación científica (20), 37-45.

An, S., Kulm, G., & Wu, Z. (2004). The pedagogical content knowledge of middle school, mathematics teachers in China and the US. Journal of Mathematics Teacher Education , 7 (2), 145-172.

Andrade Payares, E. A., & Narváez Cruz, L. M. (2016). Estrategias de comprensión lectora y su influencia en el desarrollo de la competencia de resolución de problemas matemáticos. 3er simposio internacional y 4to coloquio regional de investigaión educativa y pedagógica (págs. 1-15). Monteria: Maestría en Educación SUE Caribe.

Arévalo Vázquez, E. (2015). ¿Cómo se enseñan las matemáticas en la escuela primaria? XIV CIAEM-IACME (págs. 1-12). Chiapas, México: XIV CIAEM-IACME.

Arzola Franco, D. M. (2019). Procesos formativos en la investigación educativa.Diálogos, reflexiones, convergencias y divergencias. Chihuahua, México: Red de Investigadores Educativos Chihuahua AC.

Azcarate, C., García, L., & Moreno, M. (2006). Creencias, concepciones y conocimiento profesional de profesores que enseñan cálculo diferencial a estudiantes de ciencias económicas. Relime , 9 (1), 85-116.

Bodur, Y. (2003). Preservice teachers’ learning of multiculturalism in a teacher. Florida State University. Florida: FSU Digital Library.

Boero, P., Douek, N., & Ferrari, P. L. (2002). Developing mastery of natural language: Approaches to theoretical aspects of mathematics. Londres, Reino Unido: LEA: En L. D. English (ed.). International Handbook of Research in Mathematics Education.

Bohórquez Arenas, L. Á. (2016). Cambios de concepciones de estudiantes para profesor sobre su gestión del proceso de enseñanza-aprendizaje en ambientes de aprendizaje fundamentados en la resolución de problemas. Universidad Distrital Francisco José de Caldas, Cundinamarca. Bogotá D.C.: Facultad de ciencias y educación.

Bonilla Castro, E., & Rodríguez Sehlk, P. (2005). Más allá del dilema de los métodos (Tercera edición ed.). Bogotá, Colombia: Norma.

Buitrago Martín, Á. R., Mejía Cuenca, N. M., & Hernández Barbosa, R. (2013). La argumentación: de la retórica a la enseñanza de las ciencias. Innovación Educativa , 13 (63), 17-40.

Carreño Díaz, C., & Ortiz Jiménez, A. (2018). Condiciones que promueven la habilidad de argumentar en el aula matemática de una escuela municipal en Chile. Unión revista iberoamericana de educación matemática (54), 60-77.

Coloma Andrade, M. d., Juca Aulestia, J. M., & Celi Carrión, F. N. (2019). Aplicación de las estrategias metodológicas didácticas en matemáticas. Espacios , 40 (17), 29-38.

Conner, A. M., Singletary, L. M., Smith, R. C., Wagner, P. A., & Francisco, R. T. (2014). Teacher support for collective argumentation: a framework for examining how teachers support students’ engagement in mathematical activities. Educational Studies in Mathematics , 86 (3), p. 401-429 DOI 10.1007/s10649-014-9532-8.

Corbalán, F., Giménez, J., López-Goñi, I., Llinares, S., Penalva, M. C., Planas, N.,... & Vanegas, Y. M. (2011). Didáctica de las matemáticas (Vol. 2). Ministerio de Educación.

D’Amore, B., & Fandiño Pinilla, M. I. (2004). Cambios de convicciones en futuros profesores de matemática de la escuela secundaria superior. Épsilon , 25-43.

De Gamboa, G., Planas, N., & Edo, M. (2010). Argumentación matemática: práticas escritas e interpretaciones. Suma (64), 35-44.

Echenique Urdiain, I. (2006). Matemáticas resolución de problemas (primera ed.). Navarra, España: Gobierno de Navarra. Departamento de Educación.

Erduran, S., Simon, S., & Osborne, J. (2004). Tapping into argumentation: developments in the application of Toulmin’s argument pattern for studying science discourse. Science education , 88 (6), 915-933 DOI 10.1002/sce.20012.

Goizueta, M., & Planas, N. (2013). Temas emergentes del análisis de interpretaciones del profesorado sobre argumentación en clase de matemáticas. Enseñanza de las ciencias , 1 (31), 61-78.

Goñi, J. M. (2011). Didáctica de las Matemáticas. Barcelona: GRAO.

Guerra Ibagué, L. M., Leguízamo Morales, C. P., & Rincón Prada, D. (2016). La práctica docente en la enseñanza de las matemáticas: investigación narrativa a nueve docentes de tres instituciones educativas de Bogotá. Universidad de la Salle, Cundinamarca. Bogotá: Facultad de ciencias de la educación.

Handal, B. (2003). Teachers’ Mathematical Beliefs: A Review. The Mathematics Educator , 13 (2), 47–57.

Hernández, S. (2009). Estrategias didácticas que favorecen el razonamiento lógico-matemático a través de la etnomatemática de los alumnos de tercer ciclo (5° y 6°) de la escuela primaria bilingüe "Vicente Guerrero". Universidad Tangamanga Plantel Huasteca. México: Universidad Tangamanga .

Hernández Suaréz, C. A., Prada Núñez, R., Ramirez Leal, P., & Fernández Cézar, R. (2018). Dominio afectivo y prácticas pedagógicas de docentes de matemáticas: un estudio de revisión. Espacios , 39 (23), 25-34.

Herrera Sepúlveda, D. F. (2012). Evaluación de la competencia argumentativa en matemáticas. Universidad Nacional de Colombia, Antioquia. Medellín: Universidad Nacional de Colombia.

Ivars, P., Fernández, C., & Llinares, S. (2018). Carácterísticas del desarrollo de la competencia mirar profesionalmente el pensamiento de los estudiantes sobre fracciones. En ,. L. Rodríguez-Muñiz, L. Muñiz-Rodríguez, A. Aguilar-González, P. Alonso, F. J. García García, & A. Bruno (Ed.), Investigación en Educación Matemática XXII (págs. 270-279). Gijón: SEIEM.

Jiménez Aleixandre, M. P., & Díaz de Bustamante, J. (2003). Discurso de aula y argumentación en la clase de ciencias: cuestiones teóricas y metodológicas. Enseñanza de las ciencias , 21 (3), 359–370.

Jiménez Chaves, V. E. (2012). El estudio de caso y su implementación en la investigación. Revista Internacional Investigación Ciencias Sociales , 8 (1), 141-150.

Jiménez Chaves, V. E., & Comet Weiler, C. (2016). Los estudios de casos como enfoque metodológico. ACADEMO Revista de Investigación en Ciencias Sociales y Humanidades , III (2), 1-11.

Jiménez Espinosa, A., & Pineda Bohórquez, L. M. (2013). Comunicación y Argumentación en la Clase de Matemáticas. Educación y ciencia (16), 101 - 116.

Krummheuer, G. (2015). Methods for Reconstructing Processes of Argumentation and Participation in Primary Mathematics Classroom Interaction. En A. Bikner, C. Knipping, & P. N., Approaches to Reconstructing Argumentation (págs. 51-74). Springer Science+Business Media Dordrecht.

Krummheuer, G. (1995). The ethnography of argumentation. En P. COBB, & H. BAUERSFELD, The emergence of mathematical meaning: interaction in classroom cultures (págs. 229-269). Hillsdale: Lawrence Erlbaum.

Larraín, A., Freire, P., & Olivos, T. (2014). Habilidades de argumentación escrita: una propuesta de medición para estudiantes de quinto básico. Psicoperspectivas individuo y sociedad , 13 (1), 94-104.

Lee, C. (2006). El lenguaje en el aprendizaje de las matemáticas. Madrid: Morata.

López Leyton, C., Aldana, E., & Erazo, J. D. (2019). El papel de la resolución de problemas para la enseñanza del cálculo integral: un estudio de caso. Espacios , 40 (17), 12-19.

Llinares, S. (1991). La Formación de profesores de matemáticas. Sevilla: GID.

Llinares, S., Ivars, P., Buforn, A., & Groenwald, C. (2019). Mirar profesionalmente las situaciones de enseñanza: una competencia basada en el conocimiento. En E. Badillo, N. Climent, C. Fernández, & M. T. González (Ed.), Investigación sobre el profesor de matemáticas: formación, práctica de aula, conocimiento y competencia profesional (págs. 177-192). Salamanca: Universidad Salamanca.

MEN. (2015). Caja de materiales siempre día E Recuperado de: http://aprende.colombiaaprende.edu.co/es/siemprediae/86437. Bogotá: Ministerio De Educación Nacional.

MEN. (2016). Caja de materiales siempre día E Recuperado de: http://aprende.colombiaaprende.edu.co/es/siemprediae/93216. Bogotá: Ministerio De Educación Nacional.

MEN. (2006). Estándares Básicos de Competencias en Matemáticas. Bogotá: Ministerio De Educación Nacional.

MEN. (1998). Lineamientos curriculares en matemáticas. Bogotá: Magisterio.

Montero, I., & León, O. G. (2002). Clasificación y descripción de las metodologías de investigación en psicología. Revista Internacional de Psicología Clínica y de la Salud , 2 (3), 503-508.

Moreno, M. (2000). El profesor universitario de matemáticas: estudio de las concepciones y creencias acerca de la enseñanza de las ecuaciones diferenciales.Estudio de casos. Universidad Autónoma de Barcelona. Barcelona: Universidad Autónoma de Barcelona.

NCTM. (2000). Principles and standards for school mathematics. Reston: Reston: NCTM.

Pachón Alonso, L. A., Parada Sánchez, R. A., & Chaparro Cardozo, A. Z. (2016). El razonamiento como eje transversal en la construccion del pensamiento lógico. Praxis & Saber , 7 (14), 219 - 243.

Parada, S. E., & Pluvinage, F. (2014). Reflexiones de profesores de matemáticas sobre aspectos relacionados con su pensamiento didáctico. Revista Latinoamericana de Investigación en Matemática Educativa , 17 (1), 83-113 DOI: 10.12802/relime.13.1714.

Pedreros Matta, A. (2017). Desarrollo de habilidades: aprender a pensar matemáticamente. Santiago de Chile: Ministerio de educación de Chile.

Pinochet, J. (2015). El modelo argumentativo de Toulmin y la educación en ciencias: una revisión argumentada. Ciência & Educação (Bauru) , 21 (2), 307-327 DOI: http://dx.doi.org/10.1590/1516-731320150020004.

Pochulu, M., Font, V., & Rodríguez, M. (2016). Desarrollo de la competencia en análisis didáctico de formadores de futuros profesores de matemática a través del diseño de tareas. Revista Latinoamericana de Investigación en Matemática Educativa , 19 (1), 71-98 DOI:https://dx.doi.org/10.12802/relime.13.1913.

Pólya, G. (1965). Cómo plantear y resolver problemas. México D.F.: Trillas.

Rincón, C. (2015). La práctica docente y su relación con el conocimiento matemático temprano. Universidad del norte, Atlántico. Barranquilla: Maestria en educación.

Romero Acosta, J. L., Bonilla Pérez, G. A., & Álvarez Tamayo, O. D. (10, 11 Y 12 de Octubre de 2018). Las representaciones múltiples como estrategia didáctica para el fortalecimiento de la competencia argumentativa en básica secundaria. Revista Tecné, Episteme y Didaxis. Memorias, Octavo Congreso Internacional de formación de , 1-10.

Rojas Jiménez, D. E., & Valdivieso Colmenares, M. A. (2017). Diseño y aplicación de una secuencia didáctica en torno a prácticas experimentales desde física y química para el desarrollo de la argumentación basada en pruebas. Universidad Distrital Francisco José De Caldas, Cundinamarca. Bogotá: Facultad de ciencias y educación.

Ruiz- Higueras, L. (1994). Concepciones de los alumnos de secundaria sobre la noción de función. Análisis epistemológico y didáctico. Universidad de Granada. Granada, España: Departamento de Didáctica de las Matemáticas .

SEP. (2009). Plan de esrudios. Educación básica primaria. México, D.F.: SEP.

Schoenfeld, A. H. (1985). Mathematical problem solving. Calfornia: Academic press.

Solar Bezmalinovic, H. (2018). Implicaciones de la argumentación en el aula de matemáticas. Revista Colombiana de Educación (74), 155-176.

Solar Bezmalinovic, H., & Deulofeu Piquet, J. (2016). Condiciones para promover el desarrollo de la competencia de argumentación en el aula de matemáticas. Bolema: Boletim de Educación Matemática , 30 (56), 1092 - 1112.

Solar Bezmalinovic, H., & Deulofeu Piquet, J. (2014). Tratamiento de la contingencia desde el desarrollo de la competencia de argumentación en el aula de matemáticas. Acta Latinoamericana de Matemática Educativa , 317-325.

Soto Restrepo, J. F. (2018). La mayéutica como estrategia didáctica para la argumentación en el aula de clase. Universidad Autónoma de Manizales, Caldas. Manizales: Facultad de estudios sociales empreariales.

Stein, N. L., & Albro, E. R. (2001). The Origins and Nature of Arguments: Studies in Conflict Understanding, Emotion, and Negotiation, Discourse Processes. Journal Discourse Processes , 32 (2-3), 113-133 DOI: 10.1080/0163853X.2001.9651594.

Stein, N., & Bernas, R. (1999). The early emergence of argumentative knowledge skills (Vol. Vol. 5. Foundations of argumentative text processing). Amsterdam: Amsterdam University Press: En G. Rijlaarsdam & E. Espéret & J. Andriessen & P. Coirier Studies in writing.

Valbuena Duarte, S., Paternina Córdoba, y., & Cervantes Barraza, J. (2019). Argumentos de estudiantes de primaria en el contexto del álgebra temprana. Educación y Humanismo , 21 (37), 120-138 https://doi.org/10.17081/eduhum.21.37.3459.

Velásquez Torres, A. O. (2018). Niveles argumentativos y representaciones de los estudiantes sobre disoluciones químicas. Universidad autónoma de Manizales, Caldas. Manizales: Facultad de estudios sociales y empresariales.

Villella, J. (2004). Didáctica de la matemática. Buenos Aires: Jorge Baudino Ediciones.

Weston, A. (2006). Las claves de la argumentación (onceava ed.). Barcelona, España: Ariel S. A.

1. Docente Programa de Licenciatura en Matemática. Universidad del Atlántico. Colombia. Grupo de Investigación GIMED, Magister en Matemáticas, Magister en Educación y Dr(c). soniabalbuena@mail.uniatlantico.edu.co

2. Docente de básica primaria, maestrante en Educación. Atlántico. Universidad del Atlántico SUE -Caribe. luzelenamuni@gmail.com

3. Docente Programa de Licenciatura en Matemática. Universidad del Atlántico. Colombia. Grupo de Investigación GHEM. Universidad del Atlántico. Magister en Educación Matemática. jberriovalbuena@mail.uniatlantico.edu.co