ISSN 0798 1015

Vol. 41 (Nº 02) Año 2020. Pág. 4

El desarrollo del esquema de integral definida

The development of the defined integral scheme

ALDANA , Eliécer 1; GONZÁLEZ , María. T. 2; LÓPEZ-LEYTON , Cristhian 3

Recibido: 05/07/2019 • Aprobado: 17/12/2019 • Publicado 31/01/2020

Contenido

1. Introducción

2. Metodología

3. Resultados

4. Conclusiones

Referencias bibliográficas

1. Introducción

El estudio de la comprensión de los conceptos matemáticos es un campo de interés para la investigación en Educación Matemática, por tanto, este artículo de investigación hace parte de un estudio doctoral más amplio, y tiene como objetivo estudiar el desarrollo del esquema del concepto de Integral Definida. El ámbito del estudio es en la línea de Didáctica del Análisis Matemático y en el Pensamiento Matemático Avanzado (PMA) (Aldana, 2011). La comprensión para Dreyfus (1991) es un proceso que tiene lugar en la mente del estudiante y es el resultado de una larga secuencia de actividades de aprendizaje durante las cuales ocurren e interactúan una gran cantidad de procesos mentales.  Al respecto, otros investigadores (Mundy, 1984¸Ordaz, 2007; Guzmán, 1998; Cerizola, Pérez y Martínez, 2000¸ Colin y Lázaro, 2009), (citado por Aldana y González, 2016, p. 9) han señalado las dificultades que tienen los estudiantes con el aprendizaje y la comprensión del concepto de integral definida porque en muchos casos, no poseen los conceptos previos. Asimismo, Contreras y Lourdes (2006) analizaron las dificultades de comprensión de los estudiantes en este concepto producto de la enseñanza, porque tiene una implicación del objeto matemático límite, y como consecuencia de esto, el uso excesivo de la integral definida como un proceso de algoritmización del cálculo, ha conducido a un sentido algebraico del concepto lejano de su interpretación como resultado de procesos de cambio. Otros estudios muestran las concepciones de los profesores sobre la resolución de problemas en la enseñanza del Cálculo Integral (López-Leyton, Aldana y Erazo, 2019).

Por su parte, Boigues; Llinares y Estruch, (2010, p. 257) señalan que la comprensión de la integral definida encierra múltiples objetos que van más allá de una mera definición formal como diferenciar el objeto matemático de integral definida de su representación, de relacionar una sucesión y límite con la de suma de Riemann que vaya más allá de lo procedimental y considerarla como concepto dinámico que incluye nuevos elementos. Además, Schneider (1988), muestra las dificultades de los estudiantes en cuanto al teorema fundamental del cálculo integral. A partir de estas dificultades y de los mecanismos de construcción del concepto han realizado diferentes propuestas de enseñanza del concepto de Integral como la de Turégano (1994) que propone enseñarla utilizando la génesis histórica del concepto, comenzado con el concepto de integral de forma independiente de la diferenciación y como primera introducción al límite (Aldana, 2010).

De otra parte, Orton (1983) plantea que los alumnos realizan cálculos algebraicos en los que intervienen las integrales, pero no comprenden el papel que juega el límite en la definición de este concepto. Mundy (1984) presenta un cuestionario en el que los alumnos debían evaluar integrales como  pero obtuvo un número muy reducido de respuestas correctas. Rasslan y Tall (2002), exploran la imagen del concepto (Vinner, 1991) de Integral Definida con estudiantes de bachillerato mediante un cuestionario. Otros como Czarnocha et al. (2001) consideran la coordinación entre el esquema visual de la suma de Riemann y el esquema de los límites de la secuencia numérica para el desarrollo de una comprensión del concepto de Integral Definida. Desde lo epistemológico del concepto de integral y, de matemáticos como Cavalieri, Wallis y Roberval, Dubinsky, et al. (2000) diseñan una instrucción para estudiantes universitarios y concluyen que muestran una visión diferente que la desarrollada por la instrucción habitual. Depool (2004) utiliza tecnologías para desarrollar la comprensión del concepto de Integral Definida de estudiantes universitarios y definen un modelo de competencia cognitivo del concepto. Asimismo, Camacho et al. (2008), utilizan software en un curso de ingeniería para ayudar a los alumnos a comprender los conceptos de partición, refinamiento, aproximación y límite. Mediante una ingeniería didáctica, González-Martín (2006) trata de mejorar la comprensión de este concepto de integral impropia de estudiantes en los primeros cursos universitarios.

En cuanto al uso de manuales, Labraña (2001) afirma que: 1. los aspectos teóricos que se exponen en los manuales son poco comprensible para los estudiantes; 2. Hay un sesgo al considerar la integración como el cálculo de áreas, e incluso se llega a centrar en los cálculos aritméticos de suma y resta sin relacionarlos con el área; 3. El cálculo con primitivas ocupa un papel relevante, relegando el concepto de integral definida a un valor testimonial. Al respecto, Godino (2002) considera el análisis de manuales como una técnica que permite un estudio detallado de la actividad matemática, aportando una explicación a fenómenos didácticos que suelen darse en el aula desde diversos marcos teóricos. En Cantoral (2000), desde la construcción social del PMA, analiza la introducción de la integral definida en diversos momentos históricos, según el enfoque teórico previsto, con lo cual distingue la integral de Cauchy-Riemann, la de Newton-Leibniz y la de Wallis, y señala: “Cada una de las tres representaciones se ve acompañada de explicaciones diferentes. La primera alude a la aproximación, la segunda a la de acumulación y la tercera a la noción de promedio”.

La Comprensión del Concepto de Integral Definida tiene que ver con el PMA propio de las Matemáticas superiores que se enseñan y se aprenden en los últimos años de bachillerato y en el ámbito universitario, y que según Azcárate y Camacho (2003), este tipo de pensamiento posee unos procesos característicos como la abstracción, formalización del conocimiento, la representación, definición de los conceptos y la demostración, y los estudios de Piaget y García (1982) han sido la base para estudios en PMA. La teoría APOE utilizada en este estudio se conoce en inglés como APOS de Action, Process, Object, Schema y ha sido desarrollada por Dubinsky (1991; 2000) quien afirma que el origen de la teoría APOE se encuentra en la reformulación de la teoría Piagetiana de la Abstracción Reflexiva para el PMA. Piaget y García (1982, p. 10) definen la abstracción reflexiva, como “el mecanismo por el cual el individuo se mueve de un nivel a otro”, y permite establecer posibles subniveles de progresión de los estudiantes como el caso particular de este estudio. En Trigueros (2005, p. 9) “El mecanismo para pasar de un nivel a otro siempre es la abstracción reflexiva, por el razonamiento que hace el sujeto sobre el significado de las operaciones que realiza sobre el objeto matemático y de los resultados que produce en el propio sujeto”. La terna de los niveles: Intra, Inter y Trans en este artículo permiten una comprensión de desarrollo de los esquemas (Dubinsky y MacDonalds, 2001). DeVries (2001), adapta los niveles de un esquema así: Nivel intra, son aspectos individuales aislados de ciertas acciones, procesos y objetos de naturaleza similar. Por ejemplo, un sujeto entiende el concepto de integral definida a nivel intra, cuando no establece relaciones lógicas entre los elementos matemáticos, porque los recuerda de manera aislada, muestra concepciones erróneas en el uso de algunos elementos y establece sólo un intento de conjunción lógica entre ellos. Nivel inter, es la construcción de relaciones entre acciones, procesos y objetos. En el concepto de integral definida, el estudiante tiene un pensamiento a nivel inter, porque comienza a establecer relaciones lógicas entre los elementos matemáticos, especialmente la conjunción lógica entre los elementos cambiando de sistema de representación, establece la conjunción lógica, y la condicional, y aparecen los primeros intentos de síntesis entre sistemas de representación gráfico, algebraico y analítico. Nivel Trans, es una estructura completa en la cual las relaciones manifiestas en el nivel inter son comprendidas y dan coherencia al esquema. Esta investigación concibe que un estudiante manifiesta un nivel Trans de desarrollo del esquema de integral definida, cuando establece varias relaciones lógicas (conjunción, condicional y contrarrecíproco) entre elementos matemáticos de forma gráfica, algebraica y analítica, utiliza elementos necesarios en la resolución de tareas usando significados implícitos, toma decisiones, y establece síntesis en diversos sistemas de representación.

Este artículo hace parte de un estudio más amplio a nivel doctoral, en una perspectiva de investigación cualitativa orientada a la comprensión, cuyo objetivo es describir e interpretar la realidad educativa desde dentro” (Dorio, I., Massot, I. y Sabariego, M., 2009, p. 281). Es un estudio de casos, que “involucra aspectos descriptivos y explicativos de los temas objeto de estudio” (Bernal, 2006, p. 116). Los partícipes fueron estudiantes colombianos de tercer año de Licenciatura en Matemáticas con edades entre 18 y 28 años.

Los instrumentos utilizados para recoger los datos fueron: un cuestionario de ocho preguntas, teniendo en cuenta los elementos matemáticos del concepto de integral definida, a partir de un análisis previo del cuestionario aplicado y las de los estudiantes, se diseñó un guion de entrevista semiestructurada. Terminada la entrevista el investigador aplicó un mapa conceptual con el propósito de conocer la imagen mental del concepto. El diseño de la investigación tuvo varias fases: Fase 1: Planeación de la investigación, búsqueda en la literatura para formular un problema de investigación, asociado a unos objetivos y a unas preguntas ¿Cómo podemos caracterizar los niveles de desarrollo del esquema de Integral Definida? ¿Qué relaciones y qué elementos matemáticos se manifiestan en cada nivel de desarrollo de la Integral Definida? ¿Cómo podemos caracterizar el paso de un nivel de desarrollo al siguiente? luego un análisis del concepto de Integral Definida en los libros de texto, para determinar los elementos matemáticos que configuran el concepto para realizar una descomposición genética. Para ello, fue necesario entender los aspectos conceptuales: Los elementos matemáticos como una descomposición de los elementos constitutivos del Concepto de Integral Definida, asociada a toda la estructura matemática. Aquí, al igual que en Sánchez-Matamoros (2004) se habla de colección de elementos matemáticos que configuran el concepto matemático: El área como aproximación (ACA), El área como límite de una suma (ALS), La Integral Definida (LID), Las propiedades de la Integral Definida (PID), Los teoremas fundamentales y del valor medio (TFV). Las relaciones lógicas, establecidas entre los elementos matemáticos fueron:

Conjunción lógica ; Condicional  ;

Contrarrecíproco

Los sistemas de representación, las notaciones gráficas, algebraicas y analíticas, o declaraciones verbales, que expresan los conceptos y procedimientos, así como características y propiedades. Estas representaciones son utilizadas generalmente en la comprensión del concepto desde un sistema gráfico (G), algebraico (A) y analítico (AN). La descomposición genética del concepto de integral definida desde los elementos matemáticos del concepto de Integral Definida (DeVries, 2001), como el primer paso del análisis teórico de un concepto matemático en término de las construcciones mentales que un estudiante hace para desarrollar la comprensión del concepto. Fase 2: Diseño, aplicación y análisis de instrumentos, elaboración y validación de un cuestionario definitivo a partir de los ajustes a un precuestionario. Mediante un análisis previo del cuestionario se diseñó un guión de entrevista semiestructurada y finalmente un mapa conceptual (Huerta, Galán y Granel, 2000) para conocer la imagen del concepto. Fase 3: Triangulación de los instrumentos aplicados (cuestionario, una entrevista semiestructurada y un mapa conceptual), a partir de la información se analizan los tres instrumentos de acuerdo con (Cohen y Manion, 2002), para la obtención de resultados y de esta manera inferir las conclusiones, y asignar a los estudiantes niveles de desarrollo del esquema de integral definida. Durante el procedimiento, los estudiantes y fueron informados, según el Código Ético de la American Psychological Association (APA), (Bisquerra y Sabariego, 2009).

El análisis de los datos se hizo en tres fases, en la primera, la revisión de las respuestas dadas por los estudiantes en el cuestionario para sistematizar categorías, transcripciones de entrevistas y determinación unidades de análisis, y la interpretación del concepto de Integral Definida en un mapa conceptual. En esta segunda fase, se analiza cada tarea de forma aislada mediante los elementos matemáticos gráficos, algebraicos y analíticos, y sus relaciones lógicas, utilizando de manera conjunta el cuestionario, la entrevista y el mapa conceptual, para caracterizar la comprensión del concepto desde la postura teórica APOE.  La tercera fase, presenta las tareas resueltas por los estudiantes, y el nivel de desarrollo del esquema del concepto congregado en los tres instrumentos.

Tabla 1
Niveles de desarrollo del esquema de Integral Definida

Fuente: Elaboración propia

Este artículo presenta los resultados del estudio general; pero con el propósito de validar estos hallazgos, se muestran algunas evidencias de las actuaciones de estudiantes que por la forma como resolvieron las tareas a la luz de las categorías establecidas propias de la teoría (Tabla 1), les fueron asignados los niveles de comprensión del desarrollo del esquema del concepto de Integral Definida. Para ello, la tarea siguiente aplicada a todos los estudiantes, pero que para efectos del presente manuscrito se han tomado episodios de las actuaciones de algunos estudiantes para su interpretación y análisis.

Tabla 2
Tarea 3 de cuestionario

Nivel intra. En este nivel, no establecen relaciones lógicas entre los elementos matemáticos que utilizan en los sistemas de representación gráfico y algebraico. Por ejemplo, en el siguiente protocolo correspondiente a la tarea 3, el estudiante (A6), establece un intento de conjunción lógica entre los elementos matemáticos “el área como aproximación” y “el área como límite de una suma”, porque utiliza particiones, traza rectángulos inscritos y recuerda las sumas de Riemann para aproximar el área y el proceso límite de una suma Riemann, pero no logra utilizar los dos elementos conjuntamente para resolver la tarea:

I: ¿Sabría comentarme como ha resuelto la tarea?

A6: … como el proceso límite de una suma de Riemann, que consiste en que cada partición épsilon la voy a evaluar en la función dada y la multiplico por la longitud del intervalo para conocer el valor de cada rectángulo, cuando calcule las áreas de cada uno de estos rectángulos, sumo esas particiones y obtengo una aproximación del área total.

I: ¿Cómo lo haría hasta obtener un valor aproximado?

E. Con rectángulos hallo el área como la base por la altura y luego las sumo.

En el protocolo establece un intento de conjunción lógica entre los elementos matemáticos “el área como aproximación”, “el área como límite de una suma” de forma gráfica, porque utiliza rectángulos inscritos al área bajo la curva para hacer una aproximación por defecto, de forma algebraica porque utiliza la fórmula del triángulo y analítica porque menciona particiones sumas de Riemann y el límite de la sumatoria Riemann. Pero está demostrado que estos elementos los recuerda de manera aislada, porque no logra utilizar los elementos necesarios; porque, aunque utiliza una aproximación del área por defecto obtiene un valor superior al valor real del área y cuando se le pide aproximar más el área menciona que podría hacer mayor número de particiones cada vez, pero no logra aplicar el elemento matemático “el área como límite de la una suma”.

Figura 1
A6 Resolución AN de la
tarea 3 del cuestionario

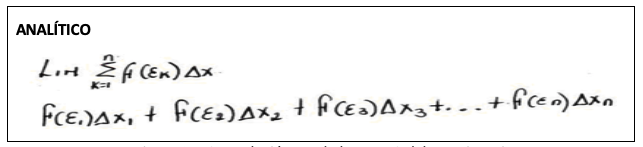
Utiliza el elemento matemático “el área como aproximación” de forma algebraica, porque plantea una suma de Riemann, y cuando utiliza el límite de la suma lo deja inconcluso.

Figura 2
A6 Resolución G de la
tarea 3 del cuestionario

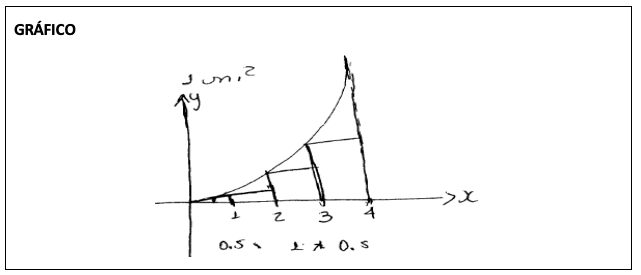
Aquí continúa utilizando “el área como aproximación” de forma gráfica, dibuja la función, hace 4 particiones, traza 5 rectángulos inscritos al área bajo la curva.

Figura 3
A6 Resolución A de la
tarea 3 del cuestionario

En la entrevista responde de forma algebraica utilizando particiones de 0.5 la primera y de 1 unidad de base las siguientes, y de altura la función evaluada en un , , calcula el área por defecto de cada rectángulo, suma las áreas aproximantes y obtiene un valor aproximado del área que aunque es por defecto es superior al valor real del área bajo la curva. En la resolución de la tarea establece un intento de conjunción lógica y utiliza mayor número de elementos matemáticos gráficos, algebraicos y analíticos, pero desconoce otros elementos necesarios que le permiten establecer conexiones en los procedimientos de resolución de la tarea.

Nivel ínter. En este nivel de desarrollo del esquema los estudiantes comienzan a establecer relaciones lógicas entre los elementos matemáticos que utilizan generalmente en los sistemas de representación gráfico, algebraico y analítico, siendo la conjunción lógica la relación que con más frecuencia aparece en los razonamientos, la “condicional lógica” es la que menos veces se presenta en los procedimientos de resolución de las tareas y el contrarrecíproco es una relación lógica que no se pone de manifiesto en este nivel. La conjunción lógica entre elementos matemáticos cambiando de sistema de representación, es la relación más frecuente entre los estudiantes y que no siempre la establecen de forma correcta. En el protocolo que corresponde a la tarea 3, se establece la conjunción lógica entre los elementos matemáticos gráficos y algebraicos: “El área como aproximación” y “el área como límite de una suma” de forma gráfica, algebraica y analítica.

A partir de estos dos elementos matemáticos utilizados conjuntamente puede resolver la tarea, porque infiere el valor aproximado del área y el valor exacto del área. Utiliza el elemento matemático “el área como aproximación”:

I: ¿Qué valor obtuvo al aproximar el área?

A9: 30 unidades de medida cuadrada.

I: ¿Qué ocurre con las sumas al escoger todos los subintervalos de la partición cada vez más pequeños?

A9: Que el valor que me da se va aproximando más al área que estoy buscando.

I: ¿Cuántos rectángulos podría trazar?

A9: En cualquier área podría trazar infinitos, hablando conceptualmente de lo que uno en matemáticas tiene como conceptos.

I: ¿Por qué ha utilizado este procedimiento?

A9: Porque es el que conocía por la explicación que nos dio el profesor de la sumatoria de Riemann y de lo que es el método exhaustivo.

Figura 4
A9 Resolución G de la
tarea 3 del cuestionario

Usa particiones, traza rectángulos para hacer una aproximación del área por exceso y plantea una sumatoria del área

Figura 5
A9 Resolución A de la
tarea 3 del cuestionario

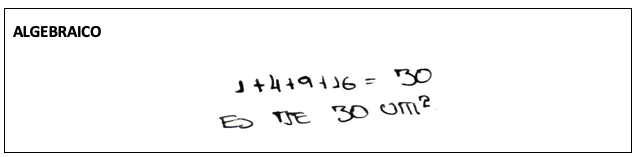
Utiliza de forma algebraica la fórmula del área del rectángulo, toma particiones de una unidad de base, evalúa la función en cada subintervalo para hallar la altura, calcula el área de cada rectángulo, suma las áreas y obtiene el área aproximada por exceso. Aplica “el área como aproximación”, porque traza rectángulos, usa particiones, aplica la fórmula del área del rectángulo, afirma que entre más rectángulos trace, se aproxima más al área y obtiene un valor aproximado por exceso de 30 unidades cuadradas. Utiliza el elemento matemático analítico “el área como límite de una suma”:

I: ¿De qué otra forma diferente a la anterior podría calcular el área bajo la gráfica?

A9: Usando el límite de la sumatoria de Riemann, que en últimas es una Integral Definida.

I: ¿Cómo plantearía el límite de una sumatoria de Riemann en este ejercicio?

A9: Es que el límite de la sumatoria de Riemann cuando tiende a infinito y la partición tiende a   siempre es la Integral Definida, pero lo haría con la Integral Definida.

I: ¿Cómo plantea con esta función el límite de una sumatoria de Riemann?

A9: Es que por propiedad transitiva si A es igual a B y B es igual a C pues A tiene que ser igual a C, o sea, si el límite de la sumatoria de Riemann, es una Integral Definida, pero sería el límite cuando la partición tiende a cero y tiende a infinito de la sumatoria.

Figura 6
A9 Resolución AN de la
tarea 3 del cuestionario

En el protocolo establece una conexión entre “el área como aproximación” porque menciona las particiones, la construcción de rectángulos inscritos y afirma que si traza rectángulos cada vez de menor longitud en la base, se aproxima más a la curva y el elemento matemático analítico “el área como límite de una suma”, aunque el cálculo del área es incorrecto, conecta estos criterios con el límite de las sumas Riemann obtenidas de las áreas aproximadas de los rectángulos y además asegura que cuando está calculando el límite de la sumatoria lo que está aplicando es la Integral Definida. Durante la resolución de la tarea se pone de manifiesto que establece “conjunción lógica” entre los elementos matemáticos “el área como aproximación” y “el área como límite de una suma Riemann”, y “la Integral Definida” y un comienzo de síntesis de los sistemas de representación gráfico, algebraico y analítico, por lo que hace con los elementos que conoce en la resolución de la tarea.

Nivel trans. Este nivel de desarrollo del esquema se caracteriza porque los estudiantes que establecen varias relaciones lógicas (conjunción, condicional y contrarrecíproco) de forma correcta entre los elementos matemáticos gráficos, algebraicos y analíticos que utilizan en la resolución de las tareas. Esta categoría corresponde a la misma tarea 3, el alumno A11, utiliza los elementos matemáticos gráfico, algebraico y analítico: “El área como aproximación”, “el área como límite de una suma”, “la Integral Definida” y el teorema fundamental”:

En este nivel de desarrollo del esquema ellos establecen una síntesis de los sistemas de representación, gráfico, algebraico y analítico:

I: ¿Sabría comentarme cómo ha resuelto la tarea?

A11: … entiendo por partición coger un intervalo y dividirlo en un conjunto de   puntos, mayores que el extremo izquierdo, pero menores que el extremo derecho del intervalo, y que todos estos valores eran mayores que “a”, que en este caso era cero, que era el extremo izquierdo del intervalo y que todos esos puntos eran menores que “b”, eso es lo que entendía como particionar, por comodidad tuve en cuenta una partición regular, que es que la longitud de cada intervalo sea la misma.

Figura 7
A9 Resolución AN de la
tarea 3 del cuestionario

En el protocolo utiliza el elemento matemático gráfico y algebraico “el área como aproximación”, porque utiliza el esquema general de aproximación y traza rectángulos circunscritos para aproximar el área por exceso.

I: ¿Qué es una suma de Riemann?

A11: …entiendo que es particionar y sumar las áreas en unos rectangulitos al tomar todas esas áreas, eso es lo que llamo una suma de Riemann y el límite es cuando hago que esa longitud sea cada vez más pequeña y tienda a cero, es lo que llamamos Integral Definida.

I: ¿Cómo concluye su respuesta?

A11: Lo que hice aquí fue aplicar la definición matemática de la Integral Definida, que se define como el límite de una suma de Riemann, ahí lo escribí y cogía la función y tomaba un   cualquiera, quien era ese  , era cualquier punto que estaba en cualquier intervalo, en cualquier parte del intervalo lo que hacía era coger ese punto que lo llame   y lo evalué en la función y lo multiplique por la altura, de cada rectángulo, que en ese caso lo llame   y al hacer esa suma obtuve el valor de la integra definida.  

Figura 8
A11 Resolución A y AN de
la tarea 3 del cuestionario

Además, cuando piensa en el significado matemático de la Integral Definida lo asocia con el límite de una suma de Riemann. Establece relación entre los elementos matemáticos el área como aproximación y la Integral Definida, porque demuestra que tiene encapsulado el concepto de área como una aproximación y el concepto de área como una Integral Definida. En la resolución de la tarea se evidencia que establece una “conjunción lógica” entre los elementos matemáticos gráficos, algebraicos y analíticos “el área como aproximación” y “el área como límite de una suma”, porque utiliza dos elementos matemáticos para calcular el valor del área y utiliza la condicional lógica cuando infiere que los rectángulos se hacen cada vez más pequeños, entonces el número de particiones, tiende a infinito. Establece una relación entre la representación gráfica y los sistemas de representación algebraico y analítico de los elementos matemáticos “el área como aproximación” y “el área como límite de una suma”, utiliza el esquema general de aproximación del área, calcula las sumas de Riemann y establece una conexión con el límite de la suma para dar el valor del área. Establece una síntesis de los sistemas de representación gráfico, algebraico y analítico; aunque responde de forma correcta, no se puede precisar que haya tematizado el esquema del concepto.

Por la forma como los estudiantes resuelven la tarea, a la luz de la caracterización del marco teórico establecido, permitió asignarles de manera progresiva y continua un subnivel y nivel de desarrollo del esquema del concepto de Integral como se ponen en evidencia.

Tabla 3
Caracterización de los niveles de desarrollo del esquema de Integral Definida

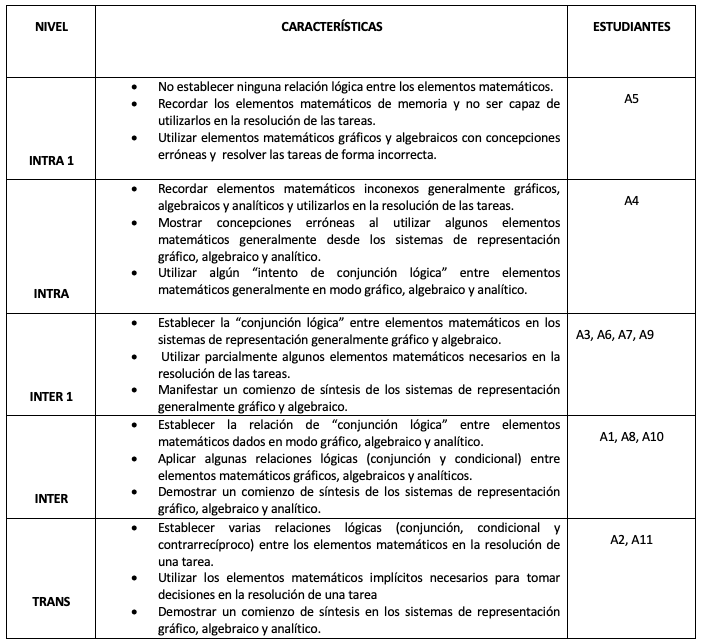
Fuente: Elaboración propia

-----

Tabla 4
Relaciones Lógicas y Elementos Matemáticos que Caracterizan
el Desarrollo del Esquema de Integral Definida

Fuente: Elaboración propia

Los instrumentos teóricos y metodológicos permitieron comprender que la construcción del conocimiento es progresivo y continuo, y el paso de un nivel al siguiente se instaura por las relaciones lógicas que un estudiante establece entre los elementos matemáticos que conoce y cómo los utiliza para resolver las tareas propuestas. 

Los primeros intentos por establecer relaciones lógicas entre elementos matemáticos son la “conjunción lógica”, siendo éste el primer tipo de relación lógica que de forma frecuente y correcta crean los estudiantes, la “condicional lógica” es otra relación, pero menos común entre ellos, y la relación del “contrarrecíproco”, sólo esta manifiesta en algunos estudiantes.

Los elementos matemáticos en general son los mismos, aunque varían de un estudiante a otro por la forma cómo los usan, y los que comúnmente recuerdan son “el área como aproximación”, “la Integral Definida” y “el teorema fundamental”, y los que menos “las propiedades de la integral” y especialmente “el área como límite de una suma”, y algunos son recordados de forma incorrecta y/o con concepciones erróneas.

En el subnivel INTRA 1, de desarrollo del esquema no se produce conjunción lógica, los primeros intentos por establecer conjunción lógica se ponen de manifiesto en el nivel INTRA,  la aparición de la “conjunción lógica” se establece a partir del subnivel INTER 1 y la evidencia tanto de la conjunción lógica como de la condicional es propio del nivel INTER y del nivel TRANS, y la relación del contrarrecíproco, sólo se encuentra en aquellos estudiantes que fueron asignados al nivel TRANS de desarrollo del esquema. El subnivel de desarrollo que predomina en los estudiantes es el INTER 1. Así mismo, aunque en el subnivel INTRA 1, hay privilegio del registro gráfico y algebraico, la construcción progresiva de los subniveles de desarrollo del esquema no depende de los sistemas de representación gráfico, algebraico y analítico a excepción del nivel TRANS, de desarrollo el cual establece la síntesis en los sistemas de representación gráfico, algebraico y analítico.

Aldana, E., y González, Astudillo, M. T. (2010). Comprensión del concepto de integral definida, el caso de un alumno universitario. Revista de investigaciones, Universidad del Quindío, (1).

Aldana, E. (2011). Comprensión del concepto de integral definida en el marco de la teoría “APOE”. TesisDoctoral. Universidad de Salamanca, España.

Aldana, E., y González, Astudillo, M. T. (2016). La función valor absoluto y el desarrollo del esquema de la integral definida. Revista Electrónica de Investigación en Educación en Ciencias, 11, (1).

Azcárate, C. y Camacho, M. (2003). Sobre la Investigación en Didáctica del Análisis Matemático. Boletín de la Asociación Matemática Venezolana, 10, 2, 135-149.

Bernal, C. A. (2006). Metodología de la Investigación (2ª ed.). México: Prentice Hall.

Bisquerra, R. y Sabariego, M. (2009). El Proceso de Investigación (Parte 1). En R. Bisquerra (Coord.). Metodología de la Investigación Educativa (2ª ed.). (89-125). Madrid: La Muralla.

Cantoral, R. (2000). Sobre la construcción social del conocimiento matemático avanzado. Documento interno del Cinvestav, pp. 1-4.

Camacho, M., Depool, R. y Sabrina, G. (2008). Integral Definida en diversos contextos. Un estudio de casos. Educación Matemática, 20, 3, 32-57.

Cerizola, N., Pérez, N., y Martínez, R. (2000). Una noción matemática básica y aparentemente simple: el valor absoluto de un número real. Actas de la XIIIReunión Latinoamericana de MatemáticaEducativa. Editor CLAME.

Cohen, M.  y Manion, L. (2002). Métodos de Investigación Educativa (2ª ed.). Madrid: La Muralla.

Colín, M. P., y Lázaro, L. (2009). El valor absoluto en el nivel básico. Su uso en el contexto aritmético. XCongreso Nacional de Investigación Educativa.

Contreras y Lourdes (2006, p. 77). Complejidad ontosemiótico de un texto sobre la introducción a la integral definida. Relime, 9 (1), 65-84

Czarnocha, B., Loch, S., Prabhu, V. y Vidakovic, D. (2001). El Concept of definite integral: Coordination of two Schemas. En María van den Heuvel – Penhuizen (Ed.). Proceedings of the XXV Conference of the International Group of Mathematics Education (pp. 12 – 17). Utrecht: Freudenthal Institute.

Depool, R. A. (2004). La Enseñanza y Aprendizaje del Cálculo Integral en un Entorno Computacional. Actitudes de los Estudiantes Hacia el uso de un Programa de Cálculo Simbólico (PCS). Tesis Doctoral. Universidad de La Laguna.

DeVries, D. J. (2001). RUMEC / APOS Theory Glossary. Georgia Collage & State University. Milledgeville.http://www.cs.gsu.edu/~rumec/Papers/glossary.html. [Disponible el 18 de agosto de 2008]

Dorio, I., Massot, I. y Sabariego, M. (2009). Características Generales de la Metodología Cualitativa. En R. Bisquerra (Coord.). Metodología de la Investigación Educativa (2ª ed.). (275-292). Madrid: La Muralla. S.A.

Dreyfus, T. (1991). Advanced in Mathematical Thinking Processes. En D. Tall. (Ed.). Advanced in Mathematical Thinking (pp.25–41). Boston: Kluwer Academic Publishers.

Dubinsky, E. (1991). Reflective Abstraction in Advanced Mathematical Thinking, En D. Tall. (Ed.). Advanced Mathematical Thinking (pp. 95-123).Dordrecht: Kluwer Academic Publishers.

Dubinsky, E. (2000). Using a Theory of Learning in College Mathematics Courses. Teaching and Learning Undergraduate Mathematics, Newslertter12. http://ltsn.mathstore.ac.uk/newsletter/may2001/pdf/learning.pdf.  [Disponible el 25 de agosto de 2008]

Dubinsky, E. y MacDonald, M. A. (2001). APOS: A Constructivist Theory of Learning in Undergraduated Mathematics Education Research. En D. Holton (Ed.), The teaching and Learning of Mathematics at University Level. An ICMI Study. 7 (pp.273- 280). Dordrecht: Kluwer Academia Publisher.

Godino, J. (2002). Un Enfoque Ontológico Semiótico de la Cognición Matemática. Recherches en Didactique des Mathématiques, 22, 2/3, 237-284.

González-Martín, A. S. (2006). La Generalización de la Integral Impropia desde las Perspectivas Numérica, Gráfica y Simbólica Utilizando Entornos Informáticos. Problemas de Enseñanza y Aprendizaje. Tesis Doctoral. Universidad de la Laguna.

Guzmán, I. (1998). Registros de representación, el aprendizaje de nociones relativas a funciones: voces de estudiantes. Revista Latinoamericana de Matemática Educativa. Relime, 1, 1, 5-21.

Huerta, M. P., Galán, E. y Granell, R. (2000). Concept Maps in Mathematics Education: A Possible Framework for Students’ Assessment. Ministerio de Educación Cultura y Deporte (Today Ministerio de Ciencia y Tecnología), 1-22.

Labraña, P. A. (2001). La avaliación das concepcións dos alumnos de COU e bacharelato acerca do significado do cálculo integral. Tesis de doctorado, Universidad de Santiago de Compostela, España.

López-Leyton, C., Aldana, E y Erazo, J. D. (2019). El papel de la resolución de problemas para la enseñanza del Cálculo Integral: Un estudio de caso. Revista Espacios. 40 (17), 8-21. Recuperado de: http://www.revistaespacios.com/a19v40n17/a19v40n17p12.pdf

Mundy, J. (1984). Analysis of Errors of First Year Calculus Students. En Bell, A., Low, B., y Kilpatrick, J., (Eds.). Theory Research and Practice in Mathematics Education. Proceedings, ICME 5. Adelaide, Working group reports and collected papers, Shell Center. Nottingham. 170-172.

Ordaz, M. G. (2007). Las secuencias didácticas con enfoque constructivista: el caso de la función valor absoluto. Acta Latinoamericana de Matemática Educativa, (Vol. 20). CLAME.

Orton, A. (1983). Students` Understanding of Integration. Educational Studies in Mathematics. D. Rediel Publishing Company. Dordrecht: Holland/Boston: U.S.A. 14, (1), 1 – 18.

Piaget, J., y García, R. (1982). Psicogénesis e Historia de la Ciencia. México, España, Argentina, Colombia. (Madrid): Siglo XXI.

Rasslan, S. y TalL, D. (2002). Definitions and Images for the Definite Integral Concept. Proceedings of the 26th PME. 4, 89-96.

Sabariego, M. (2009). La Investigación Educativa: Génesis, Evolución y Características. En R. Bisquerra (Coord.). Metodología de la Investigación Educativa (2ª ed.). (50-87). Madrid: La Muralla.

Sánchez-Matamoros, G. M. (2004). Análisis de la Comprensión en los Alumnos de Bachillerato y Primer año de Universidad sobre la Noción de Derivada (desarrollo del concepto). Tesis Doctoral. Universidad de Sevilla.

Schneider, M. (1988). Des objets mentaux “aire” et “volume” au calcul des primitives. Tesis de doctorado, Universidad Católica de Lovaina, Bélgica

Tall, D. (1991). Reflections on APOS theory in Elementary and Advanced Mathematical Thinking. En O. Zaslavsky (Ed.), Proceedings of the XXIII Conference for the Psychology of Mathematics Education, 1, (pp. 111 – 118). Haifa.

Turégano, P. (1994). Los Conceptos en Torno a la Medida y el Aprendizaje del Cálculo Infinitesimal. Tesis Doctoral. Universitat De València.

Trigueros, M. (2005). La Noción de Esquema en la Investigación en Matemática Educativa a Nivel Superior. Educación matemática, 17, 1, 5-31.

Vinner, S. (1991). The Rol of Definitions in the Teaching and Learning of Mathematics. En D. Tall. (Ed.). Advanced Mathematical Thinking, 66-81. Dordrecht: Kluwer Academic Publishers

1. Doctor en Educación Matemática, Universidad de Salamanca, España. Líder del grupo de investigación GEMAUQ. Filiación: Profesor Investigador Universidad del Quindío. Contacto: eliecerab@uniquindio.edu.co. Orcid: https://orcid.org/0000-0003-1691-2699

2. Doctora en Educación Matemática, Universidad de Salamanca, España. Filiación: Universidad de Salamanca. Contacto: maite@usal.es. CVN:https://mtskweb.files.wordpress.com/2018/06/cvn_ip_2017-marc3ada-teresa-gonzc3a1lez-astudillo.pdf

3. Maestría en Ciencias de la Educación, Universidad del Quindío. Licenciado en Matemáticas, Universidad del Quindío. Profesor investigador, adscrito al grupo de investigación GEMAUQ. Orcid: https://orcid.org/0000-0001-7335-2339