ISSN 0798 1015

Vol. 40 (Nº 33) Año 2019. Pág. 10

Estrategias en la resolución de problemas de división-medida por estudiantes de séptimo básico en Chile

Strategies in the solving of division-measure problems by seventh grade students in Chile

MÁRQUEZ T., Maximina 1; ARREDONDO, Elizabeth H. 2 y GARCÍA-GARCÍA, Jaime I. 3

Recibido: 30/052019 • Aprobado: 12/09/2019 • Publicado 30/09/2019

Contenido

1. Introducción

2. Una aproximación a los problemas de isomorfismo de medidas

3. Algunas investigaciones sobre problemas de estructura multiplicativa

4. Metodología

5. Resultados

6. Discusión y conclusión

Referencias bibliográficas

1. Introducción

Actualmente, la resolución de problemas es considerada una competencia fundamental en la Educación Básica en Chile. Al respecto, las Bases Curriculares del 2013 sugieren a los profesores brindar oportunidades a sus estudiantes para desarrollar esta competencia, poniendo en práctica estrategias de resolución que apoyen la comprensión, planificación, acción y comprobación de resultados, y puedan ser utilizadas en diversas situaciones (MINEDUC, 2013).  Estudios sobre esta temática en otros países han mostrado que los niños (10-12 años) se resisten a utilizar estrategias alternativas para resolver problemas de isomorfismo de medidas, después de conocer el algoritmo de la división (Ivars y Fernández, 2016).

La necesidad de profundizar sobre la enseñanza y el aprendizaje de división-medida se justifica, según se describe en algunas investigaciones, por las dificultades que presentan los estudiantes ante este tipo de problemas; por ejemplo, las limitaciones que se han observado en los estudiantes para asociar el enunciado del problema con la operación de división para resolverlo.

Asimismo, la investigación enfocada en la resolución de problemas de isomorfismo de medidas por parte de los estudiantes es de gran importancia, ya que este tipo de problemas aparecen en la mayoría de las actividades desarrolladas al trabajar la multiplicación en la Educación Básica en Chile, y en niveles educativos superiores, ratificando su presencia permanente en el currículo a lo largo de la escolaridad.

Este trabajo, que forma parte de un proyecto de investigación longitudinal desarrollado en la Universidad de los Lagos, tiene como objetivo caracterizar las estrategias que presentan los estudiantes de séptimo básico cuando resuelven problemas de estructura multiplicativa; en este sentido, nos centramos en las maneras que ellos resuelven problemas de isomorfismo de medidas, específicamente problemas de división-medida. Además, los resultados de este estudio sirven de preámbulo para el diseño de una formación para futuros profesores de Educación Básica en la enseñanza-aprendizaje de la resolución de problemas matemáticos, centrada en las estrategias utilizadas por estudiantes.

En líneas generales, los problemas de estructura multiplicativa son aquellas situaciones matemáticas cuyo tratamiento implica la realización de alguna multiplicación, división o una combinación de esas operaciones (Vergnaud, 1997). Existe un consenso general en clasificar los problemas de estructura multiplicativa en tres grandes clases: isomorfismo de medidas, producto de medidas y problemas con un espacio de medida (Vergnaud, 1997). La primera clase, isomorfismo de medidas, comporta una estructura que engloba problemas de proporcionalidad simple directa entre dos magnitudes M1 y M2 y pone en juego cuatro cantidades, de las cuales, en problemas más simples, una de éstas es 1. Dependiendo de cuál cantidad representa la incógnita en el problema, se tienen tres grandes tipos de problemas de isomorfismo de medidas: multiplicación, división-medida (búsqueda de la cantidad de unidades) y división-partitiva (búsqueda del valor unitario). En la Figura 1 se muestra la tabla de correspondencia entre las dos magnitudes en estos tipos de problemas.

Figura 1
Tabla de correspondencia entre magnitudes
en problemas de isomorfismos de medidas

(Vergnaud, 1997, pp. 218-219)

Dos aspectos que destacan en la investigación sobre problemas de estructura multiplicativa en clases de matemáticas se refieren a las dificultades que tienen los niños para resolver este tipo de problemas, y las estrategias empleadas por ellos en su resolución. A continuación, describiremos brevemente algunas de ellas.

3.1. Dificultades asociadas a problemas de estructura multiplicativa

La resolución de problemas de estructura multiplicativa engloba diversas dificultades manifestadas en las respuestas de los estudiantes a estas situaciones. Esto se debe principalmente a que los maestros suelen presentar a los alumnos el mismo tipo de problema, reproduciendo así su concepción acerca de la multiplicación en la planificación de la clase (García y Suárez, 2011). Algunos investigadores han centrado sus estudios en los procedimientos de los estudiantes al resolver problemas de estructura multiplicativa (Espinoza, Barbé y Gálvez, 2011; Gómez y Contreras, 2009; Llinares y Sánchez, 1998), tratando de indagar sobre las actuaciones cognitivas de estos sujetos ante un problema expresado en representación verbal, sobre las limitaciones en el desarrollo de un problema, entre otras cuestiones. Los resultados de estas investigaciones muestran errores, obstáculos y niveles de complejidad analizados desde las producciones de los niños de diferentes grados de escolaridad.

También se ha indagado sobre las dificultades de los estudiantes en los problemas de división-medida. Al respecto, Lago, Rodríguez, Enesco, Jiménez y Dopico (2008) mostraron las dificultades que tuvieron estudiantes de primer grado de Educación Secundaria (12 años) en la realización de problemas no-rutinarios de división con resto distinto de cero. Los estudiantes emplearon algoritmos mecánicamente sin considerar aspectos realistas. Se presentaron a los estudiantes problemas tanto de división-partitiva como de división-medida con cuatro tipos de resto: resto no divisible, resto divisible, resto como resultado y reajustar el cociente. Los resultados mostraron que los estudiantes tuvieron mayor éxito de resolución en los problemas de división-partitiva y presentaron mayor dificultad cuando realizaron problemas de división-medida, aunque aplicaban correctamente el algoritmo de resolución, no consideraron aspectos fundamentales del enunciado y algunos errores presentes fueron el no incrementar el cociente para reajustarlo, o responder con el cociente en lugar del resto.

Li y Silver (2000) encontraron que, en problemas de división con resto distinto de cero en donde se debe añadir una unidad al cociente entero o redondear por exceso un cociente decimal para dar la respuesta, los estudiantes que usaron una estrategia “arraigada en el contexto” tuvieron mayor éxito de resolución que los que utilizaron el algoritmo de la división; esto fue debido a que los métodos alternativos utilizados en la resolución del problema les permitieron superar las dificultades inherentes a la interpretar el resto.

En un estudio sobre la evolución de niveles de éxito en problemas de estructuras multiplicativas, Ivars y Fernández (2016) evidenciaron que los niños de 10-12 años se resisten a usar estrategias alternativas para resolver problemas de estructura multiplicativa y que el uso de algoritmos no implicó una disminución de las estrategias incorrectas, alcanzando un nivel de éxito que puede considerarse de dificultad alta. Al parecer, la introducción del algoritmo en la resolución de problemas multiplicativos en estos niños conlleva la disminución del uso de otras estrategias correctas que implican una comprensión adecuada de la situación, pero no conllevan una mejora en la comprensión de dichas situaciones.

3.2. Estrategias utilizadas en problemas de estructura multiplicativa

Diversos investigadores han identificado los tipos de estrategias que utilizan los estudiantes en los problemas de división-medida y su evolución a lo largo del tiempo. Algunos comienzan modelando con objetos o con dibujos, formando grupos de un número fijo de objetos y contando el número de grupos; luego utilizan el conteo: cuentan a saltos, sumando hasta alcanzar el número dado de objetos, o van restando desde el número dado de objetos hasta conseguir un número menor que el sustraendo; y finalmente usan operaciones como la multiplicación y la división (Downton, 2009; Li y Silver, 2000; Vergnaud, 1983).

Downton (2009) identificó ocho estrategias utilizadas por estudiantes de Educación Básica (8-9 años) sobre problemas de división-partitiva y división-medida, entre las que se destacan: a) confuso: utiliza el uso compartido o de uno a más grupos con materiales, dedos o dibujos y calcula el total por omisión o por conteo aditivos; b) modelado directo: utiliza el uso compartido o de uno a muchos grupos con materiales, dedos o dibujos y calcula el total por omisión o por conteo de aditivos; c) modelado parcial: estrategia que se apoya parcialmente en el modelado de la situación con materiales concretos o con dibujos. Utiliza también el conteo a saltos para hallar el total; d) adición o sustracción repetida: se suma el divisor repetidamente hasta alcanzar el dividendo, o se resta el divisor al dividendo repetidamente hasta llegar a cero o a una cantidad inferior al divisor; e) duplicar o reducir a la mitad: uso de dobles, duplicando el divisor o los resultados obtenidos hasta alcanzar el dividendo, o reducir a la mitad el dividendo y los resultados obtenidos hasta alcanzar el divisor.

Otras investigaciones aportan información sobre estrategias usadas por los estudiantes en problemas muy particulares; por ejemplo, en Lima y Carvalho (2013) se presentan cinco estrategias de resolución de 4 problemas de división-medida y división partitiva por niños con edades comprendidas entre 8 y 13 años: 1) algoritmo de la división, 2) estrategias combinadas, 3) algoritmo de la multiplicación, 4) estrategia personal (repetición aditiva, repetición sustractiva, hacer un dibujo o una simulación), y 5) lengua materna.

La metodología empleada en este estudio se enmarca dentro de un enfoque cualitativo, de tipo descriptivo e interpretativo, ya que se analizan las estrategias en la resolución de problemas de división-medida que presentan 100 estudiantes de séptimo básico de dos colegios en Chile, uno ubicado en la Región de los Ríos y otro en la Región de los Lagos, con edades comprendidas entre los 12-14 años.

4.1. Datos e instrumento de la investigación

Los datos de esta investigación provienen de las respuestas de los estudiantes a tres problemas de estructura multiplicativa, de isomorfismo de medida del tipo división-medida, incluidos en un instrumento de tipo cuestionario. Dichos problemas fueron seleccionados y modificados de otras investigaciones (Callejo y Vila, 2009; Verschaffel y De Corte, 1997), y pueden ser resueltos por medio de una división o por otros métodos alternativos.

Los problemas Postes de Luz y Albergue presentan características comunes, pues en estas situaciones las magnitudes son discretas y su resolución demanda que se añada una unidad al cociente de la división para formar con el resto un grupo más de postes de un color determinado (en el caso del primer problema) o de alumnos sentados en otra mesa (en el caso del segundo problema. En el problema Pasteles las magnitudes son continuas y para resolverlo es preciso interpretar el significado de la fracción que resulta de dividir un entero por una fracción para saber cuánto sobra. Los enunciados de los problemas son los siguientes:

• Postes de Luz. Para celebrar el quinto centenario de su pueblo, el alcalde decidió pintar de diferentes colores los postes de luz de la calle principal. Las tres primeras las pintaron de rojo, las tres siguientes de verde y las tres siguientes de azul, y así sucesivamente, sin repetir colores. Si se pintaron 35 postes de luz, ¿cuántos colores diferentes necesitó?
• Albergue. 103 estudiantes están en un albergue. Las mesas del comedor tienen 20 asientos y hay 15 mesas. Si van completando las mesas sin dejar asientos libres, ¿cuántas mesas ocuparan?
• Pasteles. Tengo cuatro pasteles. Quiero dar tres quintos de pastel a cada niño. ¿A cuántos niños puedo dar? ¿Qué me sobra?

4.2. Procedimiento de análisis de datos

Se analizaron las respuestas de los estudiantes considerando el éxito y las estrategias en la resolución de los problemas. En este trabajo consideramos como estrategias de resolución aquellos procedimientos que utiliza el estudiante para resolver el problema y llegar a una solución (correcta o incorrecta).

Con relación al éxito en la resolución del problema, se consideran como: a) respuestas correctas, aquellas que presentan procedimiento y solución correctos; b) respuestas regulares, aquellas que exhiben errores de cálculo o de precisión, pero muestran una comprensión de la relación entre las cantidades implicadas; y c) respuestas incorrectas, aquellas que presentan errores tanto en el procedimiento como en la solución. En cuanto a las estrategias de resolución, mediante triangulación de expertos, se realizó un análisis para identificar los procedimientos utilizados por los estudiantes para obtener la solución al problema; posteriormente, se crearon categorías cuyo concepto corresponde la estrategia en común: división (D), modelación-agrupamiento (MA), multiplicación (M), suma-resta repetida (SRR), conteo a saltos (CS), regla de tres (RT), uso de todos los datos (UTD) y combinación de estrategias (CE). Finalmente, se clasificó cada una de las respuestas de los estudiantes en las categorías establecidas.

A continuación, se describen cada una de las estrategias, y se ejemplifican con la respuesta dada por un estudiante.

División (D)

Consiste en utilizar el algoritmo de la división para la resolución del problema. En la Figura 2 se presenta esta estrategia utilizada por el estudiante E7 en el problema Postes de Luz.

Figura 2
Estrategia División

Modelización-Agrupamiento (MA)

Consiste en representar gráficamente las cantidades y agruparlas hasta llegar al total. En la Figura 3 se presenta esta estrategia utilizada por el estudiante E78 en el problema Pasteles.

Figura 3
Estrategia Modelización-agrupamiento

Multiplicación (M)

Consiste en utilizar una multiplicación para la resolución del problema. En la Figura 4 se presenta esta estrategia utilizada por el estudiante E34, al multiplicar el número de grupos de colores por un número que le permite aproximar al total en el problema Postes de Luz.

Figura 4
Estrategia Multiplicación

Suma-Resta Repetida (SRR)

Consiste en realizar sumas o restas repetidas hasta llegar al total. En la Figura 5 se presenta esta estrategia utilizada por el estudiante E33, al sumar tantas veces las 20 mesas hasta aproximarse a 103, en el problema Albergue.

Figura 5
Estrategia Suma-Resta Repetida

Conteo a Saltos (CS)

Consiste en contar a saltos teniendo en cuenta el número de elementos de un grupo o conjunto. En la Figura 6 se presenta esta estrategia utilizada por el estudiante E100 en el problema Albergue.

Figura 6
Estrategia Conteo a Saltos

Regla de tres (RT)

Consiste en relacionar los datos de manera multiplicativa igualando los productos cruzados. En la Figura 7 se presenta esta estrategia utilizada por el estudiante E82 en el problema Postes de Luz.

Figura 7
Estrategia Regla de tres

Uso de todos los datos (UTD)

Consiste en utilizar todos los datos del enunciado en diversas operaciones y dar una respuesta sin sentido. En la Figura 8 se presenta esta estrategia utilizada por el estudiante E52 en el problema Albergue.

Figura 8
Estrategia Uso de todos los datos.

Combinación de estrategias (CE)

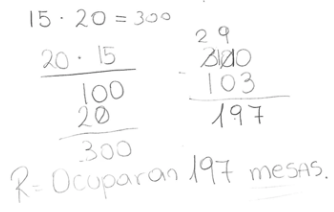
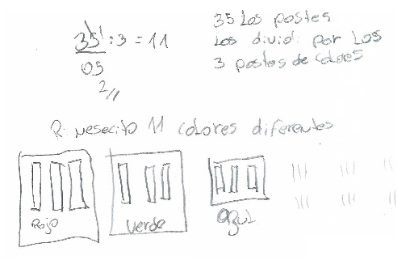
Consiste en utilizar dos estrategias; en particular, en este estudio, se identificaron casos donde se realiza un dibujo como apoyo (modelización-agrupamiento) y, además, se aplica un algoritmo (multiplicación o división). En la Figura 9 se presenta esta estrategia utilizada por el estudiante E20 en el problema Postes de Luz.

Figura 9
Combinación de estrategias

A continuación, se presentan los resultados, obtenidos a partir del análisis de los datos, en dos dimensiones: 1) éxito en la resolución del problema, y 2) estrategia utilizada en el mismo.

5.1. Éxito en la resolución del problema

La Tabla 1 muestra el porcentaje de éxito en la resolución de los tres problemas por los estudiantes de séptimo básico que participaron en el estudio.

Tabla 1
Frecuencia de éxito en la resolución de los problemas de división-medida por los estudiantes

Fuente: Elaboración propia

De manera general, los estudiantes tuvieron dificultades para resolver los problemas, especialmente en Pasteles y Albergue. El problema Postes de luz tuvo el mejor éxito de resolución (46/100), sin embargo, el porcentaje de éxito no superó el 50%, lo que evidencia las dificultades en la resolución de problemas de estructura multiplicativa.

Respecto a los estudiantes que respondieron de manera regular los problemas Postes de luz (30/100) y Albergue (19/100), no lograron identificar que se debía considerar el resto para dar respuesta a la pregunta planteada. Algunos de ellos se limitaron a indicar que la respuesta era el cociente de la división, o si realizaban un procedimiento alternativo al algoritmo, señalaban el resto (lo que les sobra) pero no lo consideraban para su respuesta, por ejemplo, el estudiante E21 en el problema Postes de luz señala “Son 11 colores diferentes, 2 colores sobran”. Otros, expresaron la respuesta en números decimales sin considerar el contexto del problema, es decir, se trata de una cantidad discreta y no continua; por ejemplo, el estudiante E10 en el problema Albergue responde: “Ocupa 5,15 mesas”. En el problema Pasteles, de los estudiantes que respondieron de manera regular (27/100), no lograron expresar lo que le sobra en fracción, por ejemplo, el estudiante E34, quien responde: “Puedo dar a 6 niños y me sobran dos trozos”.

Por otra parte, se resalta que el porcentaje de respuestas incorrectas más alto es el referente al problema Pasteles (29/100), esto debido a que prototípicamente los estudiantes tienden a usar una representación icónica asociada a círculos, en donde encuentran dificultades para dividirlo en quintos; y los que dividieron los pasteles en quintos, sólo representaron tres quintos de cada pastel sin tomar en cuenta que podían seguir formando grupos de tres hasta que sobren dos trozos de total. Esto pudo ocurrir, porque si bien la representación icónica apoyada en el círculo es una de las usan los profesores para introducir la noción de división, esta no es utilizada para resolver problemas de este tipo. En la Figura 10 se presenta la respuesta incorrecta del estudiante E89 al problema Pasteles.

Figura 10
Respuesta incorrecta de E89
en el problema Pasteles

Con respeto al problema Albergue y a los estudiantes que dieron una respuesta incorrecta, la mayoría utilizó el dato superfluo (innecesario) en su resolución, por ejemplo, el estudiante E52 (ver Figura 11); los demás, realizaron operaciones con todos los datos del enunciado o realizaron operaciones sin sentido. Así mismo, este problema presentó más dificultad para los estudiantes, considerando la suma de los porcentajes de aquellos que no lograron resolverlo y los que dieron una respuesta incorrecta.

Figura 11
Respuesta incorrecta de E52
en el problema Albergue

Con relación al problema Postes de luz y a los estudiantes que contestaron de manera incorrecta, se identificaron aquellas respuestas en las que se interpreta el enunciado de manera errónea asumiendo que se debían formar sólo 3 grupos pintando 12 postes rojos, 12 verdes y 11 azules, por ejemplo, el estudiante E91 (ver Figura 12); o bien, aquellos que realizaron varias operaciones utilizando todos los datos del enunciado, por ejemplo, el estudiante E31 (ver Figura 13).

Figura 12
Respuesta incorrecta de E91
en el problema Postes de Luz

-----

Figura 13. Respuesta incorrecta de E31 en el problema Postes de Luz

5.2. Estrategias utilizadas en la resolución del problema

Respecto a las estrategias de resolución, como se mencionó anteriormente, se identificaron 8 utilizadas por los estudiantes de séptimo básico: División (D), Modelación-agrupamiento (MA), Multiplicación (M), Suma-resta repetida (SRR), Conteo a saltos (CS), Regla de tres (RT), Uso de todos los datos (UTD) y Combinación de estrategias (CE);cabe señalar que no todas se ponen de manifiesto en los tres problemas.

En el problema Postes de Luz (ver Tabla 2), la estrategia más utilizada fue División (D) de las 8 que se identificaron, aunque no tuvo mayor éxito en la resolución, pues menos de la mitad de los estudiantes que utilizaron esta estrategia lograron resolverlo de manera correcta. Sin embargo, las estrategias Modelación-agrupamiento (MA), Multiplicación (M) y Combinación de estrategias (CE), tuvieron mejor éxito de resolución con respecto a los que utilizaron el algoritmo de la División (D), pues más de la mitad de los que utilizaron estas estrategias lo hicieron de manera correcta.

Tabla 2
Frecuencia (y porcentaje) de las estrategias utilizadas
por los estudiantes en el problema Postes de Luz

Fuente: Elaboración propia

En el problema Albergue (ver Tabla 3), siete de las ocho estrategias se ponen de manifiesto en la resolución de este problema (no se utilizó Regla de tres, RT), siendo División (D) la más utilizada, al igual que en caso de Postes de Luz; sin embargo, el éxito en la resolución fue mejor, ya que la mitad lo realizó de manera correcta. Un hecho relevante en la resolución de este problema es que las estrategias con mayor éxito de resolución son Combinación de estrategias (CE) y conteo a saltos (CS), aunque no están entre las más utilizadas; es decir, de los estudiantes que utilizaron estas estrategias, la mayoría lo hizo de forma correcta.

Tabla 3
Frecuencia (y porcentaje) de las estrategias utilizadas
por los estudiantes en el problema Albergue

Fuente: Elaboración propia

En el problema Pasteles (ver Tabla 4) se utilizaron seis de las ocho estrategias (no se utilizó Conteo a saltos y Regla de tres). La estrategia más utilizada fue Modelación-agrupamiento (MA), esto pone en evidencia su utilización cuando se trata de un problema que involucra números fraccionarios; sin embargo, menos de la mitad de los que usaron esta estrategia lograron hacerlo de manera correcta. De los que realizaron el problema regular y utilizaron Modelación-agrupamiento (MA) como estrategia, no expresaron la respuesta a la segunda pregunta en términos de fracción, por ejemplo, el estudiante E36 responde “puedo dar a 6 niños y me sobran dos”. De los que realizaron el problema de manera incorrecta usando la misma estrategia (MA), representaron los pasteles graficando círculos, pero no lograron hacerlos de forma correcta, dividiendo las tortas en tercios en vez de quintos. Otros al representar los 4 pasteles, coloreaban 3/5 de cada pastel, sin considerar que de cada pastel sobraban 2/5 que se podrían reagrupar nuevamente y dar a más niños 3/5 de pastel. Por otra parte, aunque se ponen de manifiesto otras estrategias, como la División (D) por ejemplo, al igual que en los demás problemas, aplicar el algoritmo no garantizó el éxito en la resolución, ya que menos de la mitad resolvió el problema de manera correcta.

Tabla 4
Frecuencia (y porcentaje) de las estrategias utilizadas
por los estudiantes en el problema Pasteles

Fuente: Elaboración propia

En los tres problemas, Postes de Luz, Albergue y Pasteles, se puso de manifiesto la estrategia Uso de todos los datos (UTD) para tratar de responder las preguntas planteadas, en algunos casos realizando diversas operaciones sin lograr dar solución, o bien, dan respuestas incorrectas; por ejemplo, estudiante E95 en el problema Postes de Luz escribe “rojo, verde y azul, necesito tres colores”. 

En resumen, los resultados obtenidos tras el análisis del éxito de la respuesta y de las estrategias utilizadas nos muestran que los estudiantes tuvieron dificultades en la resolución de problemas de división-medida; en particular cuando se tenía que dividir un entero entre una fracción e interpretar el resto de la división. Por otra parte, el algoritmo de la división fue el procedimiento más empleado por los estudiantes cuando resolvían los problemas de división-medida utilizando números enteros, sin embargo, ante las dificultades que presenta la división de un entero entre una fracción, los métodos alternativos fueron los más utilizados por los estudiantes para resolver el problema Pasteles con éxito.

Otro aspecto a destacar en los resultados obtenidos es el hecho de que los estudiantes de séptimo básico aunque utilizan la división como estrategia de resolución de estos problemas, no es la única que se pone de manifiesto ni la que tiene mejor éxito de resolución. Las estrategias alternativas (modelación-agrupamiento, conteo a saltos, suma-resta repetida) se ponen de manifiesto y con mejor éxito de resolución en más de la mitad de los estudiantes que utilizaban esas estrategias.

Este estudio examina las estrategias utilizadas por estudiantes chilenos de séptimo básico (12-14 años) cuando resuelven problemas de estructura multiplicativa, específicamente de división-medida. Los resultados nos han permitido evidenciar las estrategias utilizadas por los estudiantes cuando resuelven este tipo de problemas y las características del uso de esas estrategias en relación al nivel de éxito de resolución.

Menos del 50% de los estudiantes resolvió de manera correcta los problemas de estructura multiplicativa de división-medida, Postes de Luz y Albergue, donde intervienen números naturales, y mayor dificultad en el problema Pasteles (39%) donde está implicada una división de un entero entre una fracción. Esto nos indica las dificultades que tuvieron los estudiantes a la hora de resolver los problemas de división-medida donde debían interpretar el resto añadiendo una unidad al cociente o donde debían hacer una división de un entero entre una fracción e interpretar también el resto. Nuestros resultados muestran una tendencia entre los estudiantes a excluir el conocimiento del mundo real para interpretar el resto de la división entre dos enteros y dar una respuesta correcta al problema de división-medida al igual que en el estudio de Verschaffel et al. (1997) y Lago et al. (2008). Este resultado se hace más evidente en los problemas en los que está implicada la división de un entero entre una fracción.

La estrategia más empleada en la resolución de los problemas Postes de Luz y Albergue fue División y en menor medida otros procedimientos alternativos como Suma-resta repetida o Conteo a saltos. Por otro lado, en el caso de Pasteles la más utilizada es Modelización-Agrupamiento seguida del de la División. En los resultados se muestra una variedad de estrategias utilizadas por los estudiantes, inclusive la Combinación de estrategias, desde Uso de todos los datos hasta Regla de tres en menor grado. Este resultado difiere de lo evidenciado en Ivars y Fernández (2016) donde los estudiantes en sus primeros años de estudio disponen de un repertorio amplio de estrategias que les permiten solucionar con cierta solvencia problemas de estructura multiplicativa, pero a medida que avanzan los cursos (en nuestro caso séptimo básico), van abandonando estas estrategias y se utilizan, casi exclusivamente, la aplicación del algoritmo de la División de manera mecánica. Así mismo, Silver, Shapiro y Deutsch (1993) manifiestan que, en estudios previos con estudiantes de Educación Primaria, la tendencia de aquellos que conocen el algoritmo de la división es utilizarlo para resolver los problemas de división-medida. Sin embargo, en nuestro estudio esta tendencia no es tan evidente.

En el problema Pasteles, los estudiantes tuvieron mayor éxito con respecto a la respuesta correcta cuando aplicaron la estrategia Modelización-agrupamiento (basada en una representación icónica); esto por las dificultades que presentaron en la realización de una división de un entero entre una fracción, mismas que son debidas a no poder de identificar cuál es la unidad de medida (Izsák, Jacobson, De Araujo y Orrill, 2012; Rosli, González y Capraro, 2011).

Otro aspecto a destacar es el hecho de que la mayoría de los estudiantes tuvo mayor dificultad en el problema Albergue por el uso del dato superfluo que había en el problema; además, influye el hecho de asumir que el resto de una operación no debe considerarse en el resultado final. En la resolución del problema Pasteles con la división de un entero entre una fracción, los estudiantes no fueron capaces de expresar el resultado en términos matemáticos, por ejemplo, no escribieron en fracción la respuesta a la segunda pregunta del problema Pasteles diciendo “2 trozos”. Esto nos sugiere analizar con profundidad, en un futuro estudio, los errores cometidos por los estudiantes.

Si tomamos en cuenta que la resolución de problemas es considerada una competencia fundamental del Ciclo Básico en Chile, debemos brindar oportunidades a los estudiantes para desarrollar esta competencia, a través de estrategias de resolución que les permita la comprensión de los mismos y puedan ser usadas en situaciones diversas. Esto implica que tanto los profesores de Educación Básica como los estudiantes para profesores, deben tener en el proceso de formación herramientas que le permitan desarrollar en la resolución de problemas matemáticos, identificar diferentes estrategias usadas por sus alumnos, interpretar la comprensión matemática que ponen de manifiesto y tomar decisiones relativas a la enseñanza teniendo en cuenta dicha comprensión (Jacobs, Lamb y Philipp, 2010).

Consideramos que esta información puede ser útil para una propuesta de formación de profesores de Educación Básica, en cuanto a la resolución de problemas de este estilo.

Aunque reconocemos que nuestra muestra es pequeña para generalizar los resultados, pudimos identificar aspectos que necesitan mayor investigación. Este trabajo nos deja la línea futura de analizar la reflexión que desarrollan los profesores a las respuestas que dan los estudiantes a este tipo de problemas.

Callejo, M.L. y Vila, A. (2009). Approach to mathematical problem solving and students’ belief systems: two case studies. Educational Studies in Mathematics, 72(1), 11-126.

Downton, A. (2009). A study of comparative performance on partitive and quotitive division in solving division word problems. En M. Tzekaki, M. Kaldrimidou y H. Sakonidis (Eds.), Proceedings of the International Group for the Psychology of Mathematics Education, Vol. 2. (pp. 465-472). Thessaloniki, Greece: PME.

Espinoza, L., Barbé, J. y Gálvez, G. (2011). Limitaciones en el desarrollo de la actividad matemática en la escuela básica: el caso de la aritmética escolar. Estudios Pedagógicos, 37(1), 105-125.

García, M. y Suárez, A. (2011). Procedimientos de resolución de problemas multiplicativos de isomorfismo de medidas. En P. Perry (Ed.), Memorias del XX Encuentro de Geometría y sus Aplicaciones (pp. 213-220). Bogotá, Colombia: Universidad Pedagógica Nacional.

Gómez, B. y Contreras, M. (2009). Sobre problemas multiplicativos relacionados con la división de fracciones. PNA. Revista de Investigación en Didáctica de la Matemática, 3(4), 169-183.

Ivars P. y Fernández C., (2016). Problemas de estructura multiplicativa: Evolución de niveles de éxito estrategias en estudiantes de 6 a 12 años. Educación Matemática, 28(1), 12-38.

Izsák, A., Jacobson, E., De Araujo, Z. y Orrill, C. H. (2012). Measuring mathematical knowledge for teaching fractions with drawn quantities. Journal for Research in Mathematics Education, 43(4), 391-427.

Jacobs, V., Lamb, L. y Philipp, R. (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education, 41(2), 169-202.

Lago, M. O., Rodríguez, P., Enesco, I. E., Jiménez, L., & Dopico, C. (2008). Me sobran cuatro y no sé qué hacer con ellos. Un estudio sobre los problemas de división con resto en alumnos de 1º de ESO. Anales de Psicología/Annals of Psychology, 24(2), 201-212.

Li, Y. y Silver, E.A. (2000). Can younger students succeed where older students fail? An examination of third graders’ solutions of a division-with-remainder (DWR) problem. Journal of Mathematical Behavior, 19(2), 233-246.

Lima, R. R. y Carvalho, M. (2013). Algumas estratégias de resolução de problemas de divisão. Boletim GEPEM, 62, 87–100.

Llinares, S. y Sánchez, V. (1998). Aprender a enseñar, modos de representación y número racional. En L. Rico y M. Sierra (Eds.), Primer Simposio de la Sociedad Española de Investigación en Educación Matemática (pp. 15–26). Granada, España: SEIEM.

MINEDUC (2013). Matemática Educación Básica. Bases curriculares en Educación Básica. Santiago de Chile: Autor.

Rosli, R., González, E.G. y Capraro, M.M. (2011). A case study of three preservice teachers on the units and unitizing of fractions. En L.R. Wiest y T. Lamberg (Eds.), Proceedings of the 33rd Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 1682-1689). Reno, NV: University of Nevada, Reno.

Silver, E.A., Shapiro, L.J. y Deutsch, A. (1993). Sense making and the solution of division pro-blems involving remainders: An examination of middle school students’ solution processes and their interpretation of solutions. Journal for Research in Mathematics Education, 24(2), 117-135.

Vergnaud, G. (1983). Multiplicative structures. En R. Lesh y M. Landau (Eds.). Acquisition of math concepts and processes (pp. 127–174). London: Academic Press.

Vergnaud, G. (1997). El niño, la matemática y la realidad. México: Trillas.

Verschaffel, L. y De Corte, E. (1997). Word problems: A vehicle for promoting authentic mathematical understanding and problem solving in the primary school? En: T. Nunes y P. Bryant (Eds.). Learning and Teaching Mathematics. An International Perspective (pp. 69-98). Hove: Psychology Press.

1. Doctora en Investigación Educativa, Universidad de Alicante, España. Académica del Departamento de Ciencias Exactas, Universidad de Los Lagos, Osorno, Chile. Correo electrónico: maximina.marquez@ulagos.cl

2. Doctora en Ciencias, Especialidad en Matemática Educativa, CINVESTAV-IPN. Académica del Departamento de Ciencias Exactas. Universidad de Los Lagos, Osorno, Chile. Correo electrónico: elizabeth.hernandez@ulagos.cl

3. Doctor en Ciencias, Especialidad en Matemática Educativa, CINVESTAV-IPN. Académico del Departamento de Ciencias Exactas. Universidad de Los Lagos, Osorno, Chile. Correo electrónico: jaime.garcia@ulagos.cl