ISSN 0798 1015

Vol. 39 (# 20) Year 2018. Page 16

The choice of an optimal methodology for the retraining organization of psychologists based on the use of mathematical methods

La elección de la metodología óptima para la organización de la recapacitacion de expertos psicólogos en base al uso de métodos matemáticos

Valery B. VILKOV 1; Olga I. SHCHERBAKOVA 2; Andrey K. CHERNYKH 3; Vladislav Р. АNDREEV 4; Tatyana L. KHUDYAKOVA 5; Svetlana N. KAZAKOVA 6

Received: 02/03/2018 • Approved: 15/04/2018

Contents

1. Introduction

2. Methodological Framework

3. Results

4. Discussion and Conclusion

5. Recommendations

Bibliographic references

1. Introduction

Mathematical methods are applied practically in all the spheres of human activity. Psychological sciences also tend to use mathematics as evidence-based methods. Since the 1970s, the theory of fuzzy sets has been playing an increasingly important role in the use of mathematics, which is widely employed in solving technical problems, decision-making tasks in management, the probability theory is used in conflict studies and economics. The first pioneers in creating a realistic theory of making rational decisions in conflict situations were J. von Neumann & O. Morgenstern (1970), N. Howard (1971), and many others (Mamdani & Assilian, 1975; Piegat, 2001; Sibgatova et al., 2016; Efimova et al., 2017; Enyashina et al., 2017; Ganieva et al., 2015; Kalinina et al., 2017; Masalimova & Chibakov, 2016; Mitin et al., 2017a; Mitin et al., 2017b; Salakhova et al., 2017a; Salakhova et al., 2017b; Salakhova et al., 2017c; Klepach & Borodovitsyna, 2017; Galushkin, 2017a,b).

The latter circumstance also predetermined the use of the specified mathematical system by the authors in order to determine the maximum level of reliability of the fulfillment by each of the retrained (additional education, advanced training) candidates of their official duties in a position for which it is advisable to appoint one.

The fact that the problem is solved within the assumption that the information about the  relevance of a candidate  after training to competencies of a candidate’s respective specialty and the level of his relevance  to a job has an ambiguous, fuzzy character gives this article  topicality  and novelty.

We will present the required information for further reasoning from the graph theory (Berg, 1962; Chernykh & Vilkov, 2016; Ore, 1968; Masalimova et al., 2014; Mitin, 2016).

The subject of the graph theory is the study of relationships between knots (within the framework of the article – the retraining elements of candidates). The knots are called vertices, and the links between them are edges.

We need to note that in order to reduce the volume of this article, we will sometimes not replace these two terms with terms from the candidates’ retraining process that is analyzed in the article.

A graph G = (V, E) is the pair of sets including the set of vertices V and the set of edges E. The examples of graphs are: the plans of complexes of measures; hierarchical structures, systems of relationships between people and organizations; structured programs of education and retraining, etc.

Let u and v be vertices of the graph G. The edge joining these vertices will be denoted by (u, v), say that the vertices u and v are incidents to the edge (u, v), and the edge (u, v) is incident to the vertices u and v. The vertices u and v are called finite for the edge (u, v).

A weighted edge is an edge that corresponds to a certain number. For example, if the edge (u, v) means that the candidate u was retrained for the program v, then the weight of this edge can be the quality assessment of the material learnt or the reliability of the candidate’s successful  mastering the retraining program.

A weighted graph is a graph whose entire edges are weighted. If (u, v) = (v, u), then the edge (u, v) is called non-oriented. A continuous sequence of non-oriented edges is called a chain.

A sub-graph of the graph G = (V, E) is the graph F = (W, D), all of whose vertices and edges are respectively the vertices and edges of the graph G. A three-vertex ensemble is the chain consisting of two edges and containing three distinct vertices.

By a three-vertex combination P in the graph G = (V, E) we mean a set of three-vertex ensembles of G such that any two distinct ensembles of P are not adjacent; i.e. they have no common vertices. If all the vertices of a graph are vertices of edges of the three-vertex combination under consideration, then this combination is called complete. The graph G = (V, E) is called a tripartite one, by analogy with a bipartite one, if the set of its vertices splits into three disjoint parts V1, V2, V3, if so  , then either  or  either  and  (Figure 1).

Figure 1
The tripartite graph

Within the framework of the proposed methodology, we will give some concepts of the theory of fuzzy sets and fuzzy logic (Kofman, 1982; Terano, Asai & Sugeno, 1993; Shtovba, 2001).

The concept of a fuzzy set is an attempt of mathematical formalization of fuzzy information for constructing mathematical models. It is assumed that the elements composing a given set, possessing some common property, can possess this property in different degrees and, consequently, belong to a given set with different degrees. Speaking of the fact that an element belongs to a given set, it is necessary to indicate to what extent it satisfies the properties of this set. The following concepts and results of the theory of fuzzy sets and fuzzy logic are given, for example, in the works (Zadeh, 1976; Leonenkov, 2005; Orlovsky, 1981; Chernykh et al., 2015; Vilkov & Chernykh, 2016; Yakhyaeva, 2006; Zadeh, 1965).

3. Results

Let us return to the problem, the verbal statement of which is given at the beginning of the article. Let us give it a clear statement in terms of the graph theory.

Figure 2
The graph of the fuzzy number membership function

We will get back to consideration of the task of choosing the optimal plan for the implementation of the psychologists’ retraining program and their subsequent appointment to vacant positions (hereinafter, the appointment task).

In the terms formulated above, this is the task of constructing a complete three-peak combination.

To solve this task, we will use the algorithm for solving the transport task with intermediate points, for example, from H.M. Wagner's (1972) monograph.

Let us formulate the statement of the transport problem with intermediate points in terms of the appointment task.

Step 3. Let us find the weight (let it be equal to m) of the resulting three-peak combination of the graph and remove all edges from the graph under consideration whose weight does not exceed m, for which we will assume that the weight of such edges is equal to a large number, for example, 100, that making it unacceptable to use such edges for the retraining of candidates in retraining programs corresponding to these edges or appointing candidates who have completed retraining programs to fill vacant positions that correspond to these edges.

Step 4. Considering the resulting graph as the initial information for solving the appointment problem, we go on to Step 1.

Remark 3. The iteration of the algorithm (steps 1-4) is performed until we obtain a graph that does not have the desired three-peak combination. The combination obtained in the previous step is the one we are looking for.

Step 5. Stop.

Let us illustrate the theoretical basis of the proposed algorithm on an informative example.

Four candidates must undergo retraining in one of the four retraining programs and then fill four vacant positions.

Table 1
Initial data for determining the order of candidates’ retraining

The initial data of the appointment problem (transport problem) are given in Table 3.

Remark 4. Due to the fact that for the solution of the appointment problem we use the algorithm for solving the transport problem, in which the objective function is minimized, the differences between the maximum (unit) and the resulting reliability values are used as the characteristics of the edges.

Table 2
Initial data for determining the procedure to fill vacant positions

Table 3
Initial data for the appointment problem (transport problem)

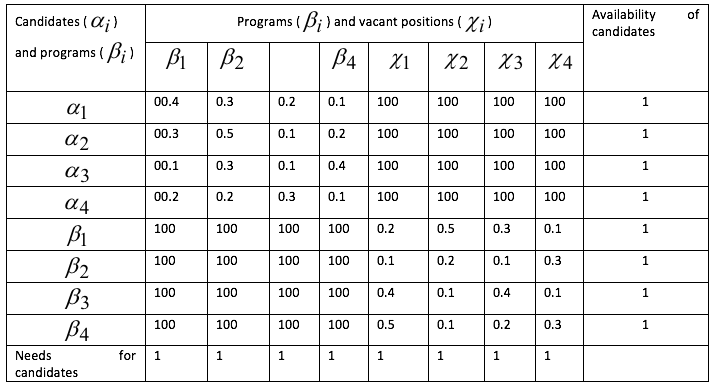
As a result of solving the appointment problem using the method of solving the transport problem, we obtain the optimal solution (plan) in the form of a full three-peak combination of maximum weight (the reliability of the three-peak ensembles is shown in brackets):

We would like to note that the reliability of the three-peak ensemble is equal to the minimum of the reliability of its edges, the reliability of the complete three-peak combination, in accordance with formula (2) is equal to the minimum of the reliability of the three-peak ensembles of its components, and, consequently, is 0.8.

In accordance with the instructions of step 3, we prohibit the use of edges by reliability of 0.8 and less - (in Table 3 - 0.2 and more) and we carry out the decision of the appointment problem with the received data. For the example considered in this article, this problem does not have possible solutions (plans) and, therefore, the optimal solution (plan) of the problem is the solution (3) obtained at the previous iteration.

Let us give a verbal formulation of the optimal solution (3) of the appointment problem: the first candidate was trained in the fourth program and took the third position; the second candidate was trained in the third program and took the second position; the third candidate was trained according to the first program and took the fourth position; the fourth candidate was trained in the second program and took the first position.

Since the 80-s of the last century, the so-called "boom of fuzziness" has begun, associated with the very intensive application in the various fields of human activity of the methods of the theory of fuzzy sets, created in 1965 by Professor L.A. Zadeh (1965).

This article is a continuation of publications in this direction, it is devoted to the application of this theory to solve problems of considerable interest for specialists involved in the organization of the educational process.

New results comprise the formulation of the problem considered in the article using fuzzy numbers and tripartite graphs; the method of solving it with the use of the algorithm for solving the transport problem of linear programming with intermediate points; the algorithm for constructing a full three-peak combination of maximum weight, in the sense considered above, on a tripartite graph.

Thus the methodology has been proposed that provides  the optimal procedure for the retraining organization of psychologists that simultaneously takes into account the difference in their training programs and the procedure for their subsequent appointment to vacant positions which with the software application can be used to solve a wide range of tasks in various fields, not only education, but also management, national economy.

5. Recommendations

The proposed methodology for organizing psychologists’ retraining is universal, because it can be used not only by human resource departments, psychologists, but also by other personnel services to select the most competent employees. It can be of use to staff members of the Ministry of Education and Science who solve the problems of the required competence structure of the graduates of educational institutions. In addition, it can be useful for researchers in various fields of the national economy that carry out development work in solving similar problems.

Berg, C.K. (1962). The theory of graphs and its applications. Moscow: IL.

Chernykh, A.K., Kozlova, I.V. & Vilkov, V.B. (2015). Questions of forecasting of material support with use of fuzzy mathematical models. Problems of risk management in the technosphere, 4(36), 107-117.

Chernykh, A.K. & Vilkov, V.B. (2016). Management of the safety of transportation in the organization of material support of forces and facilities of the Ministry of Emergency Situations of Russia in emergency situations. Fire and explosion safety, 25(9), 52-59.

Efimova, O.I., Oshchepkov, A.A., Chirkovskaya, E.G., Klepach, Y.V. & Gridyaeva, L. N. (2017). The Experience of Studying Specific Features of Social Attitudes and Value Orientations among Normative and Deviant Teenagers. Eurasian Journal of Analytical Chemistry, 7(12), 1549-1553. 

Enyashina, N.G., Gridnevа, S.V., Khudyakova, T.L., Gridyaeva, L.N., Pozharskay, E.L. & Deberdeeva, N.A. (2017). Development of Higher Education Students’ Creative Abilities in Learning and Research. Eurasian Journal of Analytical Chemistry, 12, 753–763.

Galushkin, A.A. (2017a). Operational management of enterprise structures in the sphere of education and science: Problems and methods for their solution. European Research Studies Journal, 20(4), 412-420.

Galushkin, A.A. (2017b). Organizations of the sphere of education and science methods of competitiveness improvement. European Research Studies Journal, 20(4B), 421-431.

Ganieva, Y.N., Sayfutdinova, G.B., Yunusova, A.B., Schepkina, N.K., Scheka, N.Y., Gutman, E.V. & Salakhova, V.B., (2015). Structure and content of higher professional school lecturer education competence. Review of European Studies, 7(4), 32-38.

Howard, N. (1971). Paradoxes of Rationality: Theory of Metagames and Political Behavior. Cambridge: The MIT Press.

Kalinina, N.V., Salakhova, V.B., Artamonova, E.G, Efimova O.I., Kalinin, I.V. (2017). Psychological Prevention Mechanisms of Minors’ Deviant Behavior. Eurasian Journal of Analytical Chemistry, 12, 663-672

Klepach, Yu.V. & Borodovitsyna, T.O. (2017). Features of the i-concept of teachers. Izvestia Voronezh State Pedagogical University, 275(2), 86-89.

Kofman, A. (1982). Introduction to the theory of fuzzy sets. Moscow: Radio and communication.

Leonenkov, A.V. (2005). Fuzzy modeling in MATLAB and fuzzyTECH. St. Petersburg: BHV-Petersburg.

Mamdani, E.H. & Assilian, S. (1975). An Experiment in Linguistic Synthesis with Fuzzy Logic Controller. J. Man-Machine Studies, 7(1), 1-13.

Masalimova, A.R., Schepkina, N.K., Leifa, A.V., Shaidullina, A.R. & Burdukovskaya, E.A. (2014). Mentoring perfection in modern enterprises conditions: practical recommendations. American Journal of Applied Sciences, 11(7), 1152-1156.

Masalimova, A.R. & Chibakov, A.S. (2016). Experimental analytical model of conditions and quality control of vocational training of workers and specialists. Mathematics Education, 11(6), 1796-1808.

Mitin, S.N. (2016). Psychotherapeutic approach in the management of the development of educational systems. Simbirsk Scientific Bulletin, 4(26), 31-39.

Mitin, S.N., Belinskaya, D.B., Vasyakin, B.S., Kamneva, E.V. & Lipatova, N.V. (2017a). A socionomic approach in studying key types of the peronality’s viability. Modern Journal of Language Teaching Methods, 5, 18-28.

Mitin, S.N., Shukshina, L.V., Bazhdanova, Y.V., Koretskaya, I.A. & Vasyakin, B.S. (2017b). Value and meaning attitudes as a factor of forming tolerant ethnic consciousness in the multicultural milieu of a higher education institution. Eurasian Journal of Analytical Chemistry, 12(7), 1193-1200.

Neumann, J., Morgenstern, O. (1970). Game theory and economic behavior. Moscow: Nauka.

Ore, O. (1968). Graph theory. Moscow: Science.

Orlovsky, S.A. (1981). Decision problems with fuzzy source information. Moscow: Science. Main edition of physical and mathematical literature.

Piegat, A. (2001). Fuzzy Modeling and Control. New York: Springer.

Salakhova, V.B., Kalinina, N.V., Belinskaya, D.B., Aygumova, Z.I. & Tkhugo, M.M. (2017a). Education as a factor of raising the adaptation potential in a delinquent personality. Man In India, 97(3), 1-13.

Salakhova, V.B., Tashcheva, A.I., Gridnevа, S.V., Zhmurin, I.E. & Mikhaylovsky, M.N. (2017b). Experimental study of social and psychological correction of the teenage peronality’s values and motivation sphere who is prone to deviant behavior. Modern Journal of Language Teaching Methods, 7(4), 12-20.

Salakhova, V.B., Tkhugo, M.M., Shalamova, L.F., Polevaya, M.V. & Pozharskaya, E.L. (2017c). Intergration resources of the personality in the context of human existence modes. Man in India, 97(9), 121-130.

Shtovba, S.D. (2001). Introduction to the theory of fuzzy sets and fuzzy logic. Vinnitsa: UNIVERSUM-Vinnitsa.

Sibgatova, K.I., Ilchinskaya, E.P., Bastrikova, E.M., Kuramshina, L.L., Makarov, A.L., Chernova, N. Y., Khairullina, E.R. & Murugova, V.V. (2016). The traditional and innovative technologies of vocational guidance work with pupils and students. International Review of Management and Marketing, 6(2s), 97-103.

Terano, T., Asai, K. & Sugeno, M. (1993). Applied inaccurate systems. Moscow: The World.

Vilkov, V.B. & Chernykh, A.K. (2016). Theory and practice of optimization of managerial decisions in conditions of emergency situations in transport. St. Petersburg: St. Petersburg State University of Emergency Situations Ministry of Russia.

Wagner, H.M. (1972). Basics of Operations Research. Moscow: The World.

Yakhyaeva, G.E. (2006). Fuzzy sets and neural networks. Moscow: Binom.

Zadeh, L.A. (1976). The concept of a linguistic variable and its application to the adoption of approximate solutions. Moscow: The World.

Zadeh, L.A. (1965). Fuzzy sets.  Information and Control, 8(3), 338-353.

1. Department of General Scientific and Technical Disciplines. Military Academy of Material and Technical Supply name of A.V. Khruleva, St. Petersburg, Russia. Contact e-mail: amirusha@rambler.ru

2. Department of Psychology Plekhanov Russian University of Economics, Moscow, Russia

3. Department of Mathematics and Informatics Sankt Petersburg Military Institute of the National Forces Guard of the Russian Federation, St. Petersburg, Russia

4. Department of Mathematics and Informatics Sankt Petersburg University of the Ministry of Internal Affairs of Russia, St. Petersburg, Russia

5. Department of Practical Psychology, Voronezh State Pedagogical University, Voronezh, Russia

6.Department of Management of Nursing Activities and Social Work, The Sechenov First Moscow State Medical University, Moscow, Russia