ISSN 0798 1015

Vol. 38 (Nº 48) Year 2017. Page 36

Increasing geometric homogeneity of dispersed particles of plastic materials produced by vibration assisted micro-cutting

Aumento de la homogeneidad geométrica de las partículas dispersadas de materiales plásticos producidos por el micro-corte asistido por vibración

Yuriy SERGEEV 1; Sergey SERGEEV 2; Alexander D’YAKONOV 3

Received: 30/09/2017 • Approved: 05/10/2017

Content

1. Introduction

2. Methods

3. Data, Analysis, and Results

4. Discussion

5. Conclusion

Acknowledge

References

1. Introduction

A high level of requirements for modern high-tech products has necessitated the production of a wide range of composite materials with specified physical and mechanical properties. At the same time, we are able not only to control the performance properties of composites by varying the composition, ratio, orientation of filler particles different in shape and size (Chumanov et al., 2010; 2012), but also to create new ones (Chumanov et al., 2015; 2017).

The prospects for materials science development are conditioned by the demand for new materials with unique properties and efficient manufacturing technology, as the requirements for their properties are constantly changing. Powders, fibers, granules and light metal pastes are widely used in various fields of engineering: metallurgy (Gordeev, Sergeev & Chumanov, 2010), chemistry (Sergeev & Gordeev, 2009), medicine (Salernitano & Migliaresi, 2003), energy (Sandalov & Sergeev, 2012), building and construction (Lakirev et al., 2003), nuclear (Sergeev, 2011), space, military technology (Balaykin, Smelov & Chempinskiy, 2012) and other industries, as they have new (in comparison with compact materials) properties, based on specific surface properties of dispersed materials (Sergeev & Gordeev, 2010) (various metal and non-metal composite materials). They are produced by reducing metal oxides or metal salts to metal, by electrolytic deposition, by plasma spraying, by electrospark dispersion, and by mechanical methods: cutting, grinding, abrasion, and etc. The technological features of these processes determine their scope of implementation and economic feasibility. Such a variety is based on different requirements to physical, chemical, mechanical and performance properties of dispersed materials. However, all these processes are being improved to increase productivity while maintaining the physicochemical properties of materials and, mainly, producing particles of desired shape and size in stable dispersion. Therefore, all manufacturers producing components for composite materials face an acute problem of providing the required particle geometry and particle uniformity that largely determine the performance properties of a product.

Physicochemical and mechanical dispersion methods used in industry have the following drawbacks. Physicochemical dispersion of metals and plastics involves physicochemical feedstock transformations. As a result, produced material is chemically or physically different in comparison with the feedstock. Mechanical granulating methods transform the feedstock into granular-like chips, fibers and even into powder without a noticeable change in its chemical composition. There are such widely used methods as granulating through cutting (shredding machines), abrasion and grinding (ball, vortex and hammer grinders), but the last two methods are advisable to use only for treating brittle materials. The process of grinding viscous and plastic materials (zinc, aluminum, copper, great part of thermoplastics) is difficult, since they are mainly flattened, not destructed. On the contrary, the process of granulating through cutting allows treating these viscous materials. Treated metal must be granulated into chips and have, at the same time, stable size and shape, since non-uniform particle-size distribution (PSD) of granulated metal entails defects (chipping, swelling, excessive or uneven porosity) and, as a consequence, deterioration of physical-mechanical properties of the final product. At the same time, the process of granulating through cutting does not allow making a desired shape and providing a desired PSD of dispersed material while the existing granulating methods are physically highly demanding. Therefore, high cost of manufacturing powder, especially metal powder, holds the producers from wider distribution of products made of composite materials. There is a need to produce granule like chips while treating wastes, for example – metallurgical slags (Sergeev, Sergeev & Karpov, 2016) and plastics (Sergeev & Gordeev, 2010), for the second time. Meanwhile, up to 50% of secondary raw materials can be added to the feedstock while manufacturing products based on thermoplastics, and up to 20% –while sintering products made of thermoset material if the last meets the specified PSD. In treating thermoplastics, non-uniform size of the cut-off material and its significant deviations from a desired shape lead to a number of defects in products obtained of it (non-melts, burnings, cracks, etc.). In terms of injection molding machines, there are always requirements for the size and shape of used thermoplastic granules, while the allowed deviation of the final particle size from the required should not be more than 15%. In sintering products made of thermosetting plastics, it is recommended to add secondary powder materials, which degree of dispersion should be 0.02 ... 0.05 mm. The latter cannot be obtained with existing cutting mills.

Summarizing the above, we should note that the considered methods have certain requirements for the granulate particle size and particle shape. In plant operating conditions, granulate particles with specified sizes and shapes are produced irregularly while grinding raw materials and waste. High dimensional heterogeneity and existing deviations from the specified shape of the cut-off segments lead to a number of defects in products obtained of it. This problem is particularly urgent when waste is being dispersed by milling, since such method is widely used because it is simple to implement and works fine with various engineering materials combining elastic and viscous properties. These difficulties are explained by insufficient knowledge of how the chips separate while the segments are being cut. There are also no substantiated recommendations how to control the process of shaping final particles. In this regard, there is an urgent task to improve the process of forming a cut-off segment while dispersing materials.

2. Methods

Physical phenomena occurring during mechanical dispersion are peculiar, as it has not been possible (until now) to build a unified physical theory of such processes that would explain the whole set of empirically well-known facts and predict new effects and phenomena. The problems in mechanics associated with the penetration and motion of solids in the continuous (solid) media are the least studied part of mechanics. Moreover, issues related to rotating instruments, namely their rotation motion in solid media, are not considered as problems of mechanics. Thus, no one seriously studies them be means of mathematical modeling. Since the issues of modeling the movement of multiple-cutting-edge tools in a metal workpiece and the movement of a grinding tool on the surface of formation are attached to the applied branches of science, the level of knowledge of such processes is immeasurably behind the level of knowledge of mechanical motion in other media. This situation is further aggravated by the fact that modern production technologies are based more on the experience of engineering practice, rather than on scientific research. In this regard, increasing efficiency of a particular development is largely based on the knowledge of the physical nature of related processes. Numerous attempts to attract professional mathematicians to the mathematical modeling of specific engineering problems, in most cases, do not drive to success, since successful solution of the applied problem requires a deep understanding of its essence.

3. Data, Analysis, and Results

Our analysis of performed work shows that when it comes to material dispersion as the increment of new surfaces, various researchers agree only in that particle dispersion is dependent on such factors as non-homogeneity and anisotropy of media (Sumelka, Zaera & Fernández-Sáez, 2016; Ouelaa et al., 2017; Gordienko, Mustyatsa & Kovaleva, 2016). The remaining issues are highly debatable; various hypotheses and scattered empirical facts are in contradiction.

Despite a large number of research papers, they are focused mainly on studying and improving energy-consuming and costly ways to produce powders and fibers, such as reducing metal oxides or metal salts to metal, electrolytic deposition, plasma spraying and electrospark dispersion (Kalpakjian & Schmid, 2014; Şahin & Yalcinkaya, 2016; Hayes, 2014). There are attempts to study and improve mechanical methods of dispersion (Hamran & Rashid, 2017; Webster & Eren, 2014; Parveen, Rana & Fangueiro, 2013). Their results are provided mainly to increase the process productivity while maintaining the physicochemical properties of materials. As a result, used methods lag behind, and the equipment is morally obsolete.

Therefore, research on material fracture mechanics, associated with the process of developing the fundamentals of chip geometry control and its surface uniformity control while forming the rotating multiple-cutting-edge tools through forcibly changing the amplitude-phase-frequency characteristics of their transverse oscillations (Lakirev et al., 2003; Sergeev et al., 2009), will become a scientific basis for the improvement of modern vibration technologies, used in the course of solid dispersion in condensed media.

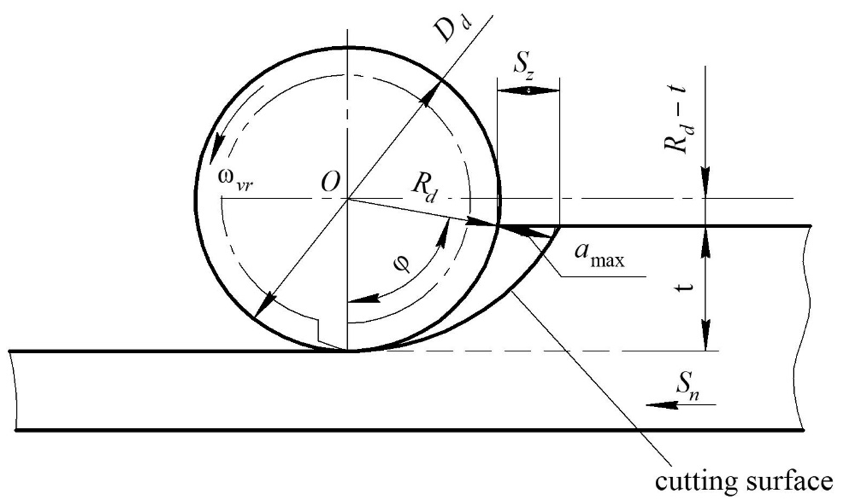
Since (Kumabe, 1979; Poduraev, 1985), cutting kinematics determines the shape and size of chips, then it is expedient to control the chip formation according to the method (Sergeev et al., 2009) – by changing the kinematic movements of the rotating multiple-cutting-edge tool through the forced controlled radial vibration. This approach is fundamentally new. According to this granulation method (Sergeev et al., 2009), movement patterns of the milling cutter teeth 1 (cutter diameter is D) are formed by combining three trajectories (Figure 1): cutting speed as a uniform rotation around the axis O0 with a frequency ωvr; uniform feed motion S; oscillatory feed motion forced in the radial direction with a frequency ωk and amplitude A (A = 2ρ) as a rotational movement of the eccentric 2 relative to Oe. As a rule, tool oscillations can be any, for example, if one uses (Sergeev et al., 2014), he/she has to consider the major property of treated material while making a mathematical model – namely, the shape stability typical for solids. In other words, the main qualitative difference between a solid, a liquid and gaseous media is that the solid media "remembers" all past impacts. Besides, the path of a penetrating element depends not only on its current location, but also on a number of its previous positions.

Figure 1
Scheme of chip formation with a vibrating cutting tool

As a result, we will have the interrupted cutting condition guaranteeing the separation of dispersed chips (Figure 2):

Figure 2– Scheme of chip formation

Figure 3 – Scheme of the changing positions of a cutting
plane under radial feed and oscillations

Figure 4 – Kinematics of grinding without radial oscillations

------

Figure 5 – Kinematics of grinding with radial oscillations

Figure 6 – Particle cross-section

Figure 7 – Facility diagram

4. Discussion

As the oscillation amplitude increases, the greatest value of the cut-off particle thickness increases. As the oscillation frequency decreases, the greatest value of the cut-off particle length increases.

Since mathematical models (1,15,17-20) allow us to measure the shape and size of dispersed particle hypersurface, we are able now to model and control the process of dispersion with a computer and modern software tools in real time (Sergeev et al., 2015).

The computer-based simulator of chip formation with specified shape and size through cutting is based on the mathematical logic apparatus, since our problem can be mathematically described as the process of finding constituents. Thus, problem to be solved involves the main fundamental factors affecting the cutting process. Secondly, we have had regard to the fact that shapes of particles cut off by the cutting edges (due to the influence of these factors) are complex related hypersurfaces and depend on whether there is (conjunction) a trace left by the previous cutting blade at the each moment of time or not (disjunction). In other words, mathematical model takes into account that each subsequent chip surface cut off by the i-th cutting blade has initial conditions, depending on the previous cut-off layers.

Figure 8 – Animated process of grinding a plate with a five-tooth mill

-----

Figure 9 – Animated process of particle formation with specified shape by the oscillatory mill movements

In the course of computer-based dispersion modeling, this program allows controlling the shape and size of dispersed particles in a wide range (Figure 10)

Figure 10 – Examples of particle shape control by changing the oscillation parameters

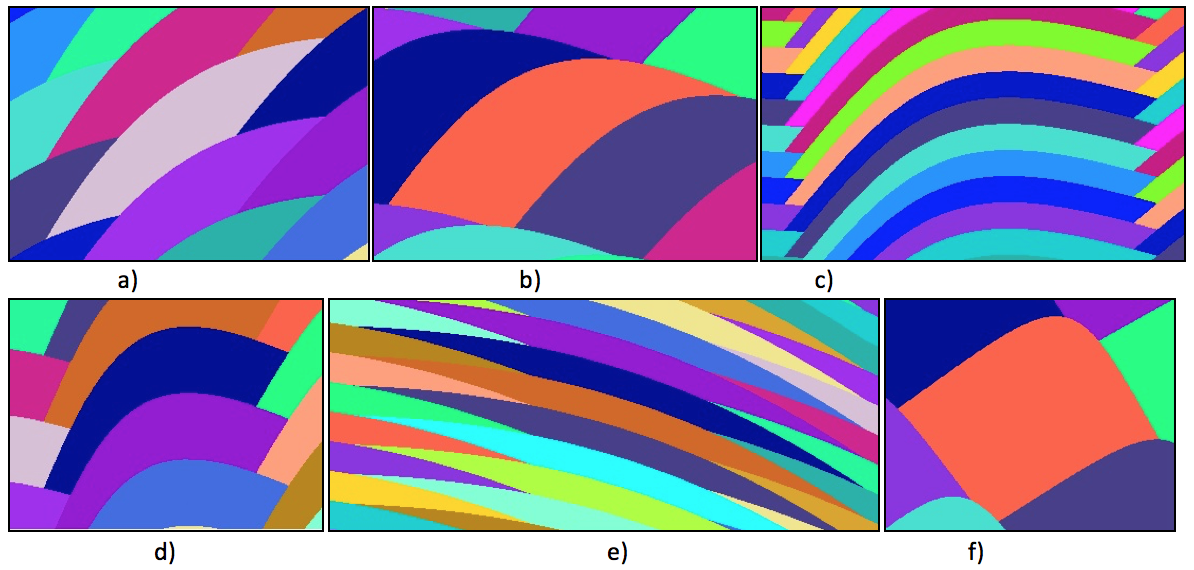
The control is carried out by changing the technological process parameters: forced oscillation amplitude of the mill and the ratio of rotation frequencies and its oscillations. The simulator allows not only measuring the sizes and volumes of dispersed particles, but also visualizing the entire cutting process (Figures 11 and 12).

Figure 11 – Granulation process report form. The first report sheet
(automatically generated when the simulation is complete)

Figure 12 – Granulation process report form. The second report sheet
(automatically generated when the simulation is complete)

5. Conclusion

Thus, obtained results have proved the principal possibility of forming cut-off layers of required size and shape by introducing forced oscillations of a rotating multiple-cutting-edge tool into the cutting area. In the future, this opportunity made it possible to implement a fundamentally new direction in processing metals and plastics – dimensional dispersion of materials, including waste.

The process of modeling dimensional dispersion by cutting allows controlling the size and shape of dispersed particles while their PSD stability increases, as well as determining its capabilities in regards to criteria.

The major conceptual basis is the practical implementation of the very process of dimensional dispersion, since the literary sources presented this concept only as a problem statement. Currently, dimensional mechanical dispersion is a fundamentally new direction, which is only being formed under the demand of powder and fiber producers, as well as under the demand of specialists engaged in industrial and household solid waste treatment. The existing dispersers work on the principle of "coffee grinder" and do not allow controlling the process. Therefore, it is important to conceptually change the attitude towards the dispersed particle formation. In other words, one has to treat it as the process of producing parts with metrological parameters: size and shape accuracy. Therefore, cutters and grinders have to be brought to the level of vibration disperser designs, which make it possible to meet these parameters. Their designs must also have the technological parameter tuning units. Obtained mathematical models make it possible to carry out the computer-based predictive modeling of dispersed particle formation. This opens the way to the creation of automatically-operated vibration dispersers for viscous media.

Acknowledge

South Ural State University is grateful for financial support of the Ministry of Education and Science of the Russian Federation (grant No 9.7960.2017/BP).

References

Balaykin, A. V., Smelov, V. G., Chempinskiy, L. A. (2012). Application of additive technologies for creating combustion chamber parts. Bulletin of Samara University. Aerospace technology, tech-nology and engineering. no. 3–2 (34), 47–52.

Chumanov, I. V., Chumanov, V. I., & Anikeev, A. N. (2015). Investigating the effect of carbide disperse particles on hardness and wear resistance of experimental materials in cast and deformed conditions. Indian Journal of Science and Technology, 8(34).

Chumanov, I. V., Kareva, N. T., Chumanov, V. I., & Anikeev, A. N. (2012). Study and analysis of the structural constituents of billets hardened by fine-grained particles and formed by centrifugal casting. Russian Metallurgy (Metally), 2012(6), 539-541.

Chumanov, I., Anikeev, A., & Chumanov, V. (2017, February). Reinforcement of the bulk crowns excavator technology by dispersion hardening of titanium carbide to increase wear resistance. In IOP Conference Series: Materials Science and Engineering (Vol. 179, No. 1, p. 012031). IOP Publishing.

Chumanov, V. I., Chumanov, I. V., Anikeev, A. N., & Garifulin, R. R. (2010). Hardening of the surface layers of a hollow billet formed by centrifugal casting. Russian Metallurgy (Metally), 2010(12), 1125-1128.

Gordeev, E. N., Sergeev, S. V., & Chumanov, I. V. (2010). Improvement of the processing of the wastes of nonferrous metals into high-quality secondary raw materials. Russian Metallurgy (Metally), 2010(12), 1173-1174.

Gordienko, V. P., Mustyatsa, O. N., & Kovaleva, G. N. (2016). The effect of combined dispersion of polyethylene and carbides on the structure and physicomechanical properties of composite materials. International Polymer Science and Technology, 43(7), T15.

Hamran, N., & Rashid, A. A. (2017). Effect of combination ultrasonic and ball milling techniques of commercial fillers dispersion on mechanical properties of natural rubber (NR) latex films. In AIP Conference Proceedings (Vol. 1865, No. 1, p. 040011). AIP Publishing.

Hayes, E., Cnuts, D., Fullagar, R., Pardoe, C., Clarkson, C., & Stephenson, B. (2014). Experimental replication of Australian grinding stone implements.

Kalpakjian, S., & Schmid, S. R. (2014). Manufacturing engineering and technology (p. 913). Upper Saddle River, NJ, USA: Pearson.

Kumabe, J. (1979). Vibration cutting—basic principle and application. Japan: Jikkyo Shuppan Books.

Lakirev, S. G., Sergeev, S. V., Gordeev, E. N., Reshetnikov, B. A., Zakirov, R. G. (2003). Sposob i ustroystvo izmel'cheniya materialov. Method and device for grinding materials. Patent RF 2213618, no. 2002102797/03; decl. 31.01.2002. No. 28. 56.

Lakirev, S. G., Sergeev, S. V., Reshetnikov, B. A., Zakirov, R. G., Gordeev, E. N. (2003). Research and improvement of technology of manufacturing of products from a concrete mix. Bulletin of South Ural State University. Ser. «Construction and architecture». vol. 2, no.7 (23), 32–34.

Ouelaa, N., Younes, R., Hamzaoui, N., & Djebala, A. (2017). Experimental Study of Real Gear Transmission Defects Using Sound Perception. In Applied Mechanics, Behavior of Materials, and Engineering Systems (pp. 267-274). Springer International Publishing.

Parveen, S., Rana, S., & Fangueiro, R. (2013). A review on nanomaterial dispersion, microstructure, and mechanical properties of carbon nanotube and nanofiber reinforced cementitious composites. Journal of Nanomaterials, 2013, 80.

Poduraev, V. N. (1985). Tekhnologii︠a︡ fiziko-khimicheskikh metodov obrabotki. Mashinostroenie.

Şahin, Y., & Yalcinkaya, S. (2016). Application of Taguchi Technique to Surface-Grinding of Mold Steel. Delta, 3(2.3051), 0-6546.

Salernitano, E., Migliaresi C. (2003). Composite materials for biomedical applications: a review Journal of applied biomaterials & biomechanics. JABB. Jan-Apr;1(1). 3-18.

Sandalov, V. M., & Sergeev, Y. S. (2012). Dynamic model of switched reluctance vibratory drive. Russian Electrical Engineering, 83(8), 432-435.

Sergeev S. V., Gordeev E. N. (2009). Recycling of composite materials based on metal. Safety in Technosphere, 2009, no. 2, 38–40.

Sergeev, S. V., Gordeev, E. N. (2010). Improvement of the process of grinding of metal and plastic wastes during their processing. Chelyabinsk, South Ural St. Univ. Publ. 110.

Sergeev, S. V., Gordeev, E. N., Sergeev, Yu. S., Sahautdinov, I. R., Gogolev, V. P., Schepin, M. A. (2011). Program for calculating and modeling chip elements for size grinding on vibration milling machines. Сertificate of state registration of a computer program 2011617667, no. 2011615885; decl. 03.08.2011.

Sergeev, S. V., Reshetnikov, B. A., Gordeev, E. N., Sergeev, Yu. S. (2009). Method for grinding viscous materials. Patent RF 2365469, no. 2007136686/02; decl. 04.10.2007. No. 24. 14.

Sergeev, S. V., Reshetnikov, B. A., Gordeev, E. N., Sergeev, Yu. S., Gogolev, V. P., Zakirov, R. G., Mikryukov, A. A., Irshin, A. V. (2014). Method of excitation of oscillations. Patent RF 2533743, no. 2013121307/28; decl. 07.05.2013. No 32. 12.

Sergeev, S. V., Sergeev, Yu. S., Shelegov, A. A., Karpov, G. E., Egorov, S. I. (2016). Simulator of the forming of chip elements of a given shape and size. Сertificate of state registration of a computer program 2016616657, no. 2016613942; decl. 21.04.2015.

Sergeev, Yu. S. (2011). Drives of vibration machines based on switched reluctance drive. Abstract of сand. sci. diss. Chelyabinsk, 22.

Sergeev, Yu. S., Sergeev, S. V., Karpov, M. A. (2016). Results of search design of devices for extraction of metal-containing waste from metallurgical slags. Nauka YUUrGU. Materialy 68-y nauch-noy konferentsii. Science of SUSU. Materials of the 68th scientific conference. 1209–1213.

Sumelka, W., Zaera, R., & Fernández-Sáez, J. (2016). One-dimensional dispersion phenomena in terms of fractional media. The European Physical Journal Plus, 131(9), 320.

Svinin, V. M., Samorodov, P. A. (2016). Investigation of the dynamic stability of a heavy technological system in the face milling with the variable step of the tool torques. Mechanics of the XXI century. № 15. pp. 167-173.

Webster, J. G., & Eren, H. (Eds.). (2014). Measurement, instrumentation, and sensors handbook: spatial, mechanical, thermal, and radiation measurement (Vol. 1). CRC press.

1. South Ural State University, Ave. Lenin, 76, Chelyabinsk, 454080, Russia.

2. South Ural State University, Ave. Lenin, 76, Chelyabinsk, 454080, Russia.

3. South Ural State University, Ave. Lenin, 76, Chelyabinsk, 454080, Russia.

Contact E-mail:  kseniabadz@gmail.com