

Vol. 38 (Nº 31) Año 2017. Pág. 27
Héctor Alonso OLIVARES Aguayo 1; Christian BUCIO Pacheco 2; Gabriel Alberto AGUDELO Torres 3; Luis Ceferino FRANCO Arbeláez 4; Luis Eduardo FRANCO Ceballos 5
Recibido: 27/01/2017 • Aprobado: 05/03/2017
3. Análisis y aplicación de resultados
RESUMEN: En este artículo se analizan empresas mexicanas del sector vivienda (ARA, HOMEX y URBI), considerando una muestra de dos años con precios históricos diarios (2011-2013). Se realiza un análisis de portafolios bivariados mediante una diversificación naive comparando el Valor en Riesgo (VaR) calculado con tres métodos Delta Normal, Histórico y Monte Carlo contra el VaR calculado mediante cópulas elípticas (Gaussiana y t-Student) con un nivel de confianza del 95%. Por último, se ejecuta el método de backtesting mediante la prueba de Kupiec, determinando que el VaR Cópula t-Student es la medida de riesgo más adecuada para todos los portafolios bivariados de las empresas analizadas. |
ABSTRACT: This paper analyzes Mexican companies in the housing sector (ARA, Homex and Urbi), considering a sample of two years with daily historical prices (2011-2013). It is performed an analysis of bivariate portfolios by a naive diversification comparing the Value at Risk (VaR) calculated with three methods Delta Normal, Historical and Monte Carlo, against the VaR calculated using elliptic copulas (Gaussian and t-Student) with a confidence level of 95%. Finally the method of backtesting is performed by the Kupiec test, determining that the t-Student copula VaR risk measure is most suitable for all bivariate portfolios of the companies analyzed. |
El Valor en Riesgo (VaR, por sus siglas en inglés) es un concepto desarrollado en el ámbito financiero de la administración de riesgo, el cual proviene de la necesidad de cuantificar con un determinado nivel de confianza el monto de pérdida máxima esperada que un portafolio enfrentará en un período predefinido de tiempo (Jorion, 2007).
La principal característica del porqué el VaR se ha convertido en la metodología estándar en la medición del riesgo de mercado, es su fácil implementación, flexibilidad e interpretación. No obstante, el VaR es un concepto controvertido, debido principalmente a los diversos métodos utilizados para su cálculo, diferentes valores obtenidos y la posibilidad de que la cuantificación del riesgo de mercado genere una subestimación del VaR. En esencia el VaR no es más que una cantidad, expresada en unidades monetarias o en términos porcentuales. Dicha cantidad tiene la característica de que puede ser especificada mediante diversas metodologías, es por ende que no sólo es necesario especificar los parámetros referidos sino también el método de estimación empleado en su cálculo.
Para el cálculo del VaR, previamente se requiere calcular los rendimientos del portafolio, después se determinan las pérdidas y ganancias del mismo, tradicionalmente y por simplicidad se supone que los rendimientos son gaussianos, pero la evidencia empírica muestra que éstos no necesariamente se comportan así. De este modo es que se han creado modelos con supuestos más realistas para medir de manera más eficiente las pérdidas y ganancias de un portafolio.
Basilea II recomienda el VaR como la medida de riesgo de mercado para poder establecer el umbral, a partir del cual una empresa puede tener la máxima pérdida dada una inversión inicial en un horizonte de tiempo y con un nivel de confianza determinado, bajo condiciones normales de mercado. El VaR debería expresar de forma precisa la exposición al riesgo; sin embargo cuando la actividad en los mercados financieros es de alta volatilidad; el VaR es más complejo de medir.
Las medidas de VaR tradicionales propuestas por el Comité de Basilea son: VaR Histórico, VaR Paramétrico y VaR Monte Carlo. Sin embargo, estos modelos suelen ser adecuados solo en condiciones de volatilidad estable, por lo que es necesario analizar su comportamiento en condiciones adversas (alta volatilidad), teniendo en cuenta los problemas de modelación en sesgo y curtosis (Forsey, 2001 y Chen, 2012). Estos problemas son relevantes, ya que en situaciones de alta volatilidad en los precios de los activos financieros; el VaR puede subvaluar las pérdidas potenciales de un portafolio, lo cual podría generar inclusive hasta quebrantos de la propia empresa. Por lo que es importante llevar a cabo pruebas que permitan la medición adecuada del riesgo de mercado. Más aún, una alternativa para validar el VaR del portafolio es la prueba de backtesting de Kupiec (1995), la cual consiste en comparar las pérdidas y ganancias reales contra las estimadas por el VaR.
Por otro lado, la modelación de fenómenos económico-financieros mediante cópulas ha sido utilizada en múltiples aplicaciones, entre las que destacan el análisis del riesgo actuarial y el análisis de riesgo financiero. Por ejemplo: Frees y Valdez (1998) muestran el uso de cópulas en el análisis de riesgo actuarial; mientras que Embrechts, McNeil y Straumann (2002) muestran las bondades del uso de cópulas en finanzas. Varios debates metodológicos y empíricos sobre el uso de cópulas pueden consultarse en Cherubini, Luciano y Vecchiato (2004); Rockinger y Jondeau (2001); Embrechts, Höing y Juri (2003); y Chen y Fan (2002).
En Torres y Olarte (2009) se analiza la estimación del VaR mediante cópulas. Embrechts, Höing y Puccetti (2005) aplican cópulas para generar diversos escenarios de VaR para el peor de los casos. En Rank (2007) se muestra la viabilidad del uso de cópulas en el cálculo del VaR por el método de Simulación Monte Carlo.
La hipótesis de este artículo es que los modelos VaR mediante cópulas elípticas son una medida de riesgo más viable que los modelos VaR tradicionales respecto a la subestimación del riesgo de mercado.
Por lo anterior se realiza un comparativo entre los modelos de VaR considerando cópulas elípticas bivariadas (Gaussiana y t-Student) contra los modelos de VaR tradicional también bivariados, considerando el nivel de confianza del 95% y una diversificación naive. El criterio de validación del VaR será con la metodología de backtesting mediante la prueba de Kupiec (1995). El backtesting es una metodología que valida la precisión del VaR. Esta metodología es calculada usando el número de excepciones observadas en un intervalo de tiempo.
La presente investigación está organizada como sigue. En la siguiente sección se explican las metodologías de los modelos de VaR Histórico, VaR Paramétrico, VaR Monte Carlo y VaR con cópulas elípticas. En la Sección 3 se presentan y discuten los resultados obtenidos, se concluye en la Sección 4. Asimismo en un Apéndice se muestran gráficamente los portafolios bivariados con riesgo moderado (HOMEX-ARA y URBI-ARA) y el portafolio con riesgo alto (HOMEX-URBI) y finalmente se presentan las referencias.
En general, los métodos de simulación modelan la distribución de una variable que puede ser el precio de un activo como una acción, mediante la generación de un conjunto de escenarios simulados de valores posibles de esa variable. En el enfoque de VaR Histórico se generan escenarios mediante la aplicación de cambios en los factores de riesgo de un periodo histórico (definido por el usuario con fechas de inicio y final) a niveles de factores de riesgo actuales, para después revalorar cada activo con los nuevos niveles de factor de riesgo (J.P. Morgan Bank, 1996). No hay supuestos sobre distribución (por ejemplo, gaussiana o log-gaussiana) para ninguno de los factores de riesgo o de precios. En cambio, se trabaja con la distribución de los factores de riesgo subyacente en el período de tiempo determinado. La desventaja principal de esta metodología es que no toma en cuenta la variación del riesgo a través del tiempo y en situaciones de alta volatilidad no estima de manera eficaz los valores extremos.
A continuación se muestra el algoritmo de simulación para el cálculo del VaR Histórico utilizado en este artículo:



En 1994 J.P. Morgan mediante su metodología RiskMetrics introduce lo que se conoce como el método de VaR Delta Normal; el cual es un modelo paramétrico que está fundamentado en la teoría de portafolio de Markowitz (1952) de media-varianza.
El problema de optimización en media-varianza resuelto por Markowitz proporcionó la base para el cálculo del VaR, este método está basado en el supuesto de rendimientos normales, es decir, para su cálculo se supone que los rendimientos son independientes e idénticamente distribuidos, con distribución gaussiana y con volatilidades estables a través de un horizonte temporal determinado.
El VaR Delta Normal se determina de la siguiente manera:

La simulación de Monte Carlo fue desarrollada originalmente para la valuación de derivados (Glasserman, 2003), y su uso se ha extendido al cálculo del Valor en Riesgo (VaR). Constituye un método paramétrico porque se supone que un proceso estocástico conduce la dinámica de los activos subyacentes. Los parámetros de tal proceso estocástico se pueden estimar a partir de datos históricos o calibrados con información de mercado. Por último, se simulan trayectorias de precios de los activos y luego se genera una distribución de los valores del portafolio en su caso. Este método considera variaciones a través del tiempo, captura de colas pesadas y valores extremos. Para implementar el modelo se necesita de una estructura computacional eficiente.
La metodología del VaR Monte Carlo es la siguiente:

Para simular las trayectorias de precios, para el caso bivariado, se utiliza el siguiente procedimiento:

El VaR con cópulas elípticas pretende estimar las colas gruesas de las distribuciones, obteniendo resultados más realistas y evitando así la subestimación del riesgo de mercado del portafolio.
De acuerdo con Romano (2002), Rank (2007) Fantazzini (2008), en este artículo se hace el uso de la estimación del VaR mediante simulación Monte Carlo con una adaptación a la teoría de cópulas.

Además, en los casos multivariados gaussiano y t-Student, cuando se usan cópulas con diferentes marginales, la estimación del VaR no es sencilla, ya que no es fácil utilizar fórmulas para obtener medias y volatilidades condicionales al VaR para las posiciones largas y cortas del portafolio. Sin embargo, el VaR puede ser estimado mediante simulación Monte Carlo.
Además, Giot y Laurent (2003) muestran que una elección de 100 000 simulaciones proporciona estimaciones precisas del cuantil.
Siguiendo este procedimiento por Monte Carlo, se genera un número suficiente de rendimientos con un día de anticipación ![]() para las dos empresas mediante la simulación de 100 000 rendimientos aleatorios con función de distribución acumulada correspondiente a la Ecuación (14). Y finalmente se revalúa el portafolio en el momento t. Entonces, la estimación del VaR está determinada por el p-ésimo cuantil empírico de la distribución del portafolio simulado de pérdidas y ganancias.
para las dos empresas mediante la simulación de 100 000 rendimientos aleatorios con función de distribución acumulada correspondiente a la Ecuación (14). Y finalmente se revalúa el portafolio en el momento t. Entonces, la estimación del VaR está determinada por el p-ésimo cuantil empírico de la distribución del portafolio simulado de pérdidas y ganancias.
Los pasos detallados del procedimiento para la estimación del p-ésimo cuantil empírico de la distribución del portafolio simulado de pérdidas y ganancias del VaR durante un período de tenencia de un día son los siguientes:



La metodología backtesting aplicada al VaR determina el número de excepciones encontradas contra el número de excepciones que deberían presentarse según una distribución determinada.

En este artículo se programaron mediante MatLab diversos modelos de VaR tradicionales (Delta Normal, Histórico y Monte Carlo) y modelos VaR con cópulas elípticas (Cópula Gaussiana y Cópula t-Student) al nivel de confianza del 95%. Esto significa que solamente el 5% de las veces, o 1 de 20 veces, o lo que es equivalente, una vez al mes con datos diarios, el rendimiento esperado del portafolio caerá más de lo que señala el VaR. Posteriormente se procede a analizar los resultados que se obtuvieron en dichos modelos; para ello se extrajo información diaria en los precios de las empresas a través de BLOOMBERG a partir del 29 de Julio de 2011 y hasta el 29 de Julio de 2013, los resultados se analizan mediante el método de backtesting aplicado a los diferentes tipos de VaR para los portafolios con riesgo moderado (HOMEX-ARA y URBI-ARA) y el portafolio con riesgo alto (HOMEX-URBI). Los cuales en general muestran una subestimación del riesgo de mercado por los modelos VaR tradicionales; mientras que el VaR Cópula t-Student se observa que es un modelo más adecuado, es decir, no subestima el riesgo de mercado para los tres portafolios analizados correspondientes a empresas del sector de vivienda en México. Dichos resultados son comprobados a través de la prueba de Kupiec la cual establece como límite de excepciones en el modelo, 20 excepciones, a un nivel de confianza del 95%, es decir, no se permite que el VaR estimado se encuentre por debajo de las pérdidas y ganancias reales del portafolio en 20 ocasiones o más, ya que, al ocurrir esto indicaría no ser un modelo VaR viable y por ende se estaría subestimando el riesgo de mercado. Lo cual generalmente puede ocurrir por la alta volatilidad en los precios de las empresas que conforman el portafolio.
Los precios y rendimientos de las empresas analizadas se observan en la Figura 1 y en la Figura 2:
Figura 1. Precios de las empresas (HOMEX, ARA, URBI).

Fuente: elaboración propia en Excel.
Figura 2. Rendimientos logarítmicos de las empresas (HOMEX, ARA, URBI).

Fuente: elaboración propia en Excel.
Las figuras anteriores muestran clusters de volatilidad en los precios de HOMEX y URBI, mientras que para ARA se tiene estabilidad; es decir, no se observan clusters de volatilidad debido a que éstos fueron en periodos anteriores al periodo de estudio de esta investigación. Por lo anterior desde un punto de vista gráfico definiremos al portafolio (URBI-ARA) como un portafolio con riesgo moderado, al portafolio (HOMEX-ARA) también como un portafolio con riesgo moderado, mientras que el portafolio (HOMEX-URBI) como un portafolio con riesgo alto; por lo cual es importante observar el comportamiento de éstos portafolios bivariados que consideran una diversificación naive, la cual consiste en otorgar el mismo porcentaje de inversión a cada activo del portafolio, es decir, se tiene una ponderación del 50% para cada empresa. En este artículo se supone una inversión de $3,000,000 de pesos mexicanos en cada portafolio. Entonces la inversión en cada empresa sería de $1,500,000 pesos mexicanos.
Asimismo, se realizó mediante el software R un análisis gráfico en los rendimientos de cada empresa. Las pruebas en cuantiles considerando un nivel de confianza de los 95%; dichas pruebas se pueden apreciar en la Figura 3, Figura 4 y Figura 5. Mientras que los gráficos de los histogramas se observan en la Figura 6, Figura 7 y Figura 8. En todas éstas se observa que en ningún caso los datos correspondientes a los rendimientos de las empresas analizadas tienen comportamiento gaussiano; las pruebas de cuantiles destacan problemas en las colas de la distribución; mientras que en los histogramas se observa leptocurtosis y asimetría en la distribución.
Figura 3: Prueba de cuantiles gaussianos para HOMEX al 95% de confianza.

Fuente: Elaboración propia mediante el software R.
Figura 4: Prueba de cuantiles gaussianos para ARA al 95% de confianza.

Fuente: Elaboración propia mediante el software R.
Figura 5: Prueba de cuantiles gaussianos para URBI al 95% de confianza.

Fuente: Elaboración propia mediante el software R.
Figura 6. Histograma de HOMEX.

Fuente: elaboración propia mediante el software R.
Figura 7. Histograma de ARA.

Fuente: Elaboración propia mediante el software R.
Figura 8. Histograma de URBI.

Fuente: Elaboración propia mediante el software R.
También se realizaron mediante el software R las pruebas estadísticas de bondad y ajuste de Kolmogorov-Smirnov, Cramer-von Mises y Anderson-Darling suponiendo como hipótesis nula comportamiento gaussiano para los rendimientos de cada empresa. Los resultados de estas pruebas se muestran en la Tabla 1, Tabla 2 y Tabla 3:
Tabla 1. Pruebas estadísticas de bondad y ajuste gaussiano para HOMEX.
Kolmogorov-Smirnov statistic |
0.1522152 |
p-value |
7.523e-11 |
Cramer-von Mises statistic |
4.1942235 |
p-value |
7.37e-10 |
Anderson-Darling statistic |
23.9198807 |
p-value |
2.2e-16 |
Fuente: Elaboración propia mediante el software R.
Tabla 2. Pruebas estadísticas de bondad y ajuste gaussiano para ARA.
Kolmogorov-Smirnov statistic |
0.07299961 |
p-value |
0.008005 |
Cramer-von Mises statistic |
1.04221841 |
p-value |
1.031e-09 |
Anderson-Darling statistic |
6.14808728 |
p-value |
3.309e-15 |
Fuente: Elaboración propia mediante el software R.
Tabla 3. Pruebas estadísticas de bondad y ajuste gaussiano para URBI.
Kolmogorov-Smirnov statistic |
0.1096271 |
p-value |
7.83e-06 |
Cramer-von Mises statistic |
2.2326931 |
p-value |
7.37e-10 |
Anderson-Darling statistic |
12.3452011 |
p-value |
2.2e-16 |
Fuente: Elaboración propia mediante el software R.
Para las tres pruebas estadísticas observadas se tiene que la hipótesis nula es H0: Los rendimientos son gaussianos. Como para todos los casos analizados se observa que el p-value es menor a .05 entonces se rechaza H0 y los rendimientos no son gaussianos. Por lo tanto los rendimientos no son ajustados por una distribución gaussiana.
Ampliando dichas pruebas estadísticas para los portafolios bivariados, se muestran los resultados obtenidos en las Tabla 4, Tabla 5 y Tabla 6:
Tabla 4. Pruebas estadísticas de bondad y ajuste gaussiano para el portafolio HOMEX-ARA.
Kolmogorov-Smirnov statistic |
0.1291 |
p-value |
1.998e-15 |
Cramer-von Mises statistic |
6.7569 |
p-value |
7.37e-10 |
Anderson-Darling statistic |
38.657 |
p-value |
2.2e-16 |
Fuente: Elaboración propia mediante el software R.
Tabla 5. Pruebas estadísticas de bondad y ajuste gaussiano para el portafolio URBI-ARA.
Kolmogorov-Smirnov statistic |
0.10227 |
p-value |
7.74e-10 |
Cramer-von Mises statistic |
4.0847 |
p-value |
7.37e-10 |
Anderson-Darling statistic |
23.169 |
p-value |
2.2e-16 |
Fuente: Elaboración propia mediante el software R.
Tabla 6. Pruebas estadísticas de bondad y ajuste gaussiano para el portafolio HOMEX-URBI.
Kolmogorov-Smirnov statistic |
0.12909 |
p-value |
1.998e-15 |
Cramer-von Mises statistic |
6.3762 |
p-value |
7.37e-10 |
Anderson-Darling statistic |
35.718 |
p-value |
2.2e-16 |
Fuente: Elaboración propia mediante el software R.
Para las tres pruebas estadísticas observadas se tiene que la hipótesis nula es H0: Los rendimientos de los portafolios bivariados son gaussianos. Como para todos los casos analizados se observa que el p-value es menor a .05 entonces se rechaza H0 y por lo tanto los rendimientos de los portafolios bivariados no son ajustados por una distribución gaussiana. Las gráficas de dichos portafolios bivariados se pueden observar en el Apéndice de este artículo.

Figura 9. Backtesting al 95% de confianza para el modelo VaR Histórico del portafolio HOMEX-ARA.

Fuente: Elaboración propia en Excel.
En la Figura 9 se muestran 19 excepciones por lo que el VaR Histórico con un nivel de confianza del 95% es un modelo viable para el portafolio HOMEX-ARA.
Figura 10. Backtesting al 95% de confianza para el modelo VaR Delta Normal del portafolio HOMEX-ARA.

Fuente: Elaboración propia en Excel.
En la Figura 10 se muestra 1 excepción por lo que el VaR Delta Normal con un nivel de confianza del 95% es un modelo viable para el portafolio HOMEX-ARA.
Figura 11. Backtesting al 95% de confianza para el modelo VaR Monte Carlo del portafolio HOMEX-ARA.

Fuente: Elaboración propia en Excel.
En la Figura 11 no se muestran excepciones por lo que el VaR Monte Carlo con un nivel de confianza del 95% es un modelo viable para el portafolio HOMEX-ARA.
Figura 12. Backtesting al 95% de confianza para el modelo VaR Cópula Gaussiana del portafolio HOMEX-ARA.
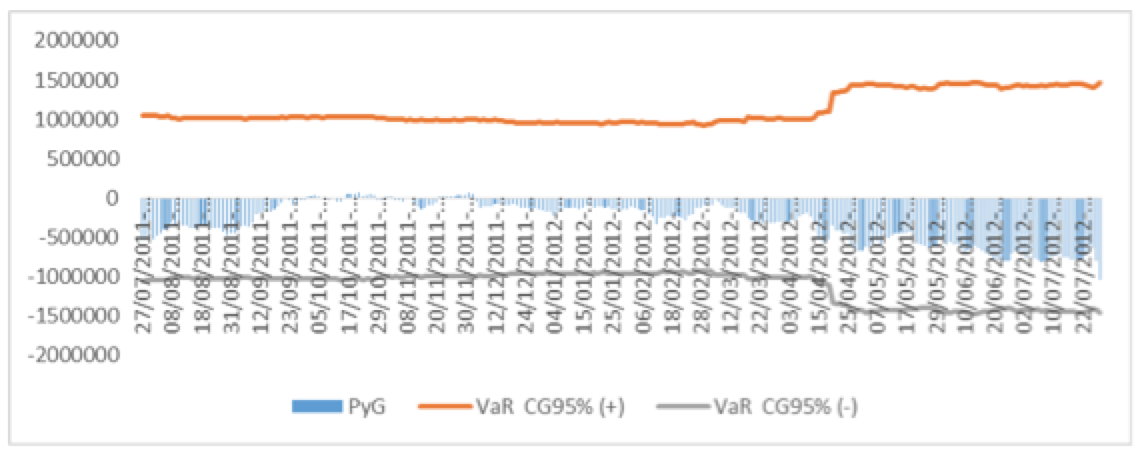
Fuente: Elaboración propia en Excel.
En la Figura 12 no se muestran excepciones por lo que el VaR Cópula Gaussiana con un nivel de confianza del 95% es un modelo viable para el portafolio HOMEX-ARA.
Figura 13. Backtesting al 95% de confianza para el modelo VaR Cópula t-Student del portafolio HOMEX-ARA.

Fuente: Elaboración propia en Excel.
En la Figura 13 no se muestran excepciones por lo que el VaR Cópula t-Student con un nivel de confianza del 95% es un modelo viable para el portafolio HOMEX-ARA.
Figura 14. Backtesting al 95% de confianza para el modelo VaR Histórico del portafolio URBI-ARA.

Fuente: Elaboración propia en Excel.
En la Figura 14 se muestran 154 excepciones por lo que el VaR Histórico con un nivel de confianza del 95% no es un modelo viable para el portafolio URBI-ARA.
Figura 15. Backtesting al 95% de confianza para el modelo VaR Delta Normal del portafolio URBI-ARA.
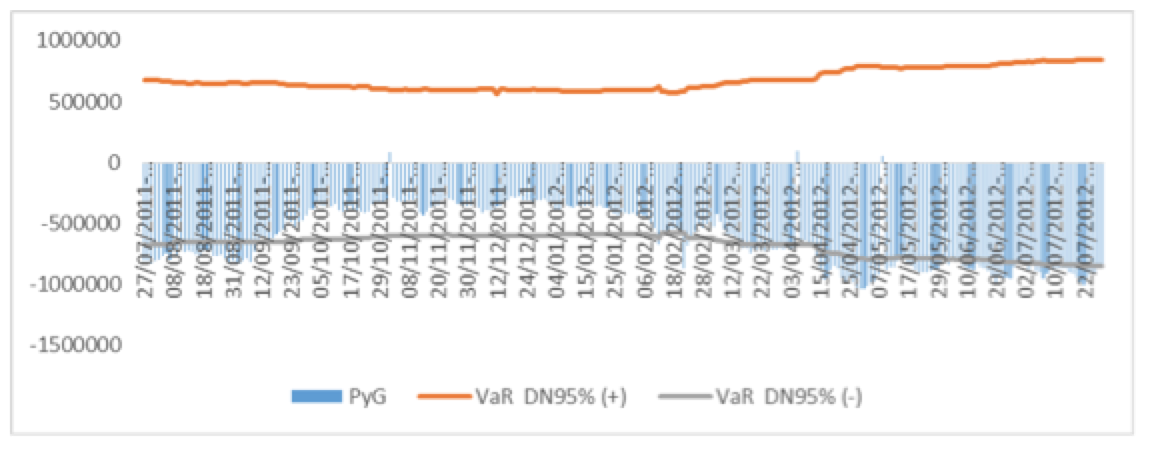
Fuente: Elaboración propia en Excel.
En la Figura 15 se muestran 126 excepciones por lo que el VaR Delta Normal con un nivel de confianza del 95% no es un modelo viable para el portafolio URBI-ARA.
Figura 16. Backtesting al 95% de confianza para el modelo VaR Monte Carlo del portafolio URBI-ARA.

Fuente: Elaboración propia en Excel.
En la Figura 16 se muestran 15 excepciones por lo que el VaR Monte Carlo con un nivel de confianza del 95% es un modelo viable para el portafolio URBI-ARA.
Figura 17. Backtesting al 95% de confianza para el modelo VaR Cópula Gaussiana del portafolio URBI-ARA.

Fuente: Elaboración propia en Excel.
En la Figura 17 se muestran 16 excepciones por lo que el VaR Cópula Gaussiana con un nivel de confianza del 95% es un modelo viable para el portafolio URBI-ARA.
Figura 18. Backtesting al 95% de confianza para el modelo VaR Cópula t-Student del portafolio URBI-ARA.
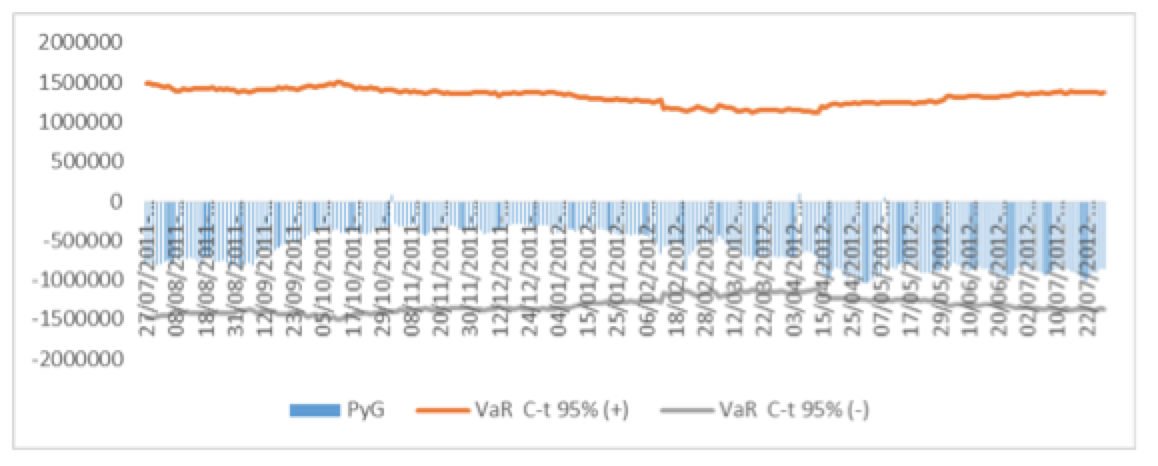
Fuente: Elaboración propia en Excel.
En la Figura 18 no se muestran excepciones por lo que el VaR Cópula t-Student con un nivel de confianza del 95% es un modelo viable para el portafolio URBI-ARA.
Figura 19. Backtesting al 95% de confianza para el modelo VaR Histórico del portafolio HOMEX-URBI.

Fuente: Elaboración propia en Excel.
En la Figura 19 se muestran 150 excepciones por lo que el VaR Histórico con un nivel de confianza del 95% no es un modelo viable para el portafolio HOMEX-URBI.
Figura 20. Backtesting al 95% de confianza para el modelo VaR Delta Normal del portafolio HOMEX-URBI.

Fuente: Elaboración propia en Excel.
En la Figura 20 se muestran 150 excepciones por lo que el VaR Delta Normal con un nivel de confianza del 95% no es un modelo viable para el portafolio HOMEX-URBI.
Figura 21. Backtesting al 95% de confianza para el modelo VaR Monte Carlo del portafolio HOMEX-URBI.
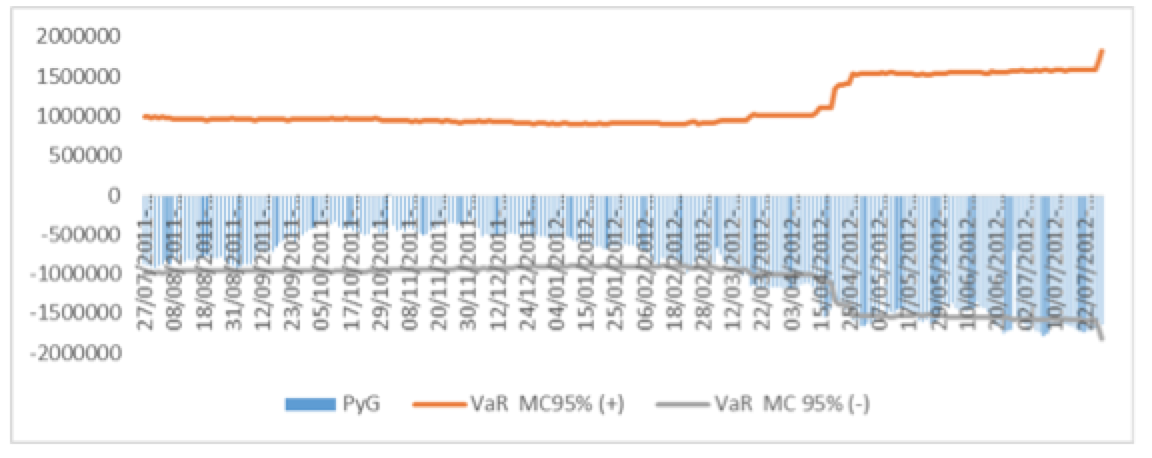
Fuente: Elaboración propia en Excel.
En la Figura 21 se muestran 71 excepciones por lo que el VaR Monte Carlo con un nivel de confianza del 95% no es un modelo viable para el portafolio HOMEX-URBI.
Figura 22. Backtesting al 95% de confianza para el modelo VaR Cópula Gaussiana del portafolio HOMEX-URBI.

Fuente: Elaboración propia en Excel.
En la Figura 22 se muestran 74 excepciones por lo que el VaR Cópula Gaussiana con un nivel de confianza del 95% no es un modelo viable para el portafolio HOMEX-URBI.
Figura 23. Backtesting al 95% de confianza para el modelo VaR Cópula t-Student para el portafolio HOMEX-URBI.
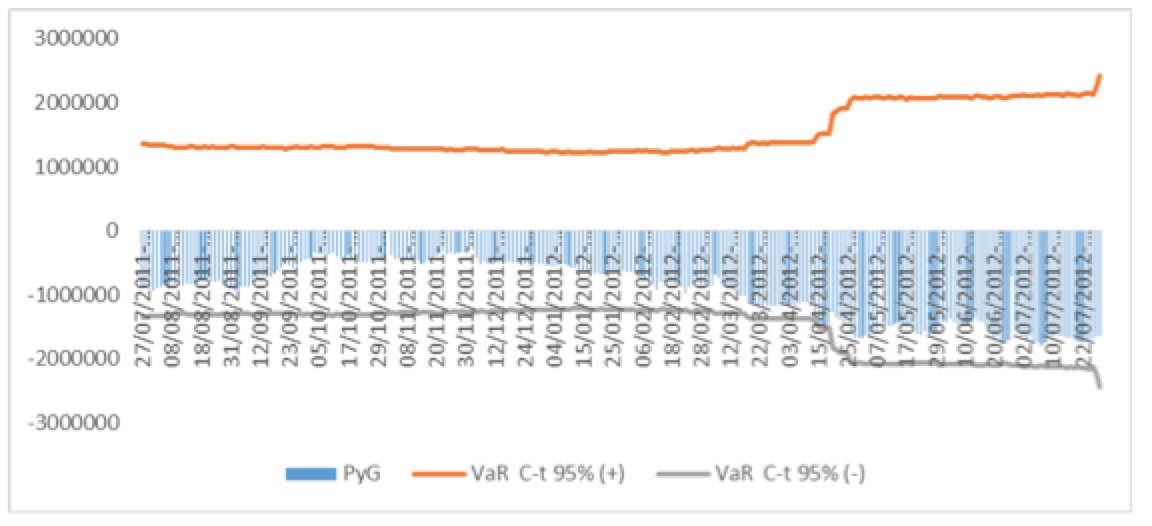
Fuente: Elaboración propia en Excel.
En la Figura 23 se muestran 2 excepciones por lo que el VaR Cópula t-Student con un nivel de confianza del 95% es un modelo viable para el portafolio HOMEX-URBI.
Actualmente la ingeniería financiera ha tenido avances notables en el desarrollo de metodologías para la resolución y modelación de problemas propios de las finanzas cuantitativas. Uno de estos avances es la medición del riesgo de mercado con metodologías alternativas basadas en cópulas, lo cual representa una manera de establecer una medición eficiente de riesgo del mercado.
En este artículo se han comparado varios tipos de VaR al nivel de confianza del 95%, observando que en general los modelos VaR tradicionales que se han considerado para analizar las pérdidas de los portafolios bivariados correspondientes a las empresas (HOMEX, URBI y ARA) subestiman el riesgo de mercado. La evidencia empírica a través del método de backtesting con un 95% de confianza muestra que para el portafolio con riesgo moderado (HOMEX-ARA) todos los modelos VaR son viables; sin embargo para el portafolio con riesgo moderado (URBI-ARA) los modelos de VaR tradicional VaR Histórico y VaR Delta Normal no son modelos de VaR viables, ya que, sobrepasan por más de 100 excepciones el número límite permitido por la prueba de Kupiec. Mientras que para el portafolio con riesgo alto (HOMEX-URBI), el cual es de mayor interés en este estudio al tener altas volatilidades en los precios de cada empresa, se observa que todos los modelos de VaR tradicionales (Histórico, Delta Normal y Monte Carlo) no son viables e incluso el VaR Cópula Gaussiana también falla; lo anterior porque dichos modelos exceden el límite de excepciones permitido por la prueba de Kupiec. Sin embargo, se observa que solamente el VaR Cópula t-Student es viable para el portafolio (HOMEX-URBI). Por lo cual se concluye que mediante la cópula elíptica t-Student se obtiene un modelo más adecuado y más robusto para modelar eventos extremos.
Por lo anterior la hipótesis de este artículo de investigación solo se cumple para los portafolios de riesgo moderado (HOMEX-ARA) y (URBI-ARA) ya que en ambos casos la evidencia empírica mostró viabilidad para el VaR por cópulas elípticas (Cópula Gaussiana y Cópula t-Student).
Es importante resaltar que para todos los tipos de portafolios bivariados analizados en esta investigación el modelo VaR Cópula t-Student fue viable, y por ende no subestimó el riesgo de mercado; dicha cópula es leptocúrtica lo que contribuye a capturar de manera eficaz los clusters de volatilidad. Lo anterior es consistente con el análisis estadístico realizado en R, tanto de manera gráfica como analítica mediante las pruebas de bondad y ajuste de Kolmogorov-Smirnov, Cramer-von Mises y Anderson-Darling, en las cuales se observó siempre el rechazo de rendimientos gaussianos de cada empresa y en cada portafolio bivariado.
Por último, aunque el VaR es una medida de riesgo estándar en la administración del riesgo de mercado, debido a su sencillez conceptual, la facilidad de su cálculo, y su aplicabilidad, debe ser complementada con un análisis de backtesting, tal y como lo recomienda el Comité de Basilea, lo cual permite al tomador de decisiones adoptar medidas de alerta temprana en ambientes de volatilidad extrema.
Basel Committee on Banking Supervision, Basel II: International Convergence of Capital Measurement and Capital Standards: A Revised Framework, www.bis.org/publ/bcbs107.pdf, 2004a.
Chen, J. (2012). “Postmodern Disaster Theory,” Working Paper, Michigan State University College of Law, Michigan.
Chen, Xiaohong y Fan, Y. (2002). “Evaluating density forecasts via the copula approach,” Working Paper, Vanderbilt University, US.
Cherubini, U.; Luciano, E. y Vecchiato, W. (2004). “Copula methods in finance,” John Wiley & Sons, UK.
Embrechts, Paul, Alexander McNeil, and Daniel Straumann (2002), “Correlation and Dependence in Risk Management: Properties and Pitfalls,” in Michael Dempster (Ed.), Risk Management: Value at Risk and Beyond, Cambridge University Press.
Embrechts, P.; Höing, A. y Juri, A. (2003), “Using Copula to bound the Value-at-Risk for functions of dependent risks,” Finance & Stochastics, vol. 7, no. 2, 145-167.
Embrechts. P.; Höing, A., Puccetti, G. (2005), “Worst VaR Scenarios,” Insurance. Mathematics and Economics, vol. 37, no. 1, pp. 115-134.
Fantazzini, D. (2008), “Dynamic Copula Modelling for Value at Risk”, Frontiers in Finance and Economics, vol, 5, no. 2, pp. 72-108.
Forsey, H. (2001), “The Mathematician’s View: Modelling Uncertainty with the Three Parameter Lognormal,” in Sortino, F., Satchell, S. (Eds.) Managing Downside Risk in Financial Markets, Butterworth-Heinemann, Oxford, UK, pp. 51-58.
Frees, Edward, and Emilio Valdez (1998), “Understanding Relationships Using Copulas,” North American Actuarial Journal, vol.2, no. 1, pp. 1-25.
Giot, P. & Laurent, S. (2003), “Market Risk in Commodity Markets: A VaR Approach,” Energy Economics, vol. 25, no. 5, pp. 435-457.
Glasserman, Paul (2003). Monte Carlo methods in financial engineering, Springer-Verlag, NewYork.
Jorion, P. (2007). Value at Risk: The New Benchmark for Managing Financial Risk. Third Edition. McGraw-Hill.
J. P. Morgan Bank (1996). RiskMetrics Technical Manual, New York.
Kupiec, P. (1995). “Techniques for Verififyng the Accuracy of Risk Measurement Models,” Journal of Derivatives, vol. 3, pp.73-84.
Markowitz, Harry M. (1952). “Portfolio Selection”, Journal of Finance, vol. 7, no. 1, pp. 77-91.
Rank, J. (2007), “Copulas: From theory to application in finance,” Risk Books, UK.
Rockinger, M. y Jondeau, E. (2001), “Conditionl dependency of financial series: an application of copulas,” Les Cahiers de Recherche, vol. 723, HEC Paris.
Romano C. (2002), “Applying Copula Function to Risk Management’, Working Paper, University of Rome, La Sapienza.
Torres, G. y Olarte A. (2009), “Valor en riesgo desde un enfoque de cópulas,” AD-MINISTER Universidad EAFIT, vol.15, 113-136.
Figura A1. Rendimiento del portafolio HOMEX-ARA.

Fuente: Elaboración propia mediante el software R.
-----
Figura A2. Rendimiento del portafolio URBI-ARA.
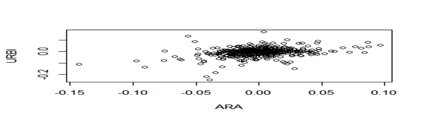
Fuente: Elaboración propia mediante el software R.
----
Figura A3. Rendimiento del portafolio HOMEX-URBI.

Fuente: Elaboración propia mediante el software R.
1. Escuela Superior de Economía, Instituto Politécnico Nacional. Correo electrónico: hectorlivares@hotmail.com
2. Unidad Académica Profesional Huehuetoca, Universidad Autónoma del Estado de México. Correo electrónico: cbuciop@uaemex.mx
3. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM. Correo electrónico: albertoagudelo@itm.edu.co
4. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM. Correo electrónico: lfranco@itm.edu.co
5. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM. Correo electrónico: lefranco@itm.edu.co