 HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN
HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN Espacios. Vol. 37 (Nº 20) Año 2016. Pág. 13
Eduardo MINGA 1; Alexandre Florindo ALVES 2; José Luiz PARRÉ 3
Recibido: 13/03/16 • Aprobado: 23/04/2016
RESUMO: Este artigo analisa o impacto de políticas monetárias nos EUA sobre três das commodities agrícolas mais consumidas no mundo: a soja, o trigo e o milho. O intuito é verificar se movimentos de afrouxamento monetário nos EUA causam movimentos especulativos nessas commodities de maneira a elevar seus preços para níveis significativamente superiores àqueles condizentes com os seus fundamentos, eventualmente levando pessoas de baixíssima renda a passar fome. Para a análise empírica foram utilizados dados de 1980 a 2014, utilizando-se como método econométrico um modelo VAR e suas ferramentas de decomposição de variância e funções impulso-resposta. Os resultados verificados indicam que as commodities analisadas sofrem pouca influência de variáveis monetárias, apresentando respostas de maior magnitude em relação às suas congêneres. Desta forma, verificam-se evidências de que movimentos especulativos frente ao enfraquecimento do dólar pouco influenciam a dinâmica do preço das commodities analisadas. |
ABSTRACT: This paper analyzes the impact of monetary policies in the US on three of the most consumed agricultural commodities in the world, soybeans, wheat and corn. The purpose is to verify if the monetary easing movements in the US cause speculation in these commodities in order to raise their prices to levels significantly above those consistent with its fundamentals, eventually leading to very low income people to starve. For the empirical analysis, we used 1980-2014 data, using as econometric method a VAR model and tools of variance decomposition and impulse response functions. The verified results indicate that the analyzed commodities suffer little influence of monetary variables, with higher magnitude responses of their counterparts. Thus, there is evidence that speculation against the dollar weakening slightly influence the dynamics of the price of commodities analyzed. |
Dentro do universo das commodities, um de seus subgrupos que gera maiores debates econômicos e políticos é o das commodities agrícolas. Longe de querer minimizar a importância de outros tipos, como minerais ou combustíveis, as agrícolas têm o diferencial de impactar diretamente em questões de grande apelo público como a fome e a pobreza. Por exemplo, o World Bank (2008) aponta que no ano de 2008 o número de pessoas extremamente pobres aumentou entre 130 e 155 milhões, em parte devido à alta das commodities agrícolas.
In general, higher food prices have had a more pronounced effect on poverty, because households in poor countries spend 50 percent or more of their income on food and only 10 percent on fuel [...] the poverty impacts are likely to be more significant because the demand for food is more inelastic than house hold demand for fuels, because the former can be replaced by biomass. (WORLD BANK, 2008, p. 11).
Além das implicações inerentes ao bem-estar social, trabalhos como o de Arezki e Bruckner (2011) ressaltam o impacto negativo que altas nos preços dos alimentos provocam sobre as instituições democráticas em países de baixa renda. Fatores como estes tornam a dinâmica de preços das commodities agrícolas um objeto de estudo de grande relevância.
Outro fator a se considerar, é a existência de vasta literatura apontando um relativo consenso de que em épocas marcadas pela incerteza quanto ao valor futuro da moeda, commodities passam a ser vistas como um porto seguro para a preservação da riqueza, como por exemplo, em Cooper e Lawrence (1975). Em geral, esses cenários costumam ser observados em períodos de política monetária frouxa, como se observou nos EUA em grande parte da primeira década do século XXI, culminando com um boom de commodities. Porém, quais commodities são mais visadas como forma de proteção e/ou especulação em momentos de enfraquecimento da moeda, é um ponto sobre o qual há divergências.
Historicamente o ouro é visto como uma das mais tradicionais reservas de valor, inclusive pelo seu histórico milenar de uso como moeda. Já em relação às commodities agrícolas, não existe um consenso. Alguns autores como Masters (2008 e 2009) e Paul e Wahlberg (2008) advogam a favor da existência de uma grande demanda especulativa por commodities agrícolas afetando significativamente os seus preços. Por outro lado, os estudos econométricos de Etienne, Irwin, Garcia (2014) e Natanelov et al. (2011), atribuem a alta das commodities agrícolas a outros fatores não relacionados a especulação financeira.
Pelo que foi exposto, este trabalho busca realizar um estudo empírico sobre os efeitos que políticas monetárias na maior economia do mundo, os EUA, causam no ouro e em três das principais commodities agrícolas do mundo, a soja, o trigo e o milho[4]. A abordagem proposta é analisar os impactos da taxa de juros base e dos agregados monetários M1 e M2 da economia americana, para as quatro commodities selecionadas. Desta maneira, a análise empírica será empreendida utilizando a modelagem de vetores autorregressivos (VAR) e seus instrumentais estatísticos de decomposição de variância e funções impulso-resposta. A justificativa para a utilização desta metodologia se dá pelo fato dela permitir a análise da interação dinâmica das variáveis, sem que se assuma a priori endogeneidade de alguma delas. Assim sendo, espera-se uma resposta do ouro frente às variáveis monetárias condizente com os inúmeros trabalhos que o apontam como um porto seguro em termos de reserva de valor. Posteriormente, a partir deste resultado, pretende-se comparar os resultados da soja, trigo e milho com o do ouro, para verificar se estas commodities possuem comportamento similar, caracterizando-as como ativos atraentes para quem deseja especular contra o dólar, ou não.
Este trabalho se estrutura em quatro partes. Primeiramente, esta introdução e a seguir uma breve revisão de literatura sobre os temas abordados neste artigo. Na seção 3 é apresentada a análise empírica, e por fim, a seção 4 é composta pelas considerações finais.
A literatura sobre os temas tratados neste trabalho, ou seja, especulação, commodities agrícolas, ouro e política monetária, são vastos, entretanto, são raros os estudos que os abordem de forma conjunta. Dessa maneira, uma revisão completa e exaustiva de cada um desses tópicos foge completamente do escopo deste artigo. Assim sendo, esta seção visa apresentar alguns conceitos a serem utilizados ao longo do artigo e apresentar um conjunto selecionado, e reconhecidamente limitado, de contribuições referentes aos assuntos abordados, para melhor posicionar o leitor na discussão.
Conforme preconiza a teoria econômica tradicional, o preço de um bem em um ambiente de mercado é determinado pela intersecção entre oferta e demanda. Desta maneira, podemos definir como demanda especulativa a parcela da demanda total que visa apenas obter lucro com a valorização futura do bem.
Em períodos de afrouxamento monetário é natural que o comportamento especulativo entre os agentes se torne mais frequente. Tudo mais constante, um aumento contínuo na quantidade de moeda na economia deprecia o seu poder de compra ao longo do tempo. Isso incentiva os agentes a investirem seus ativos líquidos em algo que ao menos cubra ou supere esse potencial de desvalorização. Além disso, essa maior disponibilidade de moeda reduz os juros, o que barateia o custo de empréstimos para agentes que desejam alavancar posições especulativas (WHITE, 2012, p. 36). Em termos práticos, como veremos na seção de análise empírica, podemos entender como um sinal de demanda especulativa respostas consideráveis no preço de um bem em relação a variáveis de monetárias.
No contexto ao qual este artigo se refere, o foco será a política monetária americana. Pois o seu afrouxamento, pelo fato do dólar ser a moeda de reserva global, tem potencial de desencadear movimentos especulativos por todo o mundo. Como mostram Fawley e Juvenal (2011) e White (2012), existe uma correlação muito evidente entre uma política monetária americana frouxa e um aumento no preço das commodities. Desta forma, o objetivo deste trabalho é verificar se existe um fator relevante de demanda especulativa influenciando o preço das commodities agrícolas selecionadas.
Etienne, Irwin, Garcia (2014) estudam o comportamento dos preços de contratos futuros da soja, milho e trigo, no período entre 2004 e 2013. Os resultados encontrados indicam que os preços destes mercados são guiados prioritariamente por seus fundamentos e que forças especulativas têm pouco efeito ou até mesmo efeitos negativos sobre estes preços.
Mitchell (2008) busca investigar os principais determinantes da alta que se observou no preço dos alimentos no período de 2002 a 2008, analisando fatores como a crescente produção de biocombustíveis, a fraqueza do dólar no período e o aumento nos custos de produção. A conclusão deste trabalho foi de que a alta no período foi causada por uma confluência de fatores, mas que o principal deles foi o aumento da produção de biocombustíveis nos EUA e UE.
Natanelov et al. (2011) realizam um estudo sobre relações de cointegração entre os preços de mercados futuros do petróleo, uma série de commodities agrícolas e o ouro. Sua principal conclusão é de que mercados futuros amadurecidos e bem estabelecidos de commodities agrícolas se movimentam de forma conjunta com o preço do petróleo no longo prazo.
Masters (2008 e 2009) é afirma que a especulação financeira com commodities agrícolas provoca distorções e booms infundados nestes mercados, levando pessoas a passar fome, "Wall Street should be prevented from gambling on hunger" (MASTERS, 2009, p. 2). Paul e Wahlberg (2008) defendem um ponto de vista similar, ressaltando os efeitos desestabilizadores da atividade especulativa. Um ponto em comum nestes trabalhos é a ênfase na crítica aos especuladores e à carência de análise estatística que corrobore com os argumentos. Masters (2008 e 2009) se resume a apresentar alguns dados em tabelas e gráficos, mas sem aplicar nenhuma modelagem formal a eles, enquanto Paul e Wahlberg (2008) se resumem à retórica.
Quanto ao comportamento do ouro em relação à política monetária, Barsky e Summers (1985) mostram a existência de uma relação inversa entre taxa de juros real e o preço do ouro. Bordo e Wheelock (2004) em seu trabalho que analisa o impacto de políticas monetárias sobre o preço de ativos, ressaltam que estas impactam primeiramente em commodities como o ouro, antes de afetar o nível geral de preços. Frankel (2008) enfatiza o papel do preço do ouro e outras commodities minerais como indicadores de expectativas de inflação futura, por estes se moverem mais rápido do que os preços de bens e serviços.
Como método de análise empírica, o artigo utilizará um modelo VAR (Vector Autoregressive). Sua escolha se justifica pela necessidade de analisar as interações dinâmicas entre as variáveis selecionadas, sem a necessidade de se estabelecer a priori quais são as variáveis endógenas e exógenas do modelo. Como argumenta Lütkepohl (2005, p. 66):
If economic theories are not available to specify the model, statistical tools must be applied. In this approach, a fairly loose model is set up which does not impose rigid a priori restrictions on the data generation process. Statistical tools are then used to determine possible constraints. VAR models represent a class of loose models that may be used in such an approach.

Neste modelo, a rigor, o termo de erro deve obedecer às propriedades de ruído branco independente, o que indica que ele é uma boa representação do processo gerador de dados. Entretanto, como ressalta Lütkepohl (2005, p. 157), "if, for example, forecasting is the objective, it may not be of prime importance whether the residuals are really white noise as long as the model forecasts well". Desta maneira, no decorrer do trabalho, não faremos maiores discussões sobre o termo de erro e assumiremos que o modelo proposto está bem especificado para os fins que ele se propõe.
A análise empírica baseia-se em séries temporais mensais, no período que se estende de novembro de 1980 a outubro de 2014. A escolha desse período se deve única e exclusivamente ao fato dele ser o de maior duração até os dias de hoje, sem falta de observações, para as variáveis escolhidas. As variáveis a serem utilizadas nas estimações para o período selecionado são:
ffr: Federal Funds Rate – A taxa de juros que os bancos ligados ao Federal Reserve System cobram uns dos outros por empréstimos overnight.
m1: Agregado monetário M1 dos EUA – Consiste no montante de moeda em espécie retida pelo setor não bancário, depósitos à vista e traveler's checks.
m2lm1: Agregado monetário M2 menos o M1 dos EUA – O M2 consiste no M1 acrescido de depósitos de poupança, depósitos a prazo inferiores a US$ 100.000,00 e saldos em fundos mútuos do mercado monetário de varejo. Desta maneira, adicionar pura e simplesmente o M2 ao modelo equivaleria a colocar o M1 duas vezes como variável. Para contornar este problema, foi subtraído o M1 do M2, para ficar apenas com a parte deste último que não está incorporada ao M1.
ouro: preço da onça de ouro em dólares americanos no London Bullion Market.
soja: preço da soja nos EUA.
trigo: preço do trigo nos EUA.
milho: preço do milho nos EUA.
O modelo econométrico escolhido para as estimações é o VAR, para a partir dele utilizar as análises de decomposição de variância e funções impulso-resposta no intuito de responder a questão proposta por este trabalho. Sua utilização se justifica tanto pela necessidade de verificar as interações das variáveis no tempo, como a de se analisar o impacto dinâmico de distúrbios aleatórios no sistema.
A primeira etapa no tratamento de séries temporais consiste em verificar se as variáveis utilizadas seguem um processo estocástico estacionário ou não. A Tabela 1 mostra o resultado do teste Augmented Dickey-Fuller sobre as variáveis selecionadas.
Tabela 1 - Testes de Raiz unitária - Augmented Dickey-Fuller (ADF)
|
||
Variável |
Estat. t |
Prob. |
ffr |
-3,252330 |
0,0755* |
m1 |
2,565249 |
1,0 |
m2lm1 |
0,933540 |
0,9999 |
ouro |
-1,375124 |
0,8673 |
soja |
-3,730593 |
0,0211** |
trigo |
-3,186559 |
0,0882 |
milho |
-2,985883 |
0,1371 |
D.ffr |
-5,895160 |
0,0*** |
D.m1 |
-4,824392 |
0,0005*** |
D.m2lm1 |
-9,868453 |
0,0*** |
D.ouro |
-16,54824 |
0,0*** |
D.trigo |
-15,67144 |
0,0*** |
D.milho |
-16,40598 |
0,0*** |
*,** e *** indicam significância aos níveis de 10, 5 e 1% respectivamente "D." indica primeira diferença Todos os testes foram realizados considerando tendência e constante das séries |
||
Como se pode observar apenas a variável soja se mostrou estacionária em nível, enquanto as demais apresentaram raiz unitária em nível e estacionariedade em primeira diferença. Desta maneira, lembrando que conforme apontam Johnston e DiNardo (1997, cap. 9), quando as variáveis do VAR são integradas estas ficam sujeitas a inconsistências. Assim sendo, a estimação do modelo será realizada apenas considerando variáveis estacionárias. Assim sendo, o segue a seguinte especificação:
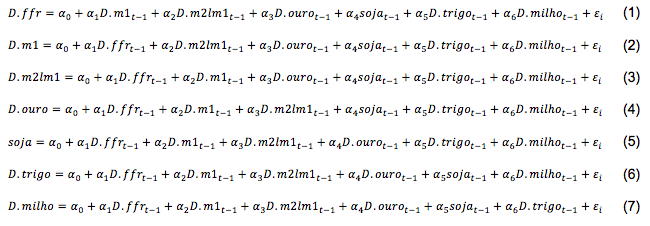
O próximo passo a se seguir após a aplicação dos testes de raiz unitária é a seleção do número de defasagens a serem utilizadas. Para isto, adotamos o procedimento de redução do número de defasagens do modelo proposto, tomando como referência os resultados dos testes apresentados na Tabela 2.
A Tabela 2 mostra que dos cinco critérios utilizados, apenas o LR indicou oito defasagens, portanto, esse resultado foi desconsiderado. Nos quatro testes restantes, dois deles, o SC e HQ, indicaram a utilização de uma defasagem, enquanto que o FPE e AIC indicaram quatro defasagens. Mediante este empate, optou-se pelo modelo com quatro defasagens para evitar o problema de autocorrelação que pode aparecer em modelos com poucas defasagens.
Tabela 2 – Teste de Seleção de Defasagens do Modelo VAR
Lag |
LogL |
LR |
FPE |
AIC |
SC |
HQ |
0 |
-6150.094 |
NA |
59724.02 |
30.86263 |
30.93261 |
30.89035 |
1 |
-5086.488 |
2084.562 |
369.3629 |
25.77688 |
26.33674* |
25.99861* |
2 |
-4999.660 |
167.1282 |
305.6298 |
25.58727 |
26.63699 |
26.00301 |
3 |
-4943.813 |
105.5337 |
295.4778 |
25.55295 |
27.09255 |
26.16271 |
4 |
-4887.887 |
103.7224 |
285.6853* |
25.51823* |
27.54770 |
26.32201 |
5 |
-4851.015 |
67.09192 |
304.0906 |
25.57902 |
28.09836 |
26.57681 |
6 |
-4802.726 |
86.16830 |
305.9224 |
25.58259 |
28.59181 |
26.77440 |
7 |
-4763.939 |
67.85445 |
323.0829 |
25.63378 |
29.13287 |
27.01960 |
8 |
-4711.547 |
89.81345* |
319.0712 |
25.61678 |
29.60574 |
27.19662 |
* Indica o número de defasagens selecionadas pelo critério. LR: sequential modified LR test statistic (each test at 5% level) FPE: Final prediction error AIC: Akaike information criterion SC: Schwarz information criterion HQ: Hannan-Quinn information criterion |
||||||
A Figura 1 sistematiza graficamente os resultados da análise de decomposição de variância para as quatro commodities estudadas neste trabalho[5]. Os resultados mostram que as variáveis de monetárias ffr, m1 e m2lm1 têm um impacto muito maior sobre a variância do ouro do que das demais commodities. Respectivamente, ffr, m1 e m2lm1 apresentam um impacto de 1,50%, 9,90% e 5,76% sobre a variância do ouro. Para a soja, trigo e milho, o maior valor observado que as variáveis monetárias exercem sobre elas é de 3,35%, que se refere à influência do m2lm1 sobre o trigo, sendo que em vários outros casos, observam-se valores inferiores a 1%.
Figura 1 - Decomposição de variância

Para as commodities agrícolas analisadas, o comportamento que se observa é que elas exercem grandes influências sobre a variância umas das outras. Por exemplo, 9,20% da variância da soja é explicada pela do trigo, enquanto que 8,87% da variância do trigo é relacionada à soja. Entretanto o resultado mais emblemático é o do milho, em relação ao qual 13,38% da variância é explicada pela do trigo e 30,58% pela da soja.
As funções impulso-respostas apresentadas nesta seção foram geradas a partir de um modelo VAR, similar ao utilizado para a análise de decomposição de variância, exceto pelo fato de que neste caso utilizamos todas as variáveis em nível e nenhuma em primeira diferença. A escolha pela utilização desta especificação do VAR nesta seção se deve ao nosso entendimento de que as funções impulso-resposta com as variáveis em nível proporcionam um melhor entendimento da interação das variáveis no tempo.
Como mostra Phillips (1998), é possível calcular funções impulso-resposta para modelos VAR que apresentem raízes unitárias, contanto que não se trabalhe com longos horizontes de tempo.
Our asymptotic analysis shows that in non-stationary VAR models with some roots at or near unity the estimated impulse response matrices are inconsistent at long horizons and tend to random matrices rather than the true impulse responses. (Phillips, 1998, p.45).
Desta maneira, as funções impulso-resposta desta seção foram calculadas utilizando apenas um horizonte de tempo de dez períodos à frente, para se evitar esses problemas de inconsistência.
A análise dos gráficos de impulso-resposta representados na Figura 2 corroboram com os resultados verificados anteriormente nas análises de decomposição de variância. Novamente as variáveis monetárias ffr, m1 e m2lm1 apresentam um maior impacto sobre o ouro, sendo que, além disso, elas mostram efeitos claros que não se observam nas outras commodities.
Choques no ffr geram uma resposta negativa no preço do ouro, enquanto que em relação ao m1 e m2lm1 o comportamento é o oposto. Para todas as variáveis analisadas, a resposta do ouro é bem clara, e indicam que ele se mostra como uma opção factível para agentes que queiram se proteger de afrouxamentos monetários relativos ao dólar.
Para a soja, trigo e milho, a resposta das variáveis monetárias não é tão clara conforme a observada para o ouro. Por exemplo, o ffr para essas três commodities apresenta uma resposta nos primeiros períodos, que se altera de sinal nos períodos seguintes. Para a soja e o milho a resposta é inicialmente positiva e posteriormente se torna negativa, sendo que com o trigo observa-se o comportamento inverso. Para os agregados monetários m1 e m2lm1, apenas o trigo apresenta uma resposta estritamente positiva. A soja inicialmente responde de forma positiva, posteriormente entra em terreno negativo e volta a subir. Por fim, a reposta do milho para o m1 é similar ao que se observa com a soja, sendo que a resposta ao m2lm1 é semelhante à observada com o trigo.
Figura 2 - Gráficos das funções impulso-resposta

Historicamente as commodities agrícolas são um tema de grande importância dentro das ciências sociais, tanto por suas implicações econômicas como políticas. Isto atrelado a fortes movimentos de alta registrados nos últimos anos da primeira década do século XXI gerou muitos debates a respeito dos determinantes de seus preços. Alguns autores, como Masters (2008 e 2009), culpam a especulação financeira por uma sobrevalorização desses produtos, que entre outras coisas causou o aumento da fome e da pobreza pelo mundo. Já outros estudos, munidos de dados e modelos estatísticos, mostram evidências de que o preço dessas commodities é guiado prioritariamente por seus fundamentos.
Dentre as commodities agrícolas, este artigo buscou analisar especificamente o comportamento da soja, trigo e milho, frente à política monetária dos EUA. Desta forma, como método de análise, optou-se pela utilização de um modelo VAR e suas ferramentas de decomposição de variância e funções impulso-resposta.
O modelo proposto incluiu como variáveis as três commodities foco deste estudo, a taxa de juros e os agregados monetários M1 e M2 dos EUA, mais o ouro. A inclusão do ouro no modelo deu-se pelo fato de existir vasta literatura que o aponta como uma defesa natural do mercado contra políticas de afrouxamento monetário. Nesse sentido, ele serve de comparativo para verificar se as outras commodities também apresentam esse comportamento defensivo ou não.
Os resultados verificados mostram que as commodities agrícolas analisadas sofrem influências muito mais limitadas das variáveis monetárias do que o ouro. Por exemplo, a análise de decomposição de variância da soja e do trigo mostra que menos de 1% da variância deles é explicada pela taxa de juros americana. Já as funções impulso-resposta não apresentam um comportamento claro de como essas commodities se comportam frente à política monetária. Todos estes comportamentos distintos do observado com o ouro. Este apresentou parcelas maiores de sua variância explicada pelas variáveis monetárias e nas funções impulso-resposta exibiu um comportamento claramente positivo em resposta aos agregados monetários e negativo frente à taxa de juros.
As commodities agrícolas apresentaram como principais responsáveis por suas variações de preços o comportamento de seus congêneres. Mais especificamente, 9,20% da variância da soja é explicada pelo trigo, 8,87% da variância do trigo é relacionada à soja, e por fim, 30,58% da variância do milho é oriunda da soja. Estes resultados, em especial o do milho, que é o que chama mais a atenção, pode indicar algum grau de complementariedade e substituibilidade entre essas commodities, o que do ponto de vista teórico justificaria o peso elevado que umas têm sobre o comportamento das outras.
Pelos resultados verificados ao longo do artigo, nota-se que existem indícios de que a dinâmica de preços das commodities agrícolas analisadas se deve muito mais aos fundamentos de seus mercados do que a movimentos especulativos relacionados à política monetária. Também não se verificou nenhum indicativo, do ponto de vista especulativo, de que alguma dessas commodities pudesse ser mais interessante que o ouro em um movimento contra um afrouxamento do dólar.
Desta forma, longe de querer esgotar a discussão sobre o tema, até porque apenas três de inúmeras commodities agrícolas foram analisadas, conclui-se que os resultados apresentados mostram indícios de que movimentos especulativos contra o enfraquecimento do dólar não contribuem decisivamente para o aumento de preços das commodities agrícolas. Portanto, do ponto de vista empírico, não encontramos sustentação para o argumento de que a especulação faz as pessoas passarem fome.
AREZKI, R.; M. BRUCKNER. Food Prices and Political Instability. Working paper, International Monetary Fund, 2011.
BARSKY, R. B.; SUMMERS, L. H. Gibson's Paradox and the Gold Standard. NBER WORKING PAPER SERIES, n. 1680, 1985.
BORDO, M. D.; WHEELOCK, D. C. Monetary Policy And Asset Prices: A Look Back At Past U.S. Stock Market Booms. NBER Working Paper Series, n. 10704, 2004.
COOPER, R. N.; LAWRENCE, R. Z. The 1972-75 commodity boom. Brookings Papers on Economic Activity, n. 3, 1975.
ETIENNE, X. L.; IRWIN, S. H.; GARCIA, P. Price Explosiveness, Speculation, and Grain Futures Prices. American Journal of Agricultural Economics, 2014, p. 01-23.
FAWLEY, B.; JUVENAL, J. Commodity Price Gains: Speculation vs. Fundamentals. The Regional Economist, vol. 19, n. 3, 2001.
FRANKEL, J. A. The Effect of Monetary Policy on Real Commodity Prices. Asset Prices and Monetary Policy, Chicago, The University of Chicago Press, p. 291-333, 2008.
JOHNSTON, J.; DINARDO, J. Econometric Methods. 4 ed. Singapore, McGraw-Hill. 1997.
LÜTKEPOHL, H. New Introduction to Multiple Time Series Analysis. Berlin, Springer-Verlag, 2005.
MASTERS, M. W. Testimony before the Committee on Homeland Security and Governmental Afairs. 2008, Disponível em: <www.hsgac.senate.gov/ public/ _files/052008Masters.pdf> Acesso em: 5. Jan. 2015.
MASTERS, M. W. Testimony before the Commodities Futures Trading Commission. 2009, Disponível em: <http://www.cftc.gov/ucm/groups/public/ @newsroom/documents/file/hearing080509_masters.pdf.> Acesso em: 5. Jan. 2015.
MITCHELL, D. A Note on Rising Food Prices. The World Bank Development Prospects Group, Policy Research Working Paper 4682, 2008.
NATANELOV, V. et al. Is there co-movement of agricultural commodities futures prices and crude oil? Energy Policy, n. 39, p. 4971-4984, 2011.
PAUL, J. A.; WAHLBERG, K. A. New Era of World Hunger? The Global FoodCrisis Analyzed. FES Briefing Paper, Julho, 2008.
PHILLIPS, P. C. B. Impulse response and forecast error variance asymptotics in nonstationary VARs. .Journal of Econometrics, n. 83, p. 21-56, 1998.
WHITE, W. R. Ultra Easy Monetary Policy and the Law of Unintended Consequences. Federal Reserve Bank of Dallas, Working Paper n. 126, 2012.
WORLD BANK. Global Economic Prospects 2009: Commodities at the Crossroads. Washington, World Bank, 2008.
Decomposição de Variância de D.ouro: |
||||||||
Period |
S.E. |
D.ffr |
D.m1 |
D.m2lm1 |
D.ouro |
soja |
D.trigo |
D.milho |
1 |
0.330852 |
0.040182 |
4.756205 |
3.682177 |
91.52144 |
0.000000 |
0.000000 |
0.000000 |
2 |
0.368970 |
1.083044 |
8.338945 |
5.969875 |
82.61942 |
0.714356 |
0.397164 |
0.877196 |
3 |
0.372962 |
1.381114 |
8.356049 |
5.902690 |
81.70005 |
0.873437 |
0.406338 |
1.380317 |
4 |
0.375146 |
1.442061 |
9.550164 |
5.810559 |
80.48860 |
0.945153 |
0.401567 |
1.361895 |
5 |
0.375770 |
1.458791 |
9.556421 |
5.671919 |
78.47574 |
0.930344 |
1.476460 |
2.430326 |
6 |
0.376289 |
1.443327 |
9.590696 |
5.736673 |
77.63914 |
0.930956 |
2.188785 |
2.470424 |
7 |
0.376520 |
1.437119 |
9.836774 |
5.712367 |
77.35089 |
0.936441 |
2.238748 |
2.487665 |
8 |
0.376567 |
1.437939 |
9.888825 |
5.708946 |
77.28203 |
0.936042 |
2.249197 |
2.497022 |
9 |
0.376604 |
1.468790 |
9.908595 |
5.741807 |
77.07988 |
0.938567 |
2.368418 |
2.493946 |
10 |
0.376624 |
1.509324 |
9.896534 |
5.763949 |
76.97680 |
0.939121 |
2.382223 |
2.532051 |
Decomposição de Variância de soja: |
||||||||
Period |
S.E. |
D.ffr |
D.m1 |
D.m2lm1 |
D.ouro |
soja |
D.trigo |
D.milho |
1 |
11.63704 |
0.104408 |
0.393633 |
0.668496 |
1.665752 |
97.16771 |
0.000000 |
0.000000 |
2 |
11.88349 |
0.041355 |
1.031334 |
0.431172 |
1.280489 |
97.12792 |
0.071333 |
0.016400 |
3 |
12.01046 |
0.067183 |
1.532281 |
0.256969 |
1.174703 |
96.64049 |
0.291458 |
0.036915 |
4 |
12.38744 |
0.053133 |
1.683277 |
0.374960 |
0.860912 |
95.94849 |
1.048604 |
0.030621 |
5 |
12.41664 |
0.044564 |
1.896187 |
0.692308 |
0.660290 |
93.24701 |
3.320954 |
0.138686 |
6 |
12.48068 |
0.061274 |
2.095657 |
1.041915 |
0.607701 |
89.90846 |
5.945583 |
0.339408 |
7 |
12.56018 |
0.069492 |
2.291716 |
1.360289 |
0.691739 |
87.32277 |
7.683324 |
0.580669 |
8 |
12.59327 |
0.062100 |
2.384888 |
1.627360 |
0.781442 |
85.78642 |
8.528776 |
0.829016 |
9 |
12.64041 |
0.056876 |
2.372182 |
1.812635 |
0.820850 |
84.91703 |
8.932321 |
1.088104 |
10 |
12.69368 |
0.064671 |
2.320056 |
1.934695 |
0.825271 |
84.31920 |
9.205529 |
1.330576 |
Decomposição de Variância de D.trigo: |
||||||||
Period |
S.E. |
D.ffr |
D.m1 |
D.m2lm1 |
D.ouro |
soja |
D.trigo |
D.milho |
1 |
20.69555 |
0.026575 |
1.407076 |
1.737234 |
0.236702 |
9.811955 |
86.78046 |
0.000000 |
2 |
21.92667 |
0.221438 |
1.658341 |
3.356037 |
2.763887 |
8.797400 |
83.20235 |
0.000549 |
3 |
22.45290 |
0.232365 |
1.655160 |
3.382885 |
3.587155 |
8.717623 |
82.42421 |
0.000606 |
4 |
23.30507 |
0.284984 |
1.633701 |
3.271288 |
4.097225 |
8.622781 |
81.63380 |
0.456220 |
5 |
23.68010 |
0.559879 |
1.705107 |
3.237600 |
4.089719 |
8.697884 |
80.50432 |
1.205490 |
6 |
23.95781 |
0.758502 |
1.831182 |
3.276302 |
4.054400 |
8.754125 |
79.99810 |
1.327388 |
7 |
24.16169 |
0.837877 |
1.822562 |
3.264678 |
4.052063 |
8.741046 |
79.91130 |
1.370475 |
8 |
24.32403 |
0.844264 |
1.855833 |
3.260079 |
4.046399 |
8.790753 |
79.82784 |
1.374828 |
9 |
24.49007 |
0.845098 |
1.891337 |
3.255834 |
4.041257 |
8.838468 |
79.73841 |
1.389596 |
10 |
24.68756 |
0.853010 |
1.892463 |
3.255135 |
4.037540 |
8.874063 |
79.68091 |
1.406883 |
Decomposição de Variância de D.milho: |
||||||||
Period |
S.E. |
D.ffr |
D.m1 |
D.m2lm1 |
D.ouro |
soja |
D.trigo |
D.milho |
1 |
26.18604 |
0.507448 |
0.457998 |
0.942387 |
0.489641 |
35.87142 |
3.817509 |
57.91360 |
2 |
27.81272 |
0.458882 |
0.808192 |
2.271961 |
0.855868 |
35.61542 |
5.871517 |
54.11816 |
3 |
27.98297 |
0.441725 |
1.284855 |
2.536861 |
0.893558 |
34.32551 |
8.056815 |
52.46068 |
4 |
28.26734 |
0.605590 |
1.727366 |
2.464286 |
2.281418 |
33.18663 |
8.647085 |
51.08762 |
5 |
28.63770 |
0.845590 |
1.800992 |
2.473219 |
4.823644 |
30.58825 |
12.31615 |
47.15215 |
6 |
28.82737 |
0.944261 |
1.798367 |
2.493058 |
5.559618 |
29.99366 |
13.41986 |
45.79117 |
7 |
28.90770 |
0.951664 |
1.880108 |
2.481426 |
5.842607 |
29.83458 |
13.41903 |
45.59059 |
8 |
28.92246 |
1.057914 |
1.880069 |
2.489709 |
5.887490 |
29.72553 |
13.44292 |
45.51638 |
9 |
28.96143 |
1.168203 |
1.969488 |
2.515047 |
5.866880 |
29.59705 |
13.39465 |
45.48868 |
10 |
28.98181 |
1.220532 |
1.986659 |
2.547325 |
5.854820 |
29.54585 |
13.38171 |
45.46311 |
Ordenação de Cholesky: D.ffr ; D.m1 ; D.m2lm1 ; D.ouro ; soja ; D.trigo ; D.milho
1. Doutorando em Teoria Econômica pela Universidade Estadual de Maringá, UEM. Mestre em Desenvolvimento Econômico pela Universidade Federal do Paraná, UFPR.
2. Professor Associado do Departamento de Economia da Universidade Estadual de Maringá, UEM. E-mail: afalves@gmail.com
3. Professor Titular do Departamento de Economia da Universidade Estadual de Maringá, UEM. E-mail: jlparre@gmail.com
4. Há, evidentemente, commodities de elevada importância tanto em termos de consumo, como geração de emprego e renda no mundo. Um exemplo é o arroz. No entanto, optou-se por utilizar dados das três mais representativas em termos de participação em mercados de derivativos, notadamente o norte americano. Além disso, as três commodities escolhidas têm fortes ligações com a questão da segurança alimentar, tanto direta quanto indiretamente, em função de seu uso como componente de rações animais.
5. A tabela com os resultados numéricos das decomposições de variância encontra-se no Apêndice 1.