

Vol. 38 (Nº 57) Year 2017. Page 8
John Edwin CANDELO Becerra 1; Helman Enrique HERNÁNDEZ Riaño 2; Alcides Ricardo SANTANDER Mercado 3
Received: 16/07/2017 • Approved: 15/08/2017
ABSTRACT: The use of distributed generation (DG) is an important strategy of electricity companies to improve the power losses in distribution networks. This paper proposes a hybrid algorithm based on the bat-inspired algorithm (BA) and the harmony search algorithm (HS) to avoid premature convergence. The results showed that the new hybrid algorithm has the advantage of converging quickly to the best solutions and finds better solutions through a combination of the best positions of individuals. |
RESUMEN: El uso de Generación Distribuida (GD) es una importante estrategia de las compañías eléctricas para mejorar las pérdidas de potencia en sus redes de distribución. Este artículo propone un algoritmo híbrido basado en el algoritmo inspirado en murciélagos y en el algoritmo de búsqueda armónica que evita la convergencia prematura. Los resultados obtenidos muestran que el nuevo algoritmo tiene como ventajas que converge rápidamente hacia las mejores soluciones y que encuentra soluciones de buena calidad. |
Power losses represent a major problem for the energy efficiency of distribution networks and distribution system operators (DSOs) must deal with the improvement to avoid higher operating cost. A reduction in the power losses in a distribution network is beneficial to improve power transfer, voltage magnitudes, power quality, and voltage stability.
DSOs have several alternatives for facing the energy losses. Some of the best options include the use of DG (Atwa, El-Saadany, Salama, & Seethapathy, 2010; Hung, Mithulananthan, & Bansal, 2010, 2013; Naik, Khatod, & Sharma, 2012; Singh & Parida, 2011; D. D. Wu, Junjie, Yulong, & Yang, 2012; Zhang, Fu, & Zhang, 2008), capacitor placement (Ramesh & Chowdhury, 2009; Singh & Parida, 2011), feeder restructuring (Ramesh & Chowdhury, 2009), and network reconfiguration (R. S. Rao, Ravindra, Satish, & Narasimham, 2013; Y.-K. Wu, Lee, Liu, & Tsai, 2010). DG is widely used because of the amount of energy supplied close to the loads, which allows improvement of the operating conditions of the network. DG can be financed by the DSO, the investor, or the final users, and the decision must be supported by the electricity-market regulation in each country.
The development of the DG in many countries allows final users to install sources, but doing so decreases the requested load in the network and is normally conceived for economics’ sake. However, this method is not focused on improving the electrical network and its operation, since the load reduction is performed at some points of the network with no optimization process. Thus, it is preferable that electricity companies select the best points to install the new generators, supporting better use of the energy resources.
The implementation of DG by the DSO or the investors is a good option to maintain better conditions in the network. The experimental results of the method have shown that it is useful for the network; therefore, it should be prioritized for the development of power grids and to obtain better reliability in the electricity service. For that reason, this research proposes an algorithm that finds the best location for DG to develop the power grid by means of the DSO or the investors. For some countries, implementing the solution must lead to some changes in the regulation of the electricity market, especially the roles of the participants.
The installation of the DG in the distribution network benefits participants in the electricity market. The DSO has more availability in the network, less congestion, greater reliability, better power quality, etc. Generation investors would be able to participate in the production of electricity closer to the users. The retailer would have more options for purchasing electricity, which means lower prices and achieving greater competitiveness in the market. Users will have options for reducing the costs of electricity, and they also can coordinate with the DSO, investors, and retailers to install DG and improve the availability of electricity.
Determining the best location and size of DG using exact techniques can be a time-consuming computation. Metaheuristic algorithms are generally robust techniques that provide near-optimal solutions for this type of problem (Georgilakis & Hatziargyriou, 2013). Several metaheuristics have been tested to solve this problem (Tan, Hassan, Majid, & Abdul Rahman, 2013), such as the particle swarm optimization (PSO) (El-Zonkoly, 2011; Kansal, Sai, Tyagi, & Kumar, 2011; Lalitha, Reddy, & Usha, 2010; Mohammad & Nasab, 2011), ant colony (AC) (Sookananta, Utaton, & Khongsila, 2010; L. Wang & Singh, 2008), evolutionary algorithm (EA) (Borges & Falcão, 2006; Celli, Ghiani, Mocci, & Pilo, 2005; Shaaban, Atwa, & El-Saadany, 2012), simulated annealing (SA) (Aly, Hegazy, & Alsharkawy, 2010; Ghadimi & Ghadimi, 2012), and BA (Candelo Becerra & Hernández Riaño, 2015), HS (Parizad, Khazali, & Kalantar, 2010; K. S. Rao & Rao, 2012). These algorithms do not guarantee an optimal solution for the problem studied. Therefore, researchers are continually searching for the best algorithms to solve each problem.
One of the most important algorithms recently tested to solve this problem was the BA, obtaining good results when locating and sizing the DG, but several convergence problems have been detected when trying to solve difficult problems (Candelo Becerra & Hernández Riaño, 2015). The advantage of this technique is the fast movements of the individuals to the best location, but a search of the best solutions can be limited according to the solutions found near the optimum, requiring the testing of other combinations to avoid convergence problems.
Another important algorithm is the HS, with the capacity to generate a new solution vector after considering all vectors previously obtained as solutions. The algorithm combines good solutions found during different iterations, increasing the flexibility and capacity to obtain better solutions (Mahdavi, Fesanghary, & Damangir, 2007).
Therefore, this research proposed a new BA with HS for searching the best solutions to find the location and size of the DG and for improving the search of different cases. The combinations of these techniques are reported as good results for numerical problems (G. Wang & Guo, 2013), but their effectiveness in applications for electrical engineering and the implementation of better techniques according to the problem are needed.
The development of hybrid metaheuristic algorithms is an important issue for determining the best location and size of DG. For that reason, some researchers have focused on developing new techniques to improve the search (Evangelopoulos & Georgilakis, 2014; Kollu, Rao Rayapudi, & Narasimham Sadhu, 2014; Yammani, Maheswarapu, & Kumari Matam, 2015).
The model presented in this research seeks to represent the problem of power losses in distribution networks from the point of view of the electricity companies, where DG is used to reduce power losses (Manafi, Ghadimi, Ojaroudi, & Farhadi, 2013).



The BA and HS techniques have exhibited a good performance in different engineering problems. However, for the location and size of the DG, the algorithms have shown difficulties in finding better solutions, especially for several generators. Therefore, we propose the use of the CBAHS to determine better solutions in a reduced number of iterations.
For the implementation of the algorithms, the problem was encoded as shown in Figure 1. This codification represents the location and size of distributed generators. Each individual or particle inside the algorithm corresponds to a solution of the problem.
Where x, y and z represent the real power supplied, the reactive power supplied, and the number of node where the generator is located, respectively. nd is the number of generators.
Figure 1
Problem codification for location and size of distributed generators.

This algorithm was first presented by (Yang, 2010), and it is based on the echolocation of bats during the search for a prey. The algorithm starts with an initial population and moves all bats using the frequency and velocity. The use of random flies helps in finding new solutions in the searching region. The steps implemented in this work were programmed in the Matlab software as follows:

This algorithm was first proposed by (Zong Woo Geem, Joong Hoon Kim, & Loganathan, 2001) in 2001, and it is based on the improvisation made by musicians when playing instruments. The steps of the algorithm are described as follows:

The hybridization of the algorithms is conducted to improve the search of the objective function by flying randomly using a harmony search combination. The steps implemented in the algorithm were based on (G. Wang & Guo, 2013).

The hybridization of these algorithms is conducted to improve the convergence towards solutions when the combinatorial problems become more difficult. The best characteristics of the BA and HS were combined to improve the search for a fast combinatorial solution. BA conducts the main search to take advantage of its high speed of convergence, and HS is activated only when the search has been trapped in a local optimum. Reactivation of the initial algorithm BA is conducted when a new good solution is found using the HS and the cycle repeat until the last iteration. This combination of algorithms was performed to obtain a fast hybrid algorithm with the possibility to escape from local optimal solutions when solving the problem of locating and sizing distributed generation.
The steps implemented in the algorithm are described as follows:

To test the proposed metaheuristic, two balanced distribution network were used. The 33-node and 69-node radial distribution networks are standard cases used to test the location and size of the DG.
This distribution network has 33 nodes with one feeder at node 1 and 32 loads for the rest of the system (Baran & Wu, 1989; Taher & Afsari, 2012). Figure 2 shows the diagram of the 33-node radial distribution network.
Figure 2
Case 33-node radial distribution network. Source:(Taher & Afsari, 2012).
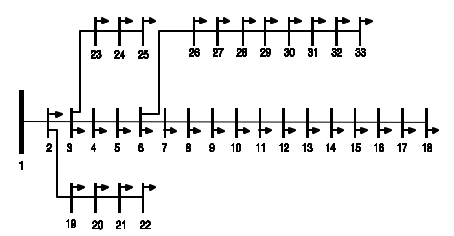
Case 33-node radial distribution network has a total load of 3715 kW and 2300 kVAr and a total supply of 3926 kW and 2443 kVAr. The voltage limits at the load buses were defined as Vmin=0.9 p.u. and Vmax=1.1 p.u. The possible nodes to locate the DG were selected according to the definition of the PQ nodes, providing a total of 32 nodes.
This distribution network has 69 nodes with one feeder at node 1 and 49 loads as shown in Figure 3 (Phonrattanasak & Leeprechanon, 2012; Taher & Afsari, 2012). This distribution network has a total load of 4014 kW and 2845 kVAr and a total generation 4265 KW and 2957 kVAr. The voltage limits at the load buses were considered as 10% of the rated voltage or Vmin=0.9 p.u. and Vmax=1.1 p.u. The possible nodes for locating the DG were selected according to the definition of the PQ nodes, providing a total of 68 nodes.
Figure 3
Case 69-node radial distribution network. Source:(Taher & Afsari, 2012).
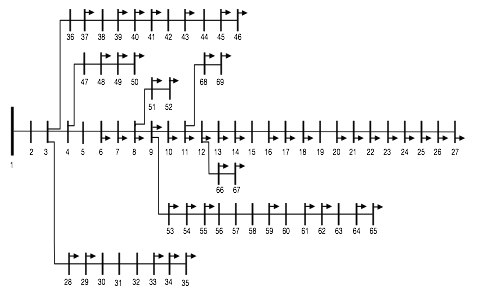
The simulation scenarios presented in this study aimed to evaluate the performance of the proposed algorithm. Variations in the number and size of DG were performed to find the best location in the distribution network to supply electricity to the different levels of demand. The selection of the power system cases, the design of the simulations scenarios, and the determination of the parameters of operation, including in the algorithms, were carried out as described in the literature and in previous works published by the authors of the present study.
Previous research has determined that the location and size of a few generators and lower capacities are not a problem for metaheuristics with a small number of individuals and iterations (Candelo Becerra & Hernández Riaño, 2015). Because a large number of generators and capacities showed different results, this paper focuses on the search for better results with a hybrid BA-HS with generators changing from five to seven for the 33-node and 69-node radial distribution networks. The maximum power tested in (Candelo Becerra & Hernández Riaño, 2015) was used to compare all of the algorithms and to determine the best solutions. The power selected for each generator has a maximum real power of 2 MW with a power factor of 0.98 inductive.
The test consisted of obtaining similar characteristics for the four algorithms to evaluate the performance of each technique and determine the advantages. Comparisons of the minimum objective functions and the average of solutions were performed, considering the following parameters:
Table 1 shows the results of the location and size of the DG using the four algorithms for the 33-node and 69-node radial distribution networks, respectively. The column Case corresponds to the power system test, ng is the number of generators, Alg is the algorithm used to determine the solution for each scenario, Ptot is the total active power supplied by the generators, Nodes is the node numbers that represent the solution with the minimum Fitness, Fmin is the minimum fitness, Pfmin is the ranking of the solution according to the minimum fitness, Favg is the average of the five solutions, and Pfavg is the ranking of the solution according to the minimum average.
Table 1
Location and size of the DG
Case |
ng |
Alg |
Ptot |
Nodes |
Fmin |
Pfmin |
Favg |
Pfavg |
33-node case base |
0 |
- |
- |
- |
210,9 |
- |
- |
- |
33-node |
5 |
BA |
3573 |
10-30-24-6-16 |
35,98 |
4 |
36,39 |
3 |
HS |
3425 |
24-31-10-14-6 |
35,89 |
3 |
37,17 |
4 |
||
SBAHS |
3453 |
11-24-6-31-16 |
35,57 |
2 |
35,75 |
2 |
||
CBAHS |
3423 |
14-30-24-7-32 |
35,48 |
1 |
35,65 |
1 |
||
6 |
BA |
3440 |
24-15-11-7-32-30 |
34,41 |
3 |
35,13 |
3 |
|
HS |
3054 |
12-7-30-14-25-31 |
35,87 |
4 |
36,58 |
4 |
||
SBAHS |
3396 |
14-33-6-8-30-24 |
34,56 |
2 |
34,79 |
2 |
||
CBAHS |
3299 |
10-32-16-7-25-30 |
34,42 |
1 |
34,74 |
1 |
||
7 |
BA |
3349 |
10-29-9-31-25-7-15 |
34,81 |
3 |
35,20 |
3 |
|
HS |
3771 |
7-23-10-14-33-25-30 |
35,59 |
4 |
36,29 |
4 |
||
SBAHS |
3720 |
16-10-6-21-29-24-31 |
33,37 |
2 |
33,92 |
2 |
||
CBAHS |
3756 |
30-6-24-16-20-10-32 |
33,25 |
1 |
33,54 |
1 |
||
69-node case base |
0 |
- |
- |
- |
265,0 |
- |
- |
- |
69-node |
5 |
BA |
3747 |
61-54-18-21-50 |
38,78 |
4 |
40,28 |
4 |
HS |
4120 |
49-23-12-61-8 |
37,34 |
3 |
37,64 |
2 |
||
SBAHS |
3810 |
25-61-11-17-50 |
37,18 |
2 |
37,90 |
3 |
||
CBAHS |
3925 |
61-23-11-64-50 |
36,99 |
1 |
37,19 |
1 |
||
6 |
BA |
6066 |
64-61-51-4-49-21 |
38,34 |
4 |
39,61 |
4 |
|
HS |
4591 |
8-5-50-12-23-61 |
37,52 |
3 |
39,06 |
3 |
||
SBAHS |
3886 |
68-61-17-23-50-25 |
37,35 |
2 |
38,09 |
2 |
||
CBAHS |
3874 |
64-26-61-11-50-23 |
36,62 |
1 |
37,37 |
1 |
||
7 |
BA |
3376 |
61-64-16-11-21-38-63 |
38,81 |
4 |
38,96 |
3 |
|
HS |
3403 |
21-3-24-67-49-13-61 |
39,31 |
3 |
40,32 |
4 |
||
SBAHS |
4342 |
60-61-17-10-26-49-65 |
37,33 |
1 |
38,20 |
2 |
||
CBAHS |
3757 |
16-61-22-10-35-49-64 |
37,43 |
2 |
37,54 |
1 |
Favg was considered a good indicator to measure the quality of the solutions, being the lower value the best solution found. Considering this indicator, the BA and HS algorithms obtained the worse solutions in 83% of the scenarios evaluated, demonstrating limitations in the solution for the problem studied. The BA found good solutions for problems with a small number of possible combinations as the 33-node radial distribution network and the HS found good results for difficult problems.
The hybrids SBAHS and CBAHS had better results for most cases compared to the solutions found with single algorithms. The SBAHS algorithm obtained good solutions in 83% of the scenarios evaluated, what represents a good performance for the problem studied. On the other hand, the CBAHS algorithm obtained the best solutions in 100% of the scenarios evaluated, considering different number and size of generators. The CBAHS obtained the minimum value of all repetitions and the best average of solutions, and we can conclude that it is the best method tested for finding the location and size of the DG.
On the other side, the location of DG in the 33-node radial distribution network impacted positively the energy efficiency of the network for all cases studied, obtaining an average reduction of 175.9 KW or 83.4% with respect to the base case. In the 69-node radial distribution network, the power losses reduced 227.2 KW or 85.7% with respect to the base case.
Figure 4 shows the convergence of the three algorithms for the problem of locating and sizing six generators for scenario number 4. As a control of the experimental conditions, all algorithms considered the same initial population to avoid advantages with better random values and to evaluate the performance of the solutions during the iterations.
Figure 4
Convergence of the algorithms.
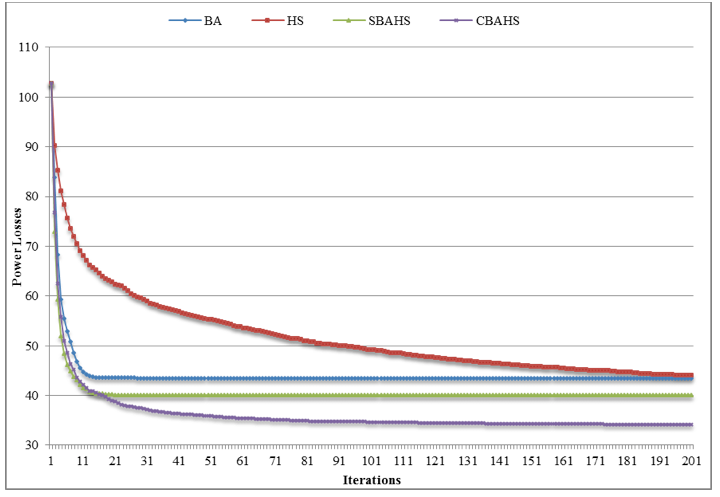
This figure shows that the BA is a method that rapidly found a good solution, reducing the fitness fast. As shown in the figure, the algorithm found a local solution and no improvement was seen during the other iterations.
The HS found solutions with a slow reduction in the average fitness. Because the method is based on the combination of different solutions, the results were better for difficult problems. After several iterations, the location provided better results compared with the solution offered with the BA. In conclusion, the HS is a good method for locating the DG, but the time for solving problems must be improved.
The proposed hybrid technique allowed the fast convergence offered by the BA and the search for better solutions with the HS. The figure show that the BA starts obtaining good and fast results and after moving close to the convergence, the search with HS is activated, allowing better solutions. If a new and good solution is found, the search with the BA is reactivated until the new criteria reactivate the HS. This search was tested up to the final iteration. Better results were not found after several iterations.
For the analysis of the convergence for the studied algorithms, it is important to note that CBAHS does not present problems of premature convergence for the BA because of the high diversity of the solutions provided by the HS in the moments that the algorithm requires it. This implies that the resulting algorithm has a high speed of convergence combined with a high diversity of solutions.
Figure 5 shows the voltage magnitudes of the 33-node radial distribution network for the base case and the location of 5 generators with the different algorithms.
Figure 5
Voltage magnitudes of the 33-node radial distribution network.
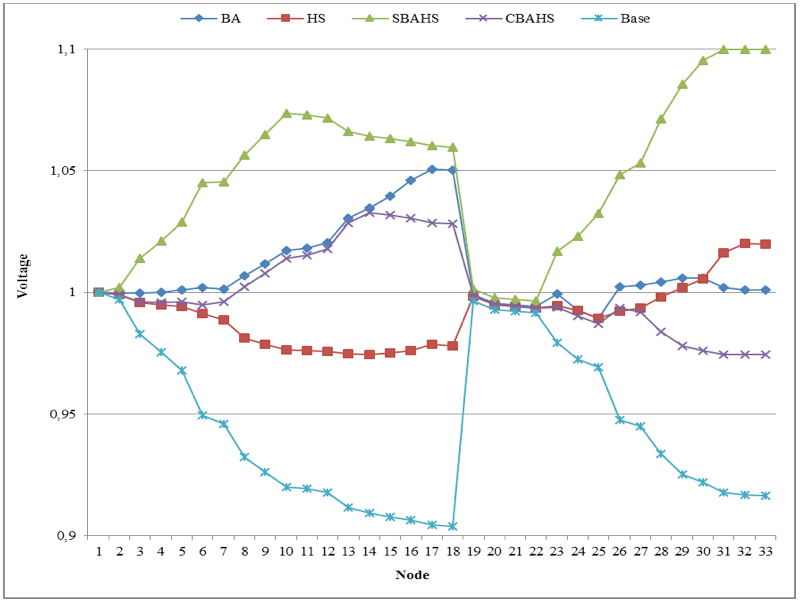
Application of metaheuristic algorithms for the location and size of distributed generation allowed an improvement of voltage magnitudes of the 33-node radial distribution network. The SBAHS algorithm obtained higher voltage magnitudes than the other algorithms, but some magnitudes are close to the maximum limits. The HS algorithm improved more the voltage magnitudes of nodes from 26 to 33 and less of nodes from 14 to 19. The BA improved more the voltage magnitudes of nodes from 14 to 19 and nodes from 26 to 33. Although these algorithms improve the voltages in different way, the reduction of power losses were not the best for the distribution network. Nevertheless, the CBAHS improved more the voltage magnitudes of nodes from 7 to 18 and less the voltage magnitudes of nodes from 28 to 33, representing the best compensation of power from distribution network to reduce power losses.
Figure 6 shows the voltage profiles of the 69-node radial distribution network after using the 5 generators located for the scenario with the different algorithms.
Figure 6
Voltage magnitudes for the 69-node radial distribution network
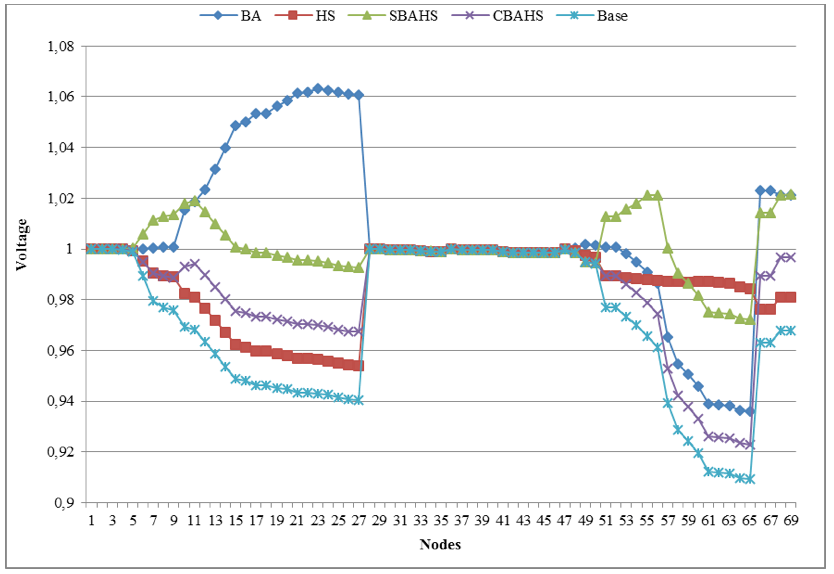
Metaheuristic algorithms allowed an improvement of voltage magnitudes of the 69-node radial distribution network, but the solutions obtained different magnitudes. The BA improved more the voltage magnitudes of nodes from 12 to 27 and the SBAHS improved more the voltage magnitudes of nodes from 51 to 58. The HS improved more the voltage magnitudes of nodes from 56 to 66 and less the voltage magnitudes of nodes from 12 to 27. Although the different improvement in voltage magnitudes with these algorithm, the reduction of power losses were not the best for the distribution network. Nevertheless, the hybrid CBAHS increased voltage magnitudes for all the nodes in a moderate way, maintaining a distributed compensation to reduce power losses from the base case and the effect of increasing new power losses with the distributed generation installed.
The BA, HS, hybrid SBAHS and CBAHS were implemented in this work to find the best location of the DG in two radial distribution networks. The results show that the BA needed a small number of iterations to obtain good results, while the HS needed a large number of iterations to obtain similar results. The HS algorithm is a slower method but has the advantage of evaluating a key number of combinations. The SBAHS had good results for most cases, improving the solutions with the use of the random flies HS. The proposed CBAHS method had better results especially when testing difficult cases, which allows a lower reduction in power losses compared with the other three methods. A comparison of the four methods showed that the hybrid methods improved the results with a smaller number of populations and iterations, which reduces the calculation time for solving difficult problems. The results presented in this research seek to provide new algorithms for electricity companies that find better solutions when locating distributed generation to improve power losses.
Aly, A. I., Hegazy, Y. G., & Alsharkawy, M. A. (2010). A simulated annealing algorithm for multi-objective distributed generation planning. In IEEE PES General Meeting (pp. 1–7). IEEE. http://doi.org/10.1109/PES.2010.5589950
Antmann, P. (2009). Reducing Technical and Non-Technical Losses in the Power Sector.
Atwa, Y. M., El-Saadany, E. F., Salama, M. M. A., & Seethapathy, R. (2010). Optimal Renewable Resources Mix for Distribution System Energy Loss Minimization. IEEE Transactions on Power Systems, 25(1), 360–370. http://doi.org/10.1109/TPWRS.2009.2030276
Baran, M. E., & Wu, F. F. (1989). Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Transactions on Power Delivery, 4(2), 1401–1407. http://doi.org/10.1109/61.25627
Borges, C. L. T., & Falcão, D. M. (2006). Optimal distributed generation allocation for reliability, losses, and voltage improvement. International Journal of Electrical Power & Energy Systems, 28(6), 413–420. Retrieved from http://www.sciencedirect.com/science/article/pii/S0142061506000482
Candelo Becerra, J. E., & Hernández Riaño, H. E. (2015). Distributed Generation Placement in Radial Distribution Networks using a Bat-inspired Algorithm. DYNA, 82(192), 60–67. http://doi.org/http://dx.doi.org/10.15446/dyna.v82n192.48573
Celli, G., Ghiani, E., Mocci, S., & Pilo, F. (2005). A Multiobjective Evolutionary Algorithm for the Sizing and Siting of Distributed Generation. IEEE Transactions on Power Systems, 20(2), 750–757. http://doi.org/10.1109/TPWRS.2005.846219
El-Zonkoly, A. M. (2011). Optimal placement of multi-distributed generation units including different load models using particle swarm optimization. Swarm and Evolutionary Computation, 1(1), 50–59. Retrieved from http://www.sciencedirect.com/science/article/pii/S2210650211000046
Evangelopoulos, V. a., & Georgilakis, P. S. (2014). Optimal distributed generation placement under uncertainties based on point estimate method embedded genetic algorithm. IET Generation, Transmission and Distribution, 8(3), 389–400. http://doi.org/10.1049/iet-gtd.2013.0442
Georgilakis, P. S., & Hatziargyriou, N. D. (2013). Optimal Distributed Generation Placement in Power Distribution Networks: Models, Methods, and Future Research. IEEE Transactions on Power Systems, 28(3), 3420–3428. http://doi.org/10.1109/TPWRS.2012.2237043
Ghadimi, N., & Ghadimi, R. (2012). Optimal Allocation of Distributed Generation and Capacitor Banks in Order to Loss Reduction in Reconfigured System. Research Journal of Applied Sciences, Engineering and Technology, 4(9), 1099–1104.
Hung, D. Q., Mithulananthan, N., & Bansal, R. C. (2010). Analytical Expressions for DG Allocation in Primary Distribution Networks. IEEE Transactions on Energy Conversion, 25(3), 814–820. http://doi.org/10.1109/TEC.2010.2044414
Hung, D. Q., Mithulananthan, N., & Bansal, R. C. (2013). Analytical strategies for renewable distributed generation integration considering energy loss minimization. Applied Energy, 105, 75–85. Retrieved from http://www.sciencedirect.com/science/article/pii/S0306261912009051
Kansal, S., Sai, B. B. R., Tyagi, B., & Kumar, V. (2011). Optimal placement of distributed generation in distribution networks. International Journal of Engineering, Science and Technology, 3(3), 47–55.
Kollu, R., Rao Rayapudi, S., & Narasimham Sadhu, V. L. (2014). A novel method for optimal placement of distributed generation in distribution systems using HSDO. INTERNATIONAL TRANSACTIONS ON ELECTRICAL ENERGY SYSTEMS, 24, 547–561. http://doi.org/10.1002/etep.1710
Lalitha, M. P., Reddy, V. C. V., & Usha, V. (2010). Optimal DG placement for minimum real power loss in radial distribution systems using PSO. Journal of Theoretical and Applied Information Technology, 13(2), 107–116.
Mahdavi, M., Fesanghary, M., & Damangir, E. (2007). An improved harmony search algorithm for solving optimization problems. Applied Mathematics and Computation, 188(2), 1567–1579. http://doi.org/10.1016/j.amc.2006.11.033
Manafi, H., Ghadimi, N., Ojaroudi, M., & Farhadi, P. (2013). Optimal Placement of Distributed Generations in Radial Distribution Systems Using Various PSO and DE Algorithms. ELEKTRONIKA IR ELEKTROTECHNIKA, 19(10), 53–57.
Mohammad, M., & Nasab, M. A. (2011). PSO Based Multiobjective Approach for Optimal Sizing and Placement of Distributed Generation. Research Journal of Applied Sciences, Engineering and Technology, 2(8), 823–837.
Naik, G., Khatod, D. K., & Sharma, M. P. (2012). Optimal Allocation of Distributed Generation in Distribution System for Loss Reduction. In International Proceedings of Computer Science and Information Technology IPCSIT.
Parizad, A., Khazali, A. H., & Kalantar, M. (2010). Sitting and sizing of distributed generation through Harmony Search Algorithm for improve voltage profile and reducuction of THD and losses. In CCECE 2010 (pp. 1–7). IEEE. http://doi.org/10.1109/CCECE.2010.5575177
Phonrattanasak, P., & Leeprechanon, N. (2012). Optimal Location of Fast Charging Station on Residential Distribution Grid - Volume 3 Number 6 (Dec. 2012) - IJIMT. International Journal of Innovation, Management and Technology, 3(6), 675–681.
Ramesh, L., & Chowdhury, S. (2009). Minimization of power Loss in distribution networks by different techniques. International Journal of Electrical and Electronics Engineering, 2, 521–527.
Rao, K. S., & Rao, M. N. (2012). Multiple distributed generator allocation by Harmony search algorithm for loss reduction. In 2012 International Conference on Emerging Trends in Electrical Engineering and Energy Management (ICETEEEM) (pp. 59–64). IEEE. http://doi.org/10.1109/ICETEEEM.2012.6494444
Rao, R. S., Ravindra, K., Satish, K., & Narasimham, S. V. L. (2013). Power Loss Minimization in Distribution System Using Network Reconfiguration in the Presence of Distributed Generation. IEEE Transactions on Power Systems, 28(1), 317–325. http://doi.org/10.1109/TPWRS.2012.2197227
Shaaban, M. F., Atwa, Y. M., & El-Saadany, E. F. (2012). DG Allocation for Benefit Maximization in Distribution Networks. IEEE Transactions on Power Systems, 28(2), 1–1. http://doi.org/10.1109/TPWRS.2012.2213309
Singh, A. K., & Parida, S. K. (2011). Selection of load buses for DG placement based on loss reduction and voltage improvement sensitivity. In 2011 International Conference on Power Engineering, Energy and Electrical Drives (pp. 1–6). IEEE. http://doi.org/10.1109/PowerEng.2011.6036559
Sookananta, B., Utaton, P., & Khongsila, R. (2010). Determination of the optimal location and sizing of Distributed Generation using Ant Colony Search. In 2010 International Conference on Electrical Engineering/Electronics Computer Telecommunications and Information Technology (ECTI-CON) (pp. 814–817). IEEE. Retrieved from http://ieeexplore.ieee.org/articleDetails.jsp?arnumber=5491597
Taher, S. A., & Afsari, S. A. (2012). Optimal location and sizing of UPQC in distribution networks using differential evolution algorithm. Mathematical Problems in Engineering, 2012. http://doi.org/10.1155/2012/838629
Tan, W.-S., Hassan, M. Y., Majid, M. S., & Abdul Rahman, H. (2013). Optimal distributed renewable generation planning: A review of different approaches. Renewable and Sustainable Energy Reviews, 18, 626–645. Retrieved from http://www.sciencedirect.com/science/article/pii/S1364032112005904
Wang, G., & Guo, L. (2013). A Novel Hybrid Bat Algorithm with Harmony Search for Global Numerical Optimization. Journal of Applied Mathematics, 2013, 1–21.
Wang, L., & Singh, C. (2008). Reliability-Constrained Optimum Placement of Reclosers and Distributed Generators in Distribution Networks Using an Ant Colony System Algorithm. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 38(6), 757–764. http://doi.org/10.1109/TSMCC.2008.2001573
Wu, D. D., Junjie, M., Yulong, W., & Yang, L. (2012). Size and Location of Distributed Generation in Distribution System Based on Immune Algorithm. Systems Engineering Procedia, 4, 124–132. Retrieved from http://www.sciencedirect.com/science/article/pii/S2211381911002104
Wu, Y.-K., Lee, C.-Y., Liu, L.-C., & Tsai, S.-H. (2010). Study of Reconfiguration for the Distribution System With Distributed Generators. IEEE Transactions on Power Delivery, 25(3), 1678–1685. http://doi.org/10.1109/TPWRD.2010.2046339
Yammani, C., Maheswarapu, S., & Kumari Matam, S. (2015). Optimal placement and sizing of distributed generations using shuffled bat algorithm with future load enhancement. INTERNATIONAL TRANSACTIONS ON ELECTRICAL ENERGY SYSTEMS. http://doi.org/10.1002/etep
Yang, X.-S. (2010). A New Metaheuristic Bat-Inspired Algorithm. In J. González, D. Pelta, C. Cruz, G. Terrazas, & N. Krasnogor (Eds.), Nature Inspired Cooperative Strategies for Optimization (NICSO 2010) SE - 6 (Vol. 284, pp. 65–74). Springer Berlin Heidelberg. http://doi.org/10.1007/978-3-642-12538-6_6
Zhang, D., Fu, Z., & Zhang, L. (2008). Joint Optimization for Power Loss Reduction in Distribution Systems. IEEE Transactions on Power Systems, 23(1), 161–169. http://doi.org/10.1109/TPWRS.2007.913300
Zong Woo Geem, Joong Hoon Kim, & Loganathan, G. V. (2001). A New Heuristic Optimization Algorithm: Harmony Search. SIMULATION. http://doi.org/10.1177/003754970107600201
1. Department of Electrical Energy and Automation, Universidad de Nacional de Colombia – Sede Medellín, Carrera 80 No. 65 – 223 Medellin - Colombia; E-Mail: jecandelob@unal.edu.co
2. Department of Industrial Engineering, Universidad de Córdoba, Carrera 6 No. 76-103 Montería - Colombia; E-Mail: hhernandez@correo.unicordoba.edu.co
3. Department of Industrial Engineering, Universidad del Norte, Km 5 Vía Puerto Colombia - Colombia; E-Mail: asantand@uninorte.edu.co