

Vol. 38 (Nº 18) Año 2017. Pág. 2
Douglas Joziel Bitencourt FREITAS 1; Paulo Sérgio SAUSEN 2; Airam Tereza Zago Romcy SAUSEN 3; Manuel Martín Pérez REIMBOLD 4
Recibido: 20/10/16 • Aprobado: 20/11/2016
3. Metodologia para Estimação de Parâmetros
4. Método dos Mínimos Quadrados
RESUMO: Neste artigo é apresentada a proposição de um modelo analítico, estendido a partir da Lei de Peukert, para predição do tempo de vida de baterias de LithiumIon Polymer (Li-Po), visan-do ampliar a acurácia do modelo original. O modelo foi avaliado através da comparação entre os resultados das simulações computacionais e os dados experimentais de uma bate-ria de Li-Po, sendo que para descargas com correntes constantes, o modelo obteve um erro médio de 1,07% e, para descargas com correntes variáveis, o erro médio foi de 2,41%. |
ABSTRACT: This paper presents the proposition of an analytical model, extended from the Peukert's Law to predict the lifetime of battery Lithiumion Polymer (Li-Po), to improve the accuracy of the original model. The model was evaluated by comparing the results of computer simulations and experimental data from a Li-Po, and to discharge with constant current, the model ob-tained an average error of 1.07% and, for discharges with current variables, the average error was 2.41%. |
A evolução tecnológica das últimas décadas provocou mudanças tanto nos ambientes e atividades do cotidiano, quanto na forma que as pessoas se relacionam com o mundo. A necessidade de estar conectado à rede de voz e dados, vem contribuindo para a rápida popularização do uso de dispositivos móveis – e.g., celulares, smartphones, tablets, notebooks, entre outros. Os dispositivos móveis agregam mobilidade, comodidade e facilidade de uso, contudo, têm o tempo de funcionamento limitado pela duração da fonte de energia, ou seja, pelo tempo de vida da bateria.
As baterias recarregáveis, utilizadas em dispositivos móveis, têm capacidade finita para o armazenamento de energia, necessitando após cada período de uso, de uma recarga. Deste modo, é importante dispor de métodos para predizer o tempo de vida de baterias e, consequentemente, o tempo de funcionamento dos dispositivos móveis. Uma das formas de realizar esta predição é através da modelagem matemática, utilizando modelos que podem descrever o comportamento dinâmico da descarga de baterias, a partir de suas características físicas reais ou, até mesmo, de um conjunto reduzido de dados experimentais.
Nos últimos anos, vários modelos matemáticos que descrevem a descarga de baterias – por conseguinte, seu tempo de vida – vêm sendo desenvolvidos e aprimorados, dos quais destacam-se os modelos: eletroquímicos (Doyle, Fuller, e Newmann, 1993; Gu e Wang, 1996; Jorgerden e Haverkort, 2008), elétricos (Jorgerden e Haverkort, 2008; Hagemann, 1993; Brondani, 2015), estocásticos (Jorgerden e Haverkort, 2008; Chiasserini e Rao, 1999), analíticos (Jorgerden e Haverkort, 2008; Rakhmatov e Vrudhula, 2001; Rakhmatov, Vrudhula, e Wallach, 2002; Schneider, 2011), via Identificação de Sistemas (Romio, 2013; Machado, 2014) e, mais recentemente, híbridos (Kim, 2012; Fransozi, 2015). Dentre estes modelos, os analíticos descrevem a bateria de forma mais abstrata, modelando suas principais propriedades, com base em um conjunto reduzido de equações. Em geral, os modelos analíticos podem descrever descargas tanto contínuas, quanto variáveis no domínio do tempo, capturando, em muitos casos, efeitos não lineares do processo.
Da classe dos modelos analíticos, um dos modelos funcionais mais simples é baseado na Lei de Peukert (Peukert, 1897). Este modelo é computacionalmente eficiente e flexível, requerendo a avaliação de expressões analíticas, que podem ser configuradas para diferentes tipos de baterias (Jorgerden e Haverkort, 2008). Entretanto, se comparado a outros modelos mais acurados, o modelo baseado na Lei de Peukert apresenta um erro médio maior. Segundo Rakhmatov e Vrudhula (Rakhmatov e Vrudhula, 2001; Rakhmatov et al., 2002), as simulações da Lei de Peukert para predição do tempo de vida de baterias, quando comparadas às do programa simulador de baterias Dualfoil (DUALFOIL, 1993), considerando descargas constantes no tempo, apresentam um erro de médio de 6%. Em estudos realizados por Schneider (Schneider, 2011), aplicando a Lei de Peukert a partir de dados experimentais obtidos de uma bateria de Lithium-Ion (Li-Ion), sob descargas constantes, a mesma obteve um erro médio de 1,96%.
Inserido neste contexto, o Grupo de Automação Industrial e Controle (GAIC), da Universidade Regional do Noroeste do Estado do Rio Grande do Sul (Unijuí), tem realizado pesquisas (Brondani, 2015; Schneider, 2011; Romio, 2013; Machado, 2014; Fransozi, 2015) no intuito de verificar qual o modelo matemático é mais adequado para predizer o tempo de vida de baterias, sob diferentes especificações. Sendo assim, o principal objetivo deste trabalho é apresentar uma alternativa à formulação dinâmica do processo de descarga de baterias, propondo ajustes ao modelo baseado na Lei de Peukert, visando obter um modelo simples, de fácil implementação e simulação, com boa acurácia. Além disso, neste artigo é apresentada uma avaliação da extensão proposta ao modelo original, baseado em uma análise comparativa entre a simulação do modelo estendido e os dados experimentais de descargas de baterias de Li-Po – amplamente utilizadas como fonte de energia em dispositivos móveis –, em cenários de correntes constantes e variáveis.
O artigo está organizado conforme segue. Na Seção 2 são apresentadas considerações gerais sobre o modelo baseado na Lei de Peukert, bem como, o desdobramento algébrico da proposição de extensão a este modelo. Na Seção 3 é apresentada a metodologia utilizada para estimação dos parâmetros dos modelos, neste caso, a partir do método dos Mínimos Quadrados (MQ). Na Seção 4 são discutidos os resultados das simulações e as análises comparativas com os dados experimentais. E, por fim, na Seção 5 são apresentadas as considerações finais e as perspectivas para os trabalhos futuros.
Nesta seção é apresentado o modelo baseado na Lei de Peukert e, também, a proposição de extensão ao modelo original. Por definição, baterias são dispositivos que convertem a energia química armazenada em seua materiais constituintes em energia elétrica, por meio de uma reação de oxirredução eletroquímica. Nas baterias recarregáveis, a reversão desta reação (i.e., a recarga da bateria) é realizada através da conexão a uma fonte de energia. Na prática, a descarga de uma bateria possui características e efeitos não lineares – nível de cutoff, efeito de recuperação, taxa de capacidade, entre outros – que interferem diretamente no seu tempo de vida (Jorgerden e Haverkort, 2008).
Na modelagem matemática da descarga de uma bateria, dois fenômenos fundamentais precisam ser levados em conta, pois, afetam diretamente no tempo de vida e na quantidade de energia: o efeito da taxa de capacidade e o efeito de recuperação. Durante os períodos em que a corrente de descarga é reduzida significativamente, ocorre a relaxação da bateria, com isso, há uma reorganização dos elétrons ainda disponíveis. Assim, o efeito de recuperação amplia a capacidade da bateria em fornecer energia ao dispositivo, antes de atingir o limite mínimo de tensão elétrica (i.e, cutoff ) para manter o sistema em operação. O efeito de taxa de capacidade depende da capacidade atual da bateria e da intensidade da corrente de descarga aplicada. Em correntes altas a capacidade efetiva da bateria é reduzida, visto que não há tempo suficiente para que ocorra a reorganização das espécies eletroativas no interior na bateria, consequentemente reduzindo o seu tempo de vida. Ambos efeitos são mais fáceis de perceber em descargas com correntes variáveis no tempo (Schneider, 2011; Fransozi, 2015).
De aspecto empírico, a Lei de Peukert, proposta pelo engenheiro alemão Wilhelm Peukert, em 1897, descreve a relação que existe entre a vida útil e a taxa de descarga da bateria, considerando apenas o efeito da taxa de capacidade (Peukert, 1897). De acordo com a Lei de Peukert, o tempo de vida (L > 0), em horas (h), de uma bateria pode ser aproximado pela expressão
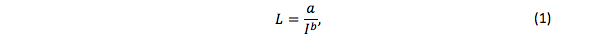
onde: I > 0 é a corrente de descarga, em ampère (A), e, a e b são parâmetros que dependem do tipo de bateria utilizado – e, são estimados a partir de dados experimentais; neste trabalho, utiliza-se o método dos Mínimos Quadrados (MQ) que será apresentado na Seção 3. Em uma bateria ideal, a teria que ser igual a capacidade da bateria, em ampère-hora (Ah), e b seria igual a 1. Na prática, a tem um valor próximo da capacidade da bateria, e b é um número superior a 1 (Schneider, 2011).
O modelo descrito pela equação (1) pode ser utilizado na predição do tempo de vida de baterias, submetidas ao processo de descargas com correntes constantes. Porém, segundo Rakhmatov e Vrudhula (Rakhmatov e Vrudhula, 2001; Rakhmatov et al., 2002), uma generalização da Lei de Peukert para correntes variáveis pode ser obtida, substituindo a corrente de descarga I pela média ponderada das correntes ao longo do tempo (t0 ≤ tk ≤ tn), como segue
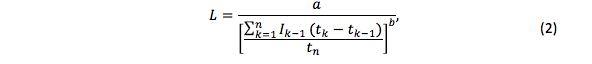
onde: Ik é o valor da corrente de descarga no tempo tk; e, a e b são os mesmos parâmetros estimados para o modelo da equação (1), conforme, a metodologia adotada por Rakhmatov e Vrudhula (Rakhmatov e Vrudhula, 2001). Além disso, para n = 1 a equação (2) se reduz a equação (1), que é o modelo original da Lei de Peukert.
O modelo original da Lei de Peukert, se comparado a outros modelos analíticos mais complexos – e.g., o Modelo de Difusão de Rakhmatov-Vrudhula – apresenta um erro médio de, aproximadamente, 2% para descargas com correntes constantes e, 8% para descargas com correntes variáveis (Rakhmatov e Vrudhula, 2001). Entretanto, utilizando a comparação das derivadas de 1a e 2a ordem da equação (1), em relação ao tempo, é possível estabelecer uma relação funcional f : I → L, de tal modo que o erro médio seja reduzido.
Da equação (1), evidenciando I à esquerda,


: Ik é o valor da corrente de descarga no tempo tk; e, C1, C2 e b são os mesmos parâmetros estimados para o modelo da equação (13), conforme, a metodologia adotada por Rakhmatov e Vrudhula (Rakhmatov e Vrudhula, 2001) para o modelo da equação (2). Além disso, para n = 1 a equação (15) se reduz a equação (13), que é o modelo estendido da Lei de Peukert.
Nesta seção é apresentada a estimação dos parâmetros a e b do modelo baseado na Lei de Peukert, e dos parâmetros C1, C2 e b do modelo proposto como extensão ao modelo original de Peukert. Estes parâmetros listados são específicos para cada tipo de bateria, sendo que para os ensaios laboratoriais foram utilizadas 8 baterias de Li-Po novas, modelo PL-383562-2C.
Os dados experimentais foram adquiridos a partir da plataforma de testes (i.e., testbed), localizada no Laboratório de Sensores Inteligentes (LSI) e, desenvolvida por integrantes do GAIC, da Unijuí (Nonemacher, Minelli, Sausen, e Sausen, 2010). A interface de gerenciamento da plataforma permite uma rápida configuração para a realização dos experimentos e possibilita realizar até quatro descargas simultâneas, armazenando as informações para cada descarga em arquivos separados, facilitando a consulta aos dados.
Todas as coletas de dados seguiram a mesma metodologia, tanto para o carregamento das baterias como para sua descarga, com o intuito de reduzir qualquer alteração no resultado final dos testes. Para as descargas constantes foram utilizados perfis diferentes, variando de 0,05 A a 0,8 A, com intervalos entre perfis contemplando correntes baixas, médias e altas. Cada perfil gerou, de modo individual, um tempo de descarga para cada bateria. A partir destes ensaios, foi possível calcular as médias de tempo de vida para cada descarga contínua (L¯). Os dados foram separados em dois conjuntos de dados, um para estimação de parâmetros (Iest e L¯est) – cf. Tabela 1, e outro para validação dos modelos (Ival e L¯val) – cf. Tabela 2.
Tabela 1. Dados para Estimação dos Parâmetros.
Iest (A) |
Lest (h) |
0,0500 |
15,6728 |
0,2500 |
3,0668 |
0,4500 |
1,6819 |
0,6000 |
1,2449 |
0,8000 |
0,9107 |
Inicialmente, desenvolvido por Carl Friedrich Gauss (1777-1855) e, mais tarde, generalizado por Pierre-Simon Laplace (1749-1827), o método dos MQ é uma técnica de otimização que busca encontrar o valor ótimo dos parâmetros para um determinado conjunto de dados, através da minimização da soma dos quadrados dos resíduos (Aguirre, 2007). Este método é dito linear quando a resolução de suas equações normais é possível através do uso de álgebra linear. Entretanto, muitos problemas não podem ser resolvidos linearmente – e.g., a estimação dos parâmetros dos modelos utilizados neste trabalho. Nestes casos, a técnica mais empregada é a linearização do problema, sendo então, o método MQ chamado não linear (Filho, 2013).
Uma formulação mais geral do método dos MQ, para problemas não lineares, pode ser expressa conforme segue. Seja y uma função de k parâmetros que deseja-se ajustar


A equação (26) está implementada no software de computação algébrica e numérica MatLab, na função de otimização lsqnonlin (MathWorks, 2015). Em um script M-file (i.e., linguagem própria do MatLab), foram implementadas as rotinas para estimação dos parâmetros dos dois modelos. Foram considerados os vetores Iest, Lest, α0 = [0,8;1]T , como aproximação inicial para Lei de Peukert e, β0 = [0;0,8;1]T , como aproximação inicial para o modelo proposto como extensão, na entrada da rotina para a função de otimização lsqnonlin. Os parâmetros encontrados foram: I) Para o modelo baseado na Lei de Peukert foram a = 0,7393 e b = 1,0195; II) Para o modelo proposto como extensão, os parâmetros obtidos foram C1 = −0,0004, C2 = 0,7369 e b = 1,0445.
Com o objetivo de validar os modelos, os resultados das simulações foram comparados com um conjunto de dados experimentais, obtidos através da plataforma de testes (cf. Tabela 2). Ambos modelos descreveram satisfatoriamente os dados experimentais, sendo que o modelo proposto apresentou um resultado mais acurado, com um erro médio de apenas 1,07%, já o modelo original apresentou um erro médio de 1,41%. O modelo proposto como extensão da Lei de Peukert, embora com um parâmetro a mais para estimação, obteve vantagem de 31% em termos de acurácia quando comparado ao modelo original.
Além disso, a proposição à Lei de Peukert obteve melhores resultados inclusive nos valores extremos (i.e., máximo e mínimo) de erro médio – que ocorrem nos perfis de 0,750 A e 0,625 A, respectivamente. Observa-se também que para os dois modelos, os erros de maior amplitude concentram-se nos perfis de descarga de correntes menores (i.e., I < 0,250 A), tal fato acontecesse porque em correntes baixas a bateria tem um tempo maior de descarga e consequentemente existe uma maior atuação dos efeitos não lineares na bateria, influenciando diretamente na determinação do seu tempo de vida.
Tabela 2. Resultado das Simulações dos Modelos.
Dados de Val. |
|
M. Peukert |
|
M. Peukert Ext. |
|||
Ival (A) |
Lexp (h) |
Lsim (h) |
Erro (%) |
Lsim (h) |
Erro (%) |
||
0,0750 |
10,1156 |
10,3687 |
2,5023 |
10,3512 |
2,3289 |
||
0,1250 |
6,4127 |
6,1595 |
3,9490 |
6,2616 |
2,3568 |
||
0,1750 |
4,5372 |
4,3708 |
3,6666 |
4,4460 |
2,0103 |
||
0,2250 |
3,3915 |
3,3829 |
0,2532 |
3,4325 |
1,2085 |
||
0,2750 |
2,7528 |
2,7570 |
1,1513 |
2,7888 |
1,3060 |
||
0,3250 |
2,3548 |
2,3252 |
1,2528 |
2,3449 |
0,4194 |
||
0,3750 |
2,0518 |
2,0096 |
2,0586 |
2,0207 |
1,5153 |
||
0,4250 |
1,8064 |
1,7688 |
2,0777 |
1,7739 |
1,7958 |
||
0,4750 |
1,5710 |
1,5792 |
0,5230 |
1,5799 |
0,5660 |
||
0,5250 |
1,4366 |
1,4260 |
0,7349 |
1,4234 |
0,9166 |
||
0,5750 |
1,2974 |
1,2997 |
0,4186 |
1,2946 |
0,2137 |
||
0,6250 |
1,1888 |
1,1938 |
0,1788 |
1,1868 |
0,1686 |
||
0,6750 |
1,0995 |
1,1037 |
0,3803 |
1,0953 |
0,3876 |
||
0,7250 |
1,0115 |
1,0262 |
1,4444 |
1,0166 |
0,4977 |
||
0,7750 |
0,9439 |
0,9587 |
1,5707 |
0,9482 |
0,4625 |
||
– |
Erro médio = 1,4108 |
Erro médio = 1,0769 |
|||||
Seguindo a mesma metodologia descrita na Seção 3, a partir de uma série de medições experimentais utilizando um smartphone, foram mensuradas as correntes em função de tarefas executadas pelo dispositivo. Deste modo, em seguida, definiu-se um perfil de descarga mais realístico, com variações da corrente ao longo do tempo, conforme a Tabela 3. Ao contrário das descargas contantes, este perfil possui variações ao longo do tempo, assim, os efeitos não lineares têm maior presença e, por consequência, o processo de descarga torna-se mais fiel ao perfil de utilização de um usuário.
Tabela 3. Ciclo do Perfil de Descarga Variável.
I (A) |
L (h) |
Descrição |
0,1000 |
0,0833 |
Chamada simples |
0,0100 |
0,0833 |
Stand by |
0,1500 |
0,0833 |
Chamada viva voz |
0,0100 |
0,0833 |
Stand by |
0,1000 |
0,0833 |
Visualizar imagem |
0,0100 |
0,0833 |
Stand by |
0,2000 |
0,1663 |
Acessar internet |
Os experimentos produziram um conjunto de valores de tempos de vida, para cada uma das baterias, conforme a Tabela 4. As simulações do modelo baseado na Lei de Peukert, indicaram um tempo de vida igual a 7,9485 h, sendo o erro médio 2,79%. Já para o modelo estendido da Lei de Peukert, o tempo de vida simulado foi de 7,8801 h, com um erro médio de 2,57%. O modelo proposto obteve uma acurácia 8,6% superior ao modelo original de Peukert. Ainda assim, tomando por base modelos de alta acurácia (e.g., o Modelo de Difusão de Rakhmatov-Vrudhula (Rakhmatov e Vrudhula, 2001)), o modelo estendido da Lei de Peukert apresenta um erro médio apropriado, dentro dos limites aceitáveis na literatura técnica (i.e., menor que 5%), já que por ser um modelo empírico, o efeito de recuperação, presente na descarga, não é considerado (Schneider, 2011).
Tabela 4. Resultados Experimentais para Descargas Variáveis.
Bateria |
Lexp (h) |
B1 |
7,7302 |
B2 |
8,5337 |
B3 |
7,8351 |
B4 |
8,1709 |
B5 |
7,7223 |
B6 |
8,2352 |
B7 |
7,8487 |
B8 |
7,8868 |
Média |
7,9954 |
Neste trabalho foram avaliados dois modelos baseados na Lei de Peukert, sendo um deles o modelo original e o outro uma proposta de extensão deste, utilizando perfis de descargas contínuas e variáveis para baterias de Li-Po. Tanto a Lei de Peukert, quanto o modelo proposto são funcionais e simples, computacionalmente flexíveis, e podem ser configurados para diferentes tipos de baterias. Além disso, ambos conseguem capturar a relação funcional não linear entre a vida útil e a taxa de descarga da bateria. Após a estimação dos parâmetros, foram realizadas simulações computacionais dos modelos e, em seguida, os resultados foram comparados com um conjunto de dados experimentais. Verificou-se, inicialmente, que para descargas constantes o modelo baseado na Lei de Peukert descreveu os dados experimentais com um erro médio de 1,41%. Já o modelo proposto, como extensão do modelo original de Peukert, descreveu satisfatoriamente os dados experimentais com erro médio de apenas 1,07% – acurácia próxima de modelos mais elaborados como, por exemplo, o Modelo de Difusão de Rakhmatov-Vrudhula. Destaca-se ainda que para descargas contínuas, o modelo proposto, obteve uma melhora de 31 % na predição do tempo de vida das baterias de Li-Po em relação ao modelo original.
Já para descargas variáveis, onde foi utilizado um perfil realístico de utilização de um smartphone, que possibilita que os efeitos não lineares fiquem mais evidentes, novamente o modelo proposto obteve um melhor desempenho quando comparado ao modelo original. O modelo baseado na Lei de Peukert apresentou um erro médio de 2,79%, enquanto o modelo proposto obteve um erro médio de 2,57%, o que representa uma redução de 8,6 % no erro médio quando da predição do tempo de vida de uma bateria. Como trabalhos futuros pretende-se ampliar o estudo comparativo adicionando-se uma variedade maior de perfis de descargas variáveis, possibilitando uma melhor distribuição entre cargas baixas, medias e altas, bem como comparar a acurácia do modelo proposto, neste trabalho, com outros modelos da literatura técnica sob este mesmo cenário e metodologia de análise.
Os autores agradecem à Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (Capes), pelo aporte financeiro recebido, e à Universidade Regional do Noroeste do Estado do Rio Grande do Sul (Unijuí), pela estrutura física oferecida.
Aguirre, L. A. (2007). Introdução à identificação de sistemas: técnicas lineares e não lineares aplicadas a sistemas reais (3. ed.). Belo Horizonte: UFMG.
Brondani, M. F. (2015). Modelagem matemática do tempo de vida de baterias de lítio íon polímero utilizando algoritmos genéticos (Dissertação). Universidade Regional do Noroeste do Estado do Rio Grande do Sul, Ijuí-RS.
Chiasserini, C. F., e Rao, R. R. (1999). Pulsed battery discharge in communication devices. In Proceedings of the 5th international conference on mobile computing and networking.
Doyle, M., Fuller, T., e Newmann, J. (1993, jan.). Modeling of galvanostatic charge and discharge of the lithium polymer insertion cell. Journal of Electrochemical Society, 140, 1526-1533.
DUALFOIL. (1993). Fortran programs for the simulation of electrochemical systems. Disponível em: http://www.cchem.berkeley.edu/jsngrp/fortran.html. (Acesso em: 9 jan. 2015)
Figueiredo, D. G., e Neves, A. F. (2005). Equações diferenciais aplicadas. Rio de Janeiro: IMPA.
Filho, K. S. O. (2013, abr.). Mínimos quadrados. Disponível em: http://astro.if.ufrgs.br/minq/. (Acesso em: 22 jul. 2015)
Fransozi, L. (2015). Modelagem matemática do tempo de vida de baterias de lítio íon polímero através de modelos híbridos (Dissertação). Universidade Regional do Noroeste do Estado do Rio Grande do Sul, Ijuí-RS.
Gu, W., e Wang, C. (1996). Thermal-electrochemical modeling of battery systems. Journal of Electrochemical Society, 143, 18-90.
Hagemann, S. C. (1993). Simple pspice models let you simulate common battery types. Electronic Design News, 38, 117-129.
Jorgerden, M. R., e Haverkort, B. (2008, jan.). Battery modeling (Tech. Rep.). Faculty Electrical Engineering.
Kim, T. (2012). A hybrid battery model capable of capturing dynamic circuit characteristics an nonlinear capacity effects (Dissertação). University of Nebraska, Lincoln-NE.
Machado, M. V. (2014). Modelagem matemática do tempo de vida de baterias utilizando modelos autorregressivos (Dissertação). Universidade Regional do Noroeste do Estado do Rio Grande do Sul, Ijuí-RS.
MathWorks. (2015). Optimization toolbox. Disponível em: http://www.mathworks.com/help/optim/index.html. (Acesso em: 19 jun. 2015)
Nonemacher, H. B., Minelli, L., Sausen, P. S., e Sausen, A. (2010). Desenvolvimento de um testbed para avaliação de modelos matemáticos utilizados na predição do tempo de vida de baterias. In Congresso regional de iniciação científica e tecnológica em engenharia.
Peukert, W. (1897). Über die abhängigkeit der kapazität von der entladestromstärke bei bleiakkumulatoren. Elektrotechnische Zeitschrift, 18, 287-288.
Rakhmatov, D., e Vrudhula, S. (2001). An analytical high-level battery model for use in energy management of portable electronic systems. In Proceedings of the international conference on computer aided design (iccad ’01).
Rakhmatov, D., Vrudhula, S., e Wallach, D. A. (2002). Battery lifetime prediction for energyaware computing. In Proceeedings of the 2002 international symposium on low power electronics and design (islped ’02).
Romio, L. C. (2013). Modelagem matemática do tempo de vida de baterias utilizando a teoria de identificação de sistemas (Dissertação). Universidade Regional do Noroeste do Estado do Rio Grande do Sul, Ijuí-RS.
Schneider, K. K. (2011). Modelos matemáticos na predição do tempo de vida de baterias utilizadas em dispositivos móveis (Dissertação). Universidade Regional do Noroeste do Estado do Rio Grande do Sul, Ijuí-RS.
1. Douturando do PPG em Modelagem Matemática, Unijuí, Ijuí-RS Email: douglasjoziel@outlook.com
2. Prof. Dr. do PPG em Modelagem Matemática, Unijuí, Ijuí-RS
3. Profa. Dra. do PPG em Modelagem Matemática, Unijuí, Ijuí-RS
4. Prof. Dr. do PPG em Modelagem Matemática, Unijuí, Ijuí-RS