

Vol. 38 (Nº 16) Año 2017. Pág. 29
Caroline Maiara de JESUS 1; Eder Pereira MIGUEL 2; Alba Valéria REZENDE 3; Ricardo de Oliveira GASPAR 4; Alcides GATTO 5; Marco Bruno Xavier VALADÃO 6; João Victor Nobre CARRIJO 7
Recibido: 02/12/16 • Aprobado: 19/12/2016
RESUMO: O objetivo deste trabalho foi testar funções de densidade de probabilidade para a distribuição das variáveis diâmetro, altura total, área transversal e volume individual, em um povoamento de eucalipto. As funções de densidade de probabilidade (fdp) testadas foram Gamma, Beta, Weibull 3P, Normal, Log-Normal e Dagum. Os dados foram provenientes de um povoamento de Eucalipto Urograndis, com seis anos de idade, localizado na Fazenda Água Limpa, pertencente à Universidade de Brasília – UnB. Foram amostradas de forma aleatória 41 parcelas de 100 m², na qual foram medidos todos os diâmetros e a altura total das árvores que compunham as parcelas. Para avaliar a aderência dos dados amostrados as fdp utilizou-se o teste de Kolmogorov-Smirnov e as estatísticas de ajuste precisão: Erro padrão da estimativa em porcentagem (Syx%), Coeficiente de determinação ajustado (R² ajustado), soma das frequências estimadas e análise gráfica das fdp’s. Para a variável diâmetro a função densidade de probabilidade que melhor se ajustou foi a Beta, para a área seccional foi a função Dagum, para o volume foi a função densidade de probabilidade Weibull 3P e para a altura total nenhuma das funções foram aderentes aos dados. |
ABSTRACT: The main objective of this study was to test the probability density functions for the distribution of the variables: diameter, total height, cross-section area and individual tree volume, in an Eucalyptus forest stand. The Functions tested were Gamma, Beta, Weibull 3P, Normal, Log-Normal and Dagum. The data were from an Eucalipto Urograndis afforestation, seven years old, located at Fazenda Água Limpa from University of Brasília-UnB. On the area were sampled randomly, 41 plots of 100m², where all the trees were measure in diameter at breast height and total height. To evaluate the data adherence was used the Kolmogorov-Smirnov test. The choice for the best model was based on the results of the standard error in percentage (Syx%), on the adjusted coefficient of determination (R² adjusted) and graphical analyses of the PDF’s. For the diameter variable the probability density function that most set was Beta, for cross-section area was Dagum function, for individual tree volume Weibull 3P and finally for total height none of the functions were adherent to the data. |
O desenvolvimento de estudos voltados para a otimização da produção de eucalipto visando atender às exigências e necessidades do mercado consumidor é de extrema importância. Para isso, é necessário quantificar e prognosticar os estoques da floresta, a fim de definir a utilização dos bens advindos da mesma e obter informações para possíveis tomadas de decisão. Dados de diâmetro, altura, área basal e volume das árvores são importantes nas estimativas dos estoques, presente e futuro da produção de madeira de uma floresta. Tais estimativas podem ser obtidas por meio de funções de produção e controle de densidade (NETTO, 2008). A análise da distribuição das variáveis pode ser feita por meio de modelagem, conhecidos como modelos de distribuição.
Um modelo de prognose pode ser do tipo determinístico ou aleatório, alguns desses modelos exprimem condições correntes e futuras e são chamados modelos de crescimento e produção (WOLFF, 2012). Segundo CAMPOS & LEITE (2013), de acordo com o nível de detalhe desejado, os modelos de crescimento e produção podem ser classificados em modelos em nível de povoamento, modelos em nível de árvores e modelos de distribuição.
Os modelos de distribuição são definidos por uma função de densidade de probabilidade (fdp), sendo comum o uso da distribuição diamétrica devido à sua eficácia e simplicidade para demonstrar a estrutura de um povoamento florestal, porém, podem ser utilizadas as distribuições em altura, área transversal e volume. Uma fdp define a probabilidade associada a cada valor da variável de estudo descrevendo a distribuição relativa ou absoluta dos diferentes tamanhos de árvores (CAMPOS & LEITE, 2013). As funções que se destacam são: Gamma, Beta, Weibull, Normal e Log-Normal, as quais permitem que se obtenha uma probabilidade de ocorrência das árvores dentro de intervalos de classe com limite inferior e superior (SCOLFORO, 2006).
Para avaliar a qualidade de ajustamento produzida pelas funções de densidade probabilística são utilizados testes que verificam o índice de aderência, ou seja, que testam a concordância entre a frequência observada e estimada por uma função de densidade, considerando um dado nível de probabilidade de erro (NETTO, 2008). Entre estes testes está o de Kolmogorov – Sminov que compara a frequência estimada acumulada com a observada acumulada.
Portanto, conhecendo a estrutura de um povoamento é possível avaliar o comportamento de uma espécie, levando em consideração os fatores que interferem em seu crescimento. Além disso, corrobora com a análise das distribuições das variáveis de interesse, possibilitando estimar o número de árvores por hectare, por classe de diâmetro e a altura média para cada classe.
Várias funções de densidade de probabilidade têm sido usadas na área florestal visando descrever a distribuição diamétrica de uma floresta como em NETTO (2008), FERREIRA (2011), STEPKA et al. (2011), BINOTI et al. (2012), JUNIOR et al. (2013) e SCHIKOWSKI et al. (2016), sendo bastante comum relacionar a distribuição diamétrica de florestas equiâneas com a função densidade de probabilidade Normal, porém, outras funções podem descrever de maneira mais eficiente essa distribuição.
Além disso, são poucos os trabalhos que analisam a distribuição de altura de árvores de um povoamento bem como de outras variáveis, como área seccional e volume, podendo citar trabalhos de ALVES et al. (2007), NETO et al. (2014), SANTOS et al. (2015) e MACHADO et al. (2010).
Seria a distribuição de frequência dessas variáveis igualmente eficientes e precisas para estimar a estrutura de um povoamento, tal como é comprovado para o diâmetro? E qual função de densidade de probabilidade melhor descreve cada uma destas variáveis? Diante dessas indagações, o objetivo desse estudo foi aplicar o conceito de função densidade de probabilidade para explicar o comportamento da distribuição das variáveis diâmetro, altura total, área seccional e volume individual da floresta em um povoamento de eucaliptos no Distrito Federal, ajustando, testando e selecionando modelos de distribuição contínua para as variáveis em questão.
O experimento foi conduzido na Fazenda Água Limpa, pertencente à Universidade de Brasília – UnB, situada a uma altitude média de 1.080 metros, em um plantio clonal de híbrido de Eucalyptus urophylla x Eucalyptus grandis, clone I224, conhecido como Eucalipto Urograndis. A área total do povoamento é de 3,29 hectares, plantado com espaçamento 3 x 2 m, e possui seis anos de idade. As coordenadas e a localização da área podem ser vistas na Figura 1.
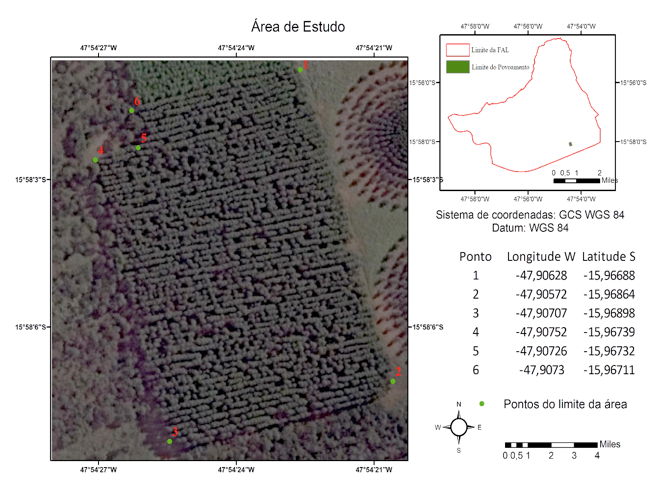
Figura 1: Localização do povoamento de Eucalipto Urograndis, no Distrito Federal.
De acordo com o Sistema Brasileiro de Classificação de Solos da Embrapa (2009), o solo na área do plantio é um Latossolo Vermelho. O clima corresponde ao tipo Aw, tropical úmido, segundo a classificação de KÖEPPEN, com temperatura máxima de 28,5°C e mínima de 12°C. A precipitação média anual é de 1500 mm, com pronunciada estação seca de Julho a Setembro.
Para a obtenção dos dados foram lançadas ao acaso 41 parcelas de 10 x 10 metros (100 m² de área cada). A variável diâmetro à altura do peito (DAP) foi mensurada em cada árvore da parcela com o auxílio de fita métrica. A variável altura total foi obtida utilizando o hipsômetro Suunto.
A variável volume foi obtida a partir da cubagem rigorosa usando o método de Smalian. Foram cubadas 50 árvores respeitando-se a proporcionalidade das classes de diâmetro. Para obter o volume real de todas as árvores amostradas foi ajustado o modelo volumétrico proposto por SCHUMACHER & HALL (1933). Segundo CAMPOS & LEITE (2013) esse é um dos modelos mais difundidos na área florestal, uma vez que suas propriedades estatísticas resultam em estimativas quase sempre não tendenciosas. Para definir o número de classes das variáveis utilizou-se a fórmula de Sturges
As funções de densidade de probabilidade Gamma, Beta, Weibull 3P, Normal, Log-Normal e Dagum foram ajustadas para obter a frequência de distribuição das variáveis diâmetro, altura total, área transversal e volume individual (Tabela 1) utilizando o software Microsoft Office Excel 2010. Para a obtenção dos coeficientes das equações de fdp’s foi utilizado o software EasyFit. O ajuste foi feito considerando todas as árvores, amostradas nas 41parcelas.
Tabela 1: Funções de densidade de probabilidade ajustadas para descrever a distribuição das variáveis diâmetro,
altura total, área seccional e volume individual de um povoamento de Eucalipto Urograndis no Distrito Federal.

Para a comparação da eficiência das diferentes distribuições utilizou-se o teste de aderência Kolmogorov-Smirnov. Após o agrupamento das árvores em classes diamétricas, classes de altura, classes de área seccional e classes de volume, foi comparada a frequência observada com a estimada pelos modelos.
Para a escolha da fdp que melhor descreve a estrutura em diâmetro, altura total, área seccional e volume individual do povoamento realizou-se um ranqueamento, considerando os valores do teste de Kolmogorov-Smirnov, Syx% e R² ajustado, para isso as funções foram colocadas em ordem de 1 a 6 de acordo com os melhores resultados estatísticos. Por último realizou-se a análise gráfica das funções, comparando a distribuição original com as funções densidade de probabilidade.
O teste de aderência Kolmogorov-Smirnov é bastante utilizado na área florestal, principalmente em estudos de comparação de modelos de distribuição e produção de povoamentos florestais em geral, podendo citar SILVA (2003), GOMIDE et al. (2009), JUNIOR et al. 2010, TÉO et al. 2011, STEPKA et al. (2011), EBLING et al. (2014), BINOTI et al. (2014) e SANTOS et al. (2015). É um teste não paramétrico e uma das vantagens de utiliza-lo é que estes são menos exigentes do que os outros, dispensando a normalidade nos dados, além disso, eles independem da forma da população da qual a amostra foi obtida e por último eles são de mais fácil aplicação e exigem menor volume de cálculos VIALI (2008).
O erro padrão da estimativa indica quão próximos os valores estimados estão dos valores observados. Quanto mais próximo de zero mais preciso será o modelo. Pelo coeficiente de determinação ajustado foi identificado o quanto a variação total é explicada pelo modelo. Quanto maior o valor encontrado, melhor será o ajuste.
A seleção da melhor função de densidade de probabilidade deu-se primeiramente com a verificação da aderência e posteriormente com a análise da função que apresentou menor erro padrão da estimativa em porcentagem (Syx%) e melhor coeficiente de determinação ajustado (R²ajustado).
A partir das estatísticas descritivas das variáveis dendrométricas do povoamento estudado observou-se que o diâmetro por árvore variou de 5,12 cm até 22 cm, a altura total de 5 m à 27,75 m, a área seccional de 0,002 m² até 0,038 m² e o volume de 0,007 m³ à 0,497 m³. Esses resultados são característica de um povoamento heterogêneo, o que se relaciona ao regime de manejo do povoamento e a ausência de tratos silviculturais. O diâmetro apresentou 9 classes com amplitude entre as mesmas de 2 cm, a altura 8 classes com amplitude de 3 m, a área seccional 12 classes com amplitude de 0,0035 m² e o volume 10 classes com 0,05 m³.
Fica evidenciado que para as variáveis diâmetro, área seccional e volume existe maior concentração de indivíduos nas classes centrais da distribuição, no entanto, para a variável altura a frequência de árvores é superior nas classes finais. Essa característica pode ser explicada pela idade do povoamento florestal estudado. Analisando os resultados pode-se afirmar que o povoamento em estudo é caracterizado como uma distribuição unimodal, já que não existiram intervenções silviculturais entre as classes diamétricas existentes.
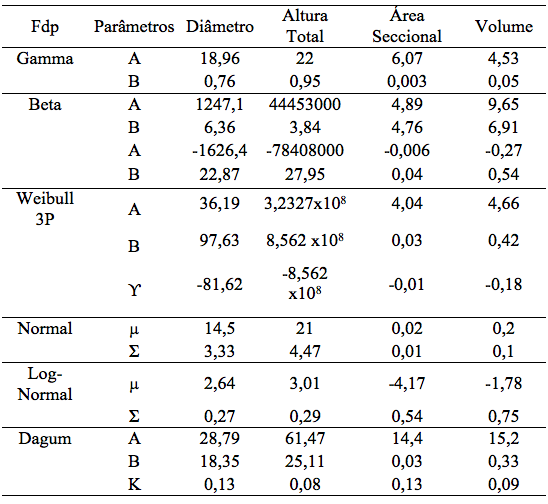
Os valores da estimativa dos parâmetros das funções de distribuição de densidade de probabilidade Gamma, Beta, Weibull 3P, Normal, Log-Normal e Dagum para as variáveis estudadas estão apresentados na Tabela 2. O ajuste destas funções foi realizado no software EasyFit, através do método de máxima-verossimilhança. Sequencialmente com os parâmetros obtidos utilizou-se o Microsoft Office Excel 2010 para os demais processamentos das funções como estatísticas de ajuste e precisão e confecção do gráfico das frequências observadas pela estimada.
Tabela 2: Estimativa dos parâmetros das distintas funções de densidade de probabilidade
(fdp’s) em um povoamento de Eucalipto Urograndis.
Para selecionar a função de densidade de probabilidade (fdp), que melhor representa a distribuição da variável diâmetro, foram analisadas as aderências das funções pelo teste de Kolmogorov-Smirnov (K-S) e, posteriormente, verificadas as estatísticas de ajuste e precisão, ou seja, coeficiente de determinação ajustado (R² ajustado) e erro padrão da estimativa em porcentagem (Syx%), conforme exposto na Tabela 3.
Tabela 3:
Valores do teste de Kolmogorov-Smirnov, erro padrão da estimativa em porcentagem e coeficiente de determinação
ajustado para diferentes funções de densidade de probabilidade (fdp’s) em povoamento de Eucalipto Urograndis no Distrito Federal.
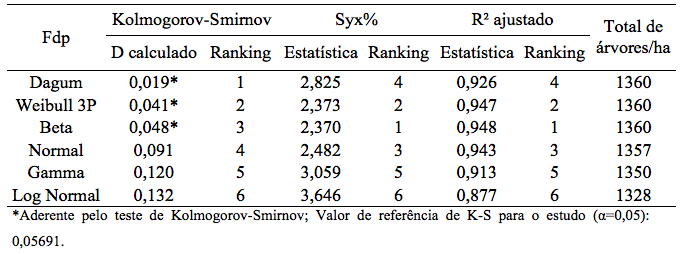
Observando os resultados do teste de Kolmogorov-Smirnov, somente as funções Dagum, Beta e Weibull 3P apresentaram aderência para os dados, portanto, apenas essas funções conseguiram representar a distribuição diamétrica no povoamento. As funções Gamma, Normal e Log-Normal não se aderiram. Esses resultados podem ser corroborados na Figura 2, na qual verifica-se o comportamento das funções em descrever a distribuição dos diâmetros.
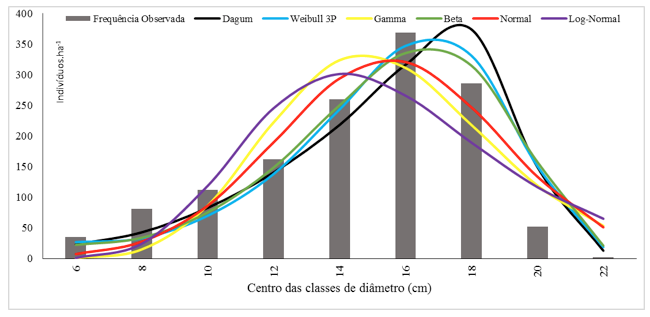
Figura 2: Comportamento das funções de densidade de probabilidade na descrição da distribuição
em classes de diâmetro em um povoamento de Eucalipto Urograndis no Distrito Federal.
Analisando os gráficos das distribuições probabilísticas é possível perceber visualmente a superioridade das distribuições que se aderiram ao povoamento de estudo (Beta, Weibull 3P e Dagum). Verifica-se que todas apresentaram comportamentos semelhantes com ligeira tendência em subestimar os indivíduos nas menores classes e superestimar nas classes de maior diâmetro.
ARCE (2004) estudando as distribuições diamétricas, em um povoamento de clones de Populus deltoides, verificou que todas as distribuições por ele analisadas (Normal, Gamma, Beta, Sb de Johnson e Weibull 3P) apresentaram resultados satisfatórios, o que assemelha-se, em parte, com os obtidos neste estudo.
A Tabela 3 mostra que as funções aderentes apresentam estatísticas de ajuste e precisão muito próximas, sendo que a função Beta se sobresaiu as demais. Porém, tanto a função Weibull 3P como a função Dagum podem ser utilizadas para descrever o comportamento da distribuição em classes de diâmetros deste povoamento conforme as estatísticas de aderência e de precisão.
Dentre as diversas funções de densidade de probabilidade utilizadas para descrever a variável diâmetro em povoamentos florestais, funções como Weibull 3P e a Beta se destacam em diversos trabalhos. FERREIRA (2011) estudou o comportamento da estrutura diamétrica em povoamentos de florestas plantadas, LUREIRO et al. (2013) analisaram a distribuição diamétrica para um povoamento de Araucaria angustifolia, no Paraná, e ORELLANA et al. (2014) realizaram a modelagem da distribuição diamétrica de espécies florestais em um fragmento de floresta Ombrófila Mista, localizada na Floresta Nacional de Irati.
No presente estudo a função Dagum também foi aderente, apresentando estatística de ajuste e precisão satisfatória para descrever a variável em questão, todavia, esta função é pouco usual no meio florestal, embora, tenha demonstrado aderência em trabalhos como SCHIKOWSKI et al. (2016) que descreveram o comportamento da distribuição diâmétria de um povoamento de Araucaria angustifolia em um remanescente de floresta Ombrófila mista no Paraná, corroborando aos resultados encontrados nesta pesquisa.
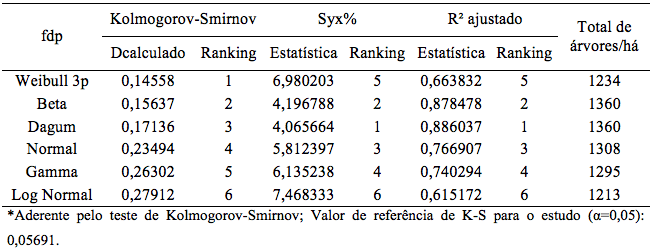
Para de selecionar a função de densidade de probabilidade (fdp), que melhor representa a distribuição da altura total, analisou-se os resultados das aderências das funções pelo teste de Kolmogorov-Smirnov (K-S) e, posteriormente, foram verificadas as estatísticas de ajuste e precisão, coeficiente de determinação ajustado (R² ajustado) e erro padrão da estimativa em porcentagem (Syx%), conforme exposto na Tabela 4.
Tabela 4: Valores do teste de Kolmogorov-Smirnov, erro padrão da estimativa em porcentagem e coeficiente de determinação ajustado para diferentes funções de densidade de probabilidade (fdp’s) em povoamentos de Eucalipto Urograndis no Distrito Federal.
Embora alguns estudos conseguiram demonstrar aderência entre as funções de densidade de probabilidade para a variável altura, tais como, MACHADO et al. (2010) e NETO et al. (2014), no presente trabalho tal aderência não foi verificada em nenhuma das funções citadas (Figura 3), indicando assim que outras funções deveriam ser testadas ou mesmo que o regime de manejo e a ausência de tratos silviculturais, no povoamento em estudo, fizeram com que nenhuma das funções se aderissem, e, por fim, este resultado ocorreu devido a características intrínsecas do povoamento.
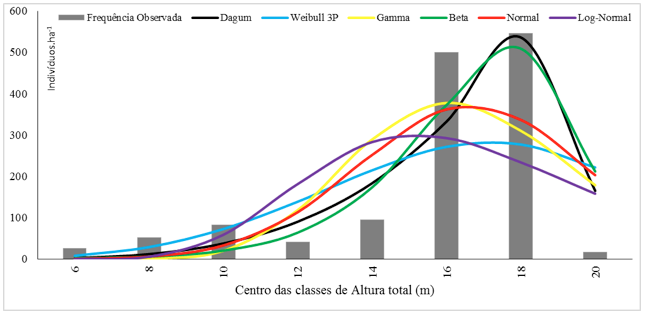
Figura 3 : Comportamento das funções de densidade de probabilidade na descrição da distribuição em classes
de altura total em um povoamento de Eucalyptus urograndis no Distrito Federal.
Para selecionar a função de densidade de probabilidade (fdp), que melhor representa a distribuição da variável área seccional, também foram analisadas as aderências das funções pelo teste de Kolmogorov-Smirnov (K-S) e, posteriormente, verificadas as estatísticas de ajuste e precisão, coeficiente de determinação ajustado (R² ajustado) e erro padrão da estimativa em porcentagem (Syx%), conforme exposto na Tabela 5.
Tabela 5: Valores do teste de Kolmogorov-Smirnov, erro padrão da estimativa em porcentagem e coeficiente de determinação ajustado
para diferentes funções de densidade de probabilidade (fdp’s) em povoamentos de Eucalyptus urograndis no Distrito Federal.
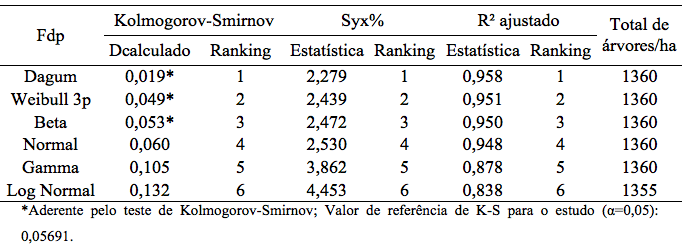
Observando os resultados do teste aderência Kolmogorov-Smirnov, é possível inferir que somente as funções Dagum, Beta e Weibull 3P apresentaram aderência para os dados da variável área seccional, indicando que somente essas funções conseguiram representar a distribuição para esse atributo dos clones de Eucalyptus urograndis, resultado este já esperado haja vista que estas mesmas funções foram aderentes para a vaiável diâmetro, a qual está intrinsicamente ligada com a área seccional. As funções Gamma, Normal e Log-Normal não se aderiram a este povoamento. Esses resultados podem ser corroborados pela Figura 4, na qual verifica-se o comportamento das funções para descrever a distribuição da variável.
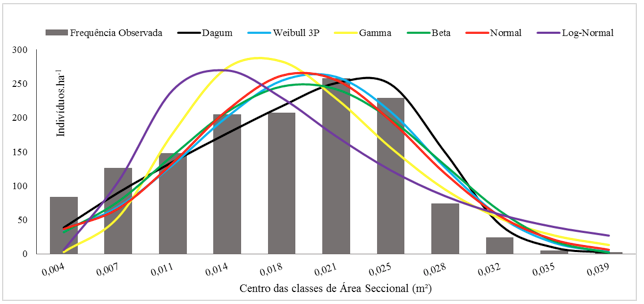
Figura 4 : Comportamento das funções de densidade de probabilidade na descrição da distribuição em classes
de área seccional em um povoamento de Eucalipto Urograndis no Distrito Federal.
Analisando a Figura 4 possível perceber visualmente a adequação das funções aderentes para a variável do povoamento estudado. Verifica-se que todas subestimaram os indivíduos nas menores classes e superestimaram nas maiores classes da variável área seccional.
Ao analisar a Tabela 5 observa-se que as funções aderentes apresentam estatísticas de ajuste e precisão semelhantes, sendo que a função Dagum se sobresaiu as demais. Porém, tanto a função Weibull 3P como a função Beta podem ser utilizadas para descrever o comportamento da distribuição em classes de área seccional deste povoamento, conforme as estatísticas de aderência e de precisão. Não é comum encontrar na literatura estudos que utilizem a função Dagum para descrever a distribuição da área seccional.
Dentre os poucos trabalhos realizados para descrever a distribuição da variável área seccional, em povoamentos florestais, é possível destacar o estudo de MACHADO et al. (2010), que obteve resultados de aderência semelhantes a este trabalho.
Considerando que a variável área seccional tem alta correlação com o volume, sendo possível ajustar funções volumétricas, e, levando em consideração que a partir da área seccional é possível realizar a projeção da área basal, em nível de povoamento, justifica-se a realização de novos estudos para gerar maior conhecimento sobre a distribuição dessa variável.
Para selecionar a função de densidade de probabilidade (fdp), que melhor representa a distribuição do volume individual, foram analisados os resultados das aderências das funções pelo teste de Kolmogorov-Smirnov (K-S) e, posteriormente, verificadas as estatísticas de ajuste e precisão, coeficiente de determinação ajustado (R² ajustado) e erro padrão da estimativa em porcentagem (Syx%), conforme exposto na Tabela 6.
Tabela 6: Valores do teste de Kolmogorov-Smirnov, erro padrão da estimativa em porcentagem e coeficiente de determinação
ajustado para diferentes funções de densidade de probabilidade (fdp’s) em povoamentos de Eucalipto Urograndis no Distrito Federal.
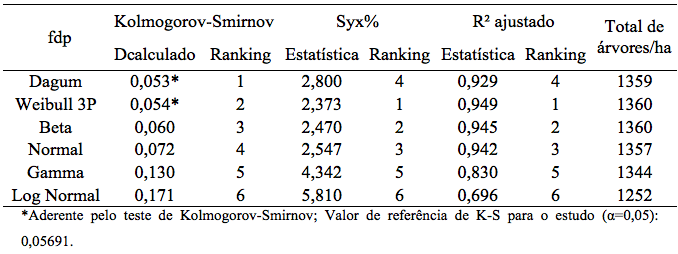
Analisando os resultados do teste aderência Kolmogorov-Smirnov, é possível observar que somente as funções Dagum e Weibull 3P apresentaram aderência para o atributo volume individual, indicando que somente essas funções conseguiram representar a distribuição para essa variável no povoamento estudado. As funções Gamma, Beta, Normal e Log-Normal não se aderiram a este povoamento para essa variável. Esses resultados podem ser corroborados pela Figura 5, na qual verifica-se o comportamento das funções para descrever a distribuição do volume individual.
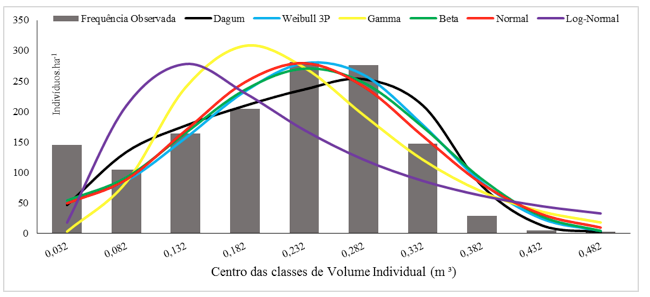
Tabla 5 : Comportamento das funções de densidade de probabilidade na descrição da
distribuição em classes de volume individual em um povoamento de Eucalipto Urograndis no Distrito Federal.
Analisando os resultados das distribuições probabilísticas é possível perceber visualmente a superioridade das distribuições que se aderiram ao povoamento de estudo (Weibull 3P e Dagum). Verifica-se que essas funções apresentaram comportamentos diferenciado nas classes iniciais da distribuição, a função Weibull 3P apresentou ligeira tendência em subestimar os indivíduos, enquanto que a função Dagum superestimou. Nas classes de maior diâmetro as duas funções superestimaram ligeiramente a frequência real.
Ao analisar a Tabela 6 verifica-se que as funções aderentes apresentam estatísticas de ajuste e precisão muito próximas, sendo que a função Weibull 3P se apresentou superior à função Dagum.
Poucos são os estudos onde as funções de densidade de probabilidade são utilizadas para descrever a variável volume individual em povoamentos florestais, embora, tal resultado corrobora com o obtido por MACHADO et al. (2010) no qual trabalhando em um povoamento de Araucaria angustifolia identificou a distribuição do volume individual utilizando funções de densidade de probabilidade.
O modelo que melhor descreveu a variável diâmetro foi a função de densidade de probabilidade Beta, porém, as fdp’s Dagum e Weibull 3P também foram aderentes, apresentando estatísticas de ajuste e precisão semelhantes.
No estudo da variável altura total nenhuma das funções testadas mostraram-se aderentes, indicando que novas funções precisam ser testadas ou que o regime de manejo e ausência de tratos silviculturais neste povoamento comprometeram a aderência das funções testadas para descrever sua estrutura vertical;
Para a área seccional as funções Beta, Dagum e Weibull 3P mostraram aderência em suas distribuições em classes com uma ligeira superioridade da função Dagum;
A função Weibull 3P foi a que melhor representou a variável volume, apresentando aderência pelo teste de K-S. A função Dagum também foi aderente, porém, foi ligeiramente inferior à Weibull 3P; e
As funções Gamma, Normal e Log-Normal não mostraram aderência em nenhum dos atributos (diâmetro, altura total, área seccional e volume individual) estudados no povoamento.
Alves, F. T.; Brandão, C. F. L. E S; Rocha, K. D. Da; Silva, J. T. Da; Marangon, L. C.; y Ferreira, R. L. C. (2007) Estrutura diamétrica e hipsométrica do componente arbóreo de um fragmento de Mata Atlântica, Recife-PE. Cerne, Vol. 13, núm. 1, pp. 83-95.
Arce, J. E. (2004) Modelagem da estrutura de florestas clonais de Populus deltoides March através de distribuições diamétricas probabilísticas. Ciência Florestal, Santa Maria, Vol. 14, núm. 1, pp. 149-164.
Binoti, D. H. B; Binoti, M. L. M. S; Leite, H. G; Fardin, L; Oliveira, J. C. (2012) Probability density functions for description of diameter distribution in thinned stands of Tectona grandis. Cerne, Vol. 18, núm.2, pp.185-196.
Binoti, M. L. M. S; Binoti, D. H. B; Leite, H. G; Silva, A. A. L. Da; Pontes, C. (2014). Utilização de redes neurais artificiais para a projeção da distribuição diamétrica de povoamento equiâneos. Revista Árvore, Viçosa, Vol.38, núm.4, pp.747-754.
Campos, J. C. C.; Leite, H. G. (2013). Mensuração florestal: perguntas e respostas. 4.ed. Viçosa, pp. 605.
Ebling, A. A; Pelissari, A. L; Abrão, S. F; Bamberg, R. (2014). Prognose da estrutura diamétrica de remanescente de floresta com Araucária utilizando a função densidade de probabilidade Weibull. Revista Agro, Vol. 8, núm. 1, pp. 112-118.
Ferreira, J.C.S. (2011) Análise da estrutura diamétrica em povoamentos de florestas plantadas a partir de funções de densidade de probabilidade. Dissertação de Mestrado, UNB, pp. 116.
Gomide, L. R; Scolforo, J. R. S; Oliveira, A. D. De. (2009) Análise das estruturas diamétrica e hipsométrica de fragmentos florestais localizados na bacia do rio São Francisco, em Minas Gerais, Brasil. Floresta, Curitiba, PR. Vol.39, núm.2, pp. 239-251.
Junior, C.A.A; Nogueira, G. S; Oliveira, M. L. R. De, Miranda, R. O. V De; Castro, R. V. O; Pelli, E. (2010). Projeção da distribuição diamétrica de povoamentos de eucalipto em diferentes amplitudes de classe. Pesquisa Agropecuária Brasileira, Vol. 45, núm. 11, p. 1275-1281.
Junior, C. A. A; Leite, H. G; Castro, R. V. O; Binoti, D. H. B; Alcântara, A. E. M. De; Binoti, M. L. M. Da S. (2013) Modelagem da distribuição diamétrica de povoamentos de eucalipto utilizando a função gama. Cerne, Lavras, Vol. 19, núm. 2, pp. 307-314.
Loureiro, G.H; Curto, R. De A; Netto, S. P; Rosot, N.C; Marongon, G. P. (2013) Ajuste de funções de distribuição diamétrica para um povoamento de Araucaria angustifólia (Bert.) O. Ktze antes e após desbaste. ENCICLOPÉDIA BIOSFERA, Centro Científico Conhecer, Vol.9, núm.16, pp. 56-68.
Machado, S. A; Nascimento, R. G. M; Miguel, E.P; Téo, S. J; Augustynczik, A. L. D. (2010). DISTRIBUTION OF TOTAL HEIGHT, TRANSVERSE AREA AND INDIVIDUAL VOLUME FOR Araucaria angustifolia (Bert.) O. Kuntze. Cerne, Lavras, Vol. 16, núm. 1, pp. 12-21.
Neto, S. P. De M; Pulrolnik, K; Vilela, L; Marchão, R. L; Junior, R. G; Maciel, G. A. (2014). Distribuição diamétrica e altimétrica do híbrido Eucalyptus urophylla x Eucalyptus grandis em sistema agrossilvipastoril. EMBRAPA Cerrados, pp. 27.
Netto, C, C. (2008). Dinâmica da distribuição diamétrica de povoamentos de Pinus taeda L. em diferentes idades e espaçamentos. Dissertação (mestrado em Engenharia Florestal) – Universidade de Santa Maria, Santa Maria, RS, pp. 106.
Orellana, E. (2009). Funções densidade de probabilidade no ajuste da distribuição diamétrica de um fragmento de floresta ombrófila mista. UNICENTRO, pp. 122.
Santos, R. O. Dos; Lima, R. B. De; Abreu, J.C. De; Aparício, P. Da S.; Oliveira, C. P. De. (2015) Modelagem da distribuição em altura de Eschweilera coriacea (DC.) S.A. Mori em uma floresta ombrófila densa, Amapá, Brasil. CONTECC, pp. 4.
Schikowski, A. B; Martins, A. P. M; Schiavo, B. N. De V; Stang, M. B; Corte, A. P. D; Netto, S. P; Sanquetta, C. R. (2016). Dinâmica da distribuição diamétrica de Araucaria angustifólia em um remanescente de floresta ombrófila mista no Paraná. Revista Bras. Biom., Lavras, Vol.34, núm. 1, pp. 163-182.
Scolforo, J. R. S. (2006) Biometria florestal: modelos de crescimento e produção florestal, LAVRAS: UFLA/FAEPE, pp. 393.
Silva, E. Q. da. (2003) Nova função de densidade de probabilidade aplicável à Ciência Florestal. pp. 98.
Stepka, T. F; Lisboa, G. Dos S; Kurchaidt, S. M. (2011). Funções densidade de probabilidade para a estimativa da distribuição diamétrica em povoamento de Eucalyptus sp na região centro-sul do Paraná. Guarapuva, PR, Vol. 7, núm.3 , pp. 429-439.
Schumacher, F. X.; Hall, F. S. (1933) Logarithmic expression of timber-tree volume. Journal of Agricultural Research, Vol.47, núm.9, pp.719-734.
Téo, S. J; Rocha, S. P. Da; Bortoncello, A. C; Paz, R. A; Costa, R. H. Da. (2011) Dinâmica da distribuição de povoamentos de Pinus taeda, na região de Caçador, SC. Pesquisa Florestal Brasileira, Colombo, Vol.31, núm. 67, pp. 183-192.
Viali, L. (2008). Teste de hipóteses não paramétricos. UFRGS. pp.43.
Weber, S. H. (2006) Desenvolvimento de nova função densidade de probabilidade para avaliação de regeneração natural. Universidade Federal do Paraná, Curitiba, pp. 87.
Wolff II, N. I. (2012) Modelagem do crecimento e da produção de Pinus taeda L.UNICENTRO, Irati-PR, pp. 62.
1. Engenheira Florestal pela Universidade de Brasília – UNB E-mail: cmaiara@yahoo.com.br
2. Professor Adjunto do departamento de Engenharia Florestal da Universidade de Brasília - UnB. É professor do programa de Pós-graduação em Ciências Florestais da UnB. Email: edermiguel@unb.br
3. Professora Associada do departamento de Engenharia Florestal da Universidade de Brasília - UnB. É professora do programa de Pós-graduação em Ciências Florestais da UnB. Email: albavr@unb.br
4. Professor Adjunto do departamento de Engenharia Florestal da Universidade de Brasília - UnB. É professor do programa de Pós-graduação em Ciências Florestais da UnB. Email: ricogaspar@unb.br
5. Professor Adjunto do departamento de Engenharia Florestal da Universidade de Brasília - UnB. É professor do programa de Pós-graduação em Ciências Florestais da UnB. Email: alcidesgatto@unb.br
6. Aluno de doutorado do Programa de Pós Graduação em Ciências Florestais a Universidade de Brasília (UnB). Email: marcobrunovaladao@gmail.com
7. Engenheiro Florestal pela Universidade de Brasília UnB. Email: joao.ncarrijo@gmail.com