

Vol. 38 (Nº 14) Año 2017. Pág. 15
Juliana de Castro REIS 1; Karina Thiebaut SACRAMENTO 2; João Carlos Correia Baptista SOARES DE MELLO 3; Lidia ANGULO MEZA 4
Recibido: 27/09/16 • Aprobado: 22/10/2016
3. DEA aplicado no setor ferroviário
6. Representação bidimensional da fronteira de eficiência
RESUMO: O objetivo deste estudo é avaliar a eficiência das ferrovias brasileiras no transporte de cargas, representadas pelas concessionárias responsáveis por fornecer este serviço, levando em consideração também a ação dos outputs indesejáveis desse processo. Devido ao grande número de variáveis, foi aplicado o Método Multicritério para Seleção de Variáveis. Com os resultados obtidos constatou-se que o método cumpriu o seu objetivo de manter uma eficiência média alta e uma boa discriminação das DMUs. A partir da representação gráfica bidimensional foi possível definir claramente a fronteira de eficiência e a localização de cada concessionária em relação a fronteira. |
ABSTRACT: The aim of this study is to evaluate the efficiency of Brazilian railways in cargo transportation, represented by the companies responsible for providing this service, taking into account also the action of undesirable outputs of this process. Due to the large number of pre-selected variables, the Multicriteria Method for Variable Selection was applied. The results suggest that the method has fulfilled its objective of maintaining an average high efficiency and good discrimination of DMUs. From the two-dimensional graphical representation it was possible to clearly define the efficient frontier and the location of each company in relation of this frontier. |
A indústria ferroviária ocupa um papel importante no mercado de fretes de cargas. Suas principais características são capacidade de transporte de grandes volumes de carga por longas distâncias, com baixo custo, segurança, níveis mais baixos de emissão de poluentes, e maior confiabilidade. Devido aos motivos destacados acima, pode-se afirmar que a ferrovia é de fundamental importância no transporte de cargas, em especial na cadeia produtiva do Brasil, que transporta em grande volume commodities minerais e agrícolas, produtos de baixo valor agregado, cujo frete de transporte impacta enormemente no preço final, e consequentemente, na competitividade dos mesmos no mercado internacional.
Entretanto, a matriz de transportes brasileira é fortemente dependente das rodovias, prejudicando o transporte e a exportação de cargas. Segundo dados do Ministério do Transporte (2012), 52% das cargas transportadas no país vão via modo rodoviário, e apenas 30% via ferroviário. Se considerarmos essa matriz de transporte sem o minério de ferro, principal utilizador das ferrovias, esta diferença fica ainda mais discrepante, sendo 68% via modo rodoviário, e apenas 10% via ferroviário.
As 12 malhas ferroviárias que compõem os principais trechos do sistema ferroviário nacional correspondem a 28.176 km de linhas férreas, e atendem às Regiões Sul, Sudeste, Nordeste e, em menor proporção, Centro-Oeste e Norte do País. Segundo a CNT (2011), o transporte ferroviário brasileiro registrou significativo crescimento desde o início das concessões à iniciativa privada. Nas duas últimas décadas, houve considerável aumento do volume de produtos transportados e da produção ferroviária, além de melhorias na segurança e na qualidade do serviço. A pesquisa ressalta ainda que, um dos caminhos para o Brasil retomar o desenvolvimento socioeconômico e permitir maior integração nacional é a priorização do transporte ferroviário, que levará ao equilíbrio da matriz de transporte de cargas e à consequente redução dos custos logísticos.
Visando ampliar a malha ferroviária brasileira e melhorar a qualidade e o custo do transporte de cargas no país, o Governo Federal lançou alguns programas de incentivo a melhoria da infraestrutura nacional, dentre os quais podemos destacas: PAC II (Programa de Aceleração do Crescimento II), o PNLT (Plano Nacional de Logística de Transporte), e mais recentemente o PIL (Programa de Investimentos em Logística), cujos objetivos são, principalmente, a expansão da malha ferroviária, de modo a permitir a ligação das áreas de produção agrícola e mineral a portos, indústrias e mercado consumidor, aumento da capacidade da malha atual e integração multimodal.
Esses novos trechos de malha ferroviária poderão ser concessionados, assim como grande parte da malha ferroviária atualmente existente, pois o sistema de concessão permite alavancar recursos e fazer os investimentos necessários para a melhoria do sistema. Baseado nisso, o presente estudo visa avaliar a eficiência das concessionárias atuais nos anos de 2011 a 2013, identificando quais seriam as mais eficientes para administração destes novos trechos, que até 2023 somariam 11 mil km à malha ferroviária do país (Ministério do Planejamento, 2012). Para análise desta eficiência é utilizado o modelo DEA BCC orientado a output, levando em consideração também a ação de outputs indesejáveis do processo.
O estudo está organizado da seguinte forma: na seção 2 é feita uma revisão dos modelos DEA clássicos e sua aplicação com outputs indesejáveis. A seção 3 faz uma revisão da literatura sobre a aplicação de DEA no setor ferroviário. Na seção 4 são apresentados o estudo de caso, a definição das variáveis e a aplicação do método. Na seção 5 encontram-se os resultados obtidos e, na seção 6 é apresentada a representação gráfica dos resultados. Finalmente, na seção 7 é feita uma conclusão para o estudo em questão.
DEA (Charnes et al, 1978) é uma abordagem não-paramétrica para análise de eficiência, baseada em modelos de programação matemática, cujo objetivo é calcular a eficiência de unidades produtivas (DMUs, do inglês Decision Making Units), que são otimizadas individualmente, comparando os recursos utilizados (inputs) e as quantidades produzidas (outputs) aos níveis de todas as outras DMUs.
Diferentemente das aproximações paramétricas, que otimizam um plano de regressão a partir das observações, o método DEA otimiza cada observação individual com o objetivo de calcular uma fronteira de eficiência, determinada pelas unidades que são Pareto eficientes, ou seja, que não conseguem melhorar alguma de suas características sem piorar as demais.
O resultado é a construção de uma superfície de envelope ou fronteira eficiente. As DMUs que se encontram na fronteira são consideradas eficientes (pontuação igual a 100%), e as demais ineficientes (pontuação inferior a 100%). Para cada DMU ineficiente, são calculados os alvos e um conjunto de referência. Os alvos de cada DMU ineficiente são os níveis de inputs ou outputs que devem ser alcançados para que as DMUs se tornem eficientes, enquanto o conjunto de referência representa as DMUs eficientes (benchmarks) que servem como exemplos de boas práticas de gestão.
Em geral, os modelos dispõem de formulações duais (envelope e multiplicadores), havendo duas orientações radiais possíveis: a inputs, que busca minimizar os recursos utilizados mantidos inalterados os níveis de produção; e a outputs, que implica no aumento da produção sem alterar as quantidades de insumos utilizadas.
Existem dois modelos DEA clássicos:
1) CCR (Charnes et al, 1978): também conhecido como CRS (Constant Returns to Scale), trabalha com retornos constantes de escala, ou seja, qualquer variação nas entradas produz variação proporcional nas saídas, obedecendo, portanto, a propriedade do raio ilimitado (Cooper et al, 2007). Esse modelo maximiza o quociente entre a combinação linear dos outputs e a combinação linear dos inputs, com a restrição de que para qualquer DMU esse quociente não pode ser maior que 1. O modelo CCR é apresentado em (1). Neste modelo Effo é a eficiência da DMU o em análise; vi e uj são os pesos de inputs i, i =1,...,r , e outputs j, j =1,...,s respectivamente; xik e jik são os inputs i e outputs j da DMU k, k =1,..., n; xio e yjo são os inputs i e outputs j da DMU o.
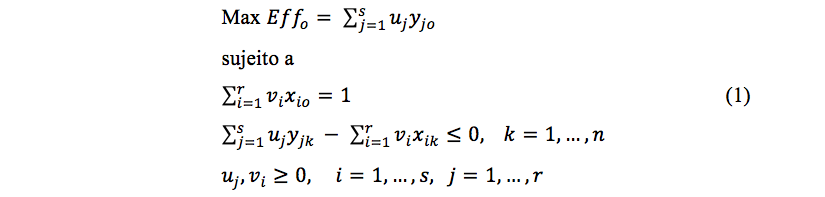
2) BCC (Banker et al, 1984): também conhecido como VRS (Variable Returns to Scale), que considera situações de eficiência de produção com variação de escala, substituindo o axioma da proporcionalidade entre inputs e outputs pelo da convexidade, e com isso deixando de obedecer, a propriedade do raio ilimitado. A formulação do modelo BCC usa para cada DMU o problema de programação linear (PPL) apresentado em (2). Nele, além das variáveis já apresentadas anteriormente, utiliza-se a variável u*, que é um é um fator de escala (quando positivo, indica que a DMU está em região de retornos decrescentes de escala; se negativo, os retornos de escala são crescentes; se nulo, a região é de retornos constantes de escala). No PPL (2), as variáveis de decisão são vi, uj e u*.
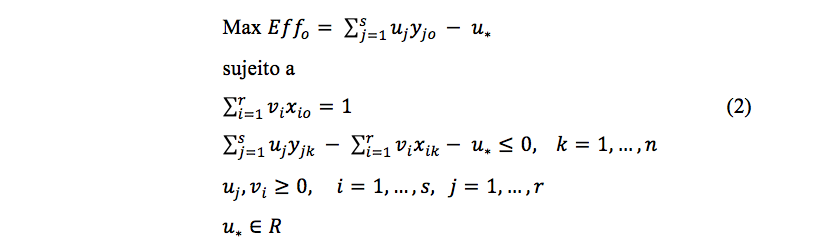
Em situações reais, como mencionado no trabalho de Koopmans (1951), o processo produtivo pode apresentar outputs indesejáveis, como poluição e desperdício. Ao avaliar o desempenho dos produtores faz sentido creditá-los pelas saídas desejáveis e sancioná-los pelas as saídas indesejáveis. Ou seja, "bens" e "males" devem ser tratados de forma assimétrica ao medir o desempenho do produtor.
Neste sentido, torna necessário prover o correto tratamento de tais variáveis para que a eficiência das unidades produtivas seja calculada da forma adequada. A seguir são apresentadas algumas abordagens que podem ser utilizadas na estruturação do modelo DEA para incorporar tais valores, como (Ângulo Meza e Tschaffon, 2011):
(1) Additive Inverse (ADD) – Neste método os outputs indesejáveis são transformados em outputs desejáveis através da troca de sinal dos valores dos outputs.
(2) Incorporating Undesirable Outputs and Inputs (INP) – Este método considera os outputs indesejáveis como inputs na estrutura do problema.
(3) Multiplicative Inverse (MLT) – Para incorporar outputs indesejáveis ao problema, estes são transformados em seu inverso. Entretanto, quando o output indesejável possuir valor zero, esta abordagem não pode ser usada.
(4) Translation (TRβ) – Esta alternativa de tratamento trata de transladar os valores, ou seja, significa adicionar à abordagem ADD um escalar positivo.
Scheel (2001) fez uma comparação destas quatro abordagens com o objetivo de verificar se os resultados das eficiências das DMUs permanecem os mesmos independentemente da abordagem utilizada. Os resultados mostraram que as eficiências das DMUs por ADD são preservados na abordagem por INP, assim como, se uma DMU é eficiente através da abordagem MLT então necessariamente permanecerá eficiente na abordagem ADD. Porém, uma DMU pode ser eficiente na abordagem ADD e não ser eficiente na abordagem MLT. Ou seja, a abordagem MLT é uma abordagem mais restritiva do que a ADD.
Atualmente, uma das abordagens muito utilizadas para o problema de DEA com outputs indesejáveis é a INP, como pode ser visto em Guo e Wu (2013), Li et al. (2013), Yang e Pollitt (2009), Hailu e Veeman (2001) e Korhonen e Luptacik (2004). Esta será a abordagem utilizada no presente estudo.
Devido à importância das ferrovias no desenvolvimento econômico de um país, o montante investido tanto pelo setor privado quanto pelo setor público vem crescendo exponencialmente nos últimos tempos. Por este motivo, estudos envolvendo análise de eficiência no transporte ferroviário vem sendo cada vez mais apresentados na literatura.
Yu (2008) utilizou os modelos DEA, TDEA (Traditional Data Development Analysis) e NDEA (Network Data Development Analysis) para comparar a eficiência de 40 ferrovias no ano de 2012. Os inputs utilizados foram comprimento da linha, número de funcionários, número de vagões de carga e número de vagões de passageiros, e como outputs foram utilizados tonelada por quilômetro e passageiros por quilômetro.
Himola (2010) apresenta em seu artigo o modelo DEA multi-estágio para analisar a eficiência operacional e financeira do modo ferroviário dos países. Para eficiência operacional, os inputs utilizados foram a quilometragem da malha, o número de vagões, de locomotivas e o número de funcionários, e os outputs considerados foram a tonelada quilômetro útil (tku) e a tonelada útil tracionada (tu). Já a eficiência financeira foi calculada utilizando como inputs, os outputs da modelagem da eficiência operacional (tku e tu) e como outputs a receita e o frete.
Caldas et al (2012) aplicam o modelo DEA CCR orientado a output para comparar a eficiência operacional das concessionárias brasileiras e americanas. Os inputs utilizados foram extensão da linha em quilômetros e número de funcionários utilizados para operar o trecho, e o output foi a quantidade de carga transportada no trecho (em toneladas).
Kutlar et al (2013) mediram a eficiência de 31 ferrovias de diversos países, de 2000 a 2009. Foram considerados como inputs o número de funcionários, comprimento da linha, número de vagões de carga, número de vagões de passageiros, número de veículos de operação e custa da operação anual. O estudo considerou como outputs tonelada por quilômetro, passageiros por quilômetro, tonelada transportada, número de passageiros transportados e receita anual.
Pereira e Soares de Mello (2014) estudam a eficiência das concessionárias brasileiras nos anos de 2009 a 2011, através do modelo DEA BCC orientado a output. Os inputs utilizados foram a meta de carga transportada (em bilhões de TKUs) e a extensão da malha concessionada, enquanto que os outputs foram a carga real transportada (TKUs) e a receita.
Pereira et al. (2015) analisam a eficiência das empresas concessionárias da malha ferroviária brasileira, no período de 2009 a 2013. Nesta análise são utilizados como inputs: área de concessão, número de empregados, gastos com pessoal, gastos com depreciação, outros gastos e total de gastos, bem como a receita líquida é utilizada como output.
Na literatura DEA, a grande maioria dos trabalhos publicados traz a abordagem da seleção de variáveis segundo a opinião de especialistas ou até mesmo da disponibilidade de dados (Senra et al., 2007). Observa-se que, em geral, não há uma preocupação em avaliar ou justificar o processo de escolha das variáveis.
Segundo Lins e Angulo Meza (2000), na maioria dos casos reais em que se dispõe de poucas variáveis e muitas DMUs, não se justifica a preocupação em utilizar técnicas de seleção em variáveis. Neste caso, o uso de todas as variáveis não deve trazer grandes desvantagens. Por outro lado, caso o número de DMUs seja pequeno, utilizar muitas variáveis pode diminuir o poder de discriminação do modelo e colocar grande parte das DMUs na fronteira de eficiência. Uma alternativa seria utilizar modelos avançados em DEA, ou ainda, tentar aumentar o número de DMUs a serem avaliadas. Se não for possível ou conveniente aos pesquisadores, uma solução seria restringir as variáveis que farão parte do modelo, fazendo uso de um dos métodos de seleção de variáveis, a fim de garantir que apenas os inputs e os outputs mais adequados sejam utilizados na avaliação de eficiência.
Neste artigo optou-se por utilizar o Método Multicritério para Seleção de Variáveis em Modelos DEA, proposto por Soares de Mello et al. (2002). A grande vantagem desse método é que combina uma boa relação causal entre inputs e outputs e uma boa discriminação entre as DMUs. Para implementar o método deve-se seguir os passos descritos abaixo.
1. Escolher um par input-output inicial. O decisor deve identificar qual o melhor par para iniciar a análise, considerando o tipo de avaliação de eficiência que pretende realizar;
2. Acrescentar uma nova variável ao modelo. De posse do par inicial, deve-se rodar o modelo DEA escolhido, acrescentando uma nova variável. Neste passo, o modelo será rodado uma vez para cada nova variável que ainda não foi incluída;
3. Calcular a eficiência média para cada variável acrescentada. Para cada resultado do passo anterior, calcula-se a eficiência média. Os valores obtidos das eficiências médias serão normalizados com o uso de uma interpolação que atribua valor 1 à maior eficiência média e 0 à menor. Este valor normalizado é chamado SEF.
4. Contar o número de DMUs na fronteira para variável acrescentada. Para cada resultado do passo 2 deve-se contar o número de DMUs consideradas eficientes. Este número será normalizado com o uso de uma interpolação invertida, que atribua valor 1 ao menor número de DMUs na fronteira e 0 ao maior número, e será chamado de SDIS. Dessa forma, quanto maior for o número de DMUs na fronteira menor será o poder discriminatório do modelo;
5. Calcular o valor de S, onde S = αSEF + (1 - α)SDIS. Neste ponto, cabe ao decisor escolher o peso de cada variável, para atribuir maior ou menor importância a cada um dos objetivos (aumentar a eficiência média e aumentar o poder de discriminação do modelo);
6. Escolher a variável que tenha maior valor de S para ser incluída no modelo. A alternativa que tiver o maior valor de S é considerada a alternativa que melhor concilia uma boa ordenação (alto valor de SDIS) e uma boa relação causal (alto valor de SEF);
7. Verificar se foi atingido o ponto de parada. Caso afirmativo deve-se encerrar a seleção de variáveis. Caso contrário, deve-se reiniciar o processo na etapa 2 incluindo mais uma nova variável no modelo. O ponto de parada deve ser deixado a critério do decisor. A Figura 1 representa de forma simplificada o processo descrito.
Figura 1: Método Multicritério para Seleção de Variáveis

Fonte: Elaborado pelos autores
No presente trabalho foram utilizados dados dos anos de 2011 a 2013 das concessionárias brasileiras de ferrovias, obtidos no site da ANTT - Agência Nacional de Transportes Terrestres, através de seus relatórios “Evolução do Transporte Ferroviário de Cargas”, publicado em 2016, e “Acompanhamento das concessões ferroviárias – Relatório Anual”, referente aos anos de 2011 e 2013.
Em um primeiro momento, foi realizado um levantamento de todas as possíveis variáveis para a avaliação da eficiência de ferrovias, que passaram por uma análise prévia para identificar quais deveriam ser consideradas inputs ou outputs e, ainda, quais dados estavam disponíveis.
Como inputs foram pré-selecionadas as variáveis: extensão da malha, em quilômetros; frota total de vagões e de locomotivas, que equivale ao número médio de vagões (ou locomotivas) disponíveis por ano; quantitativo de mão-de-obra, incluindo pessoal próprio e terceirizado; custo operacional, em milhares de reais; e investimento total, em milhões de reais.
Os outputs pré-selecionadas foram: carga transportada, em milhões de TKU, onde TKU equivale ao transporte de uma tonelada útil a distância de um quilômetro; receita líquida, em milhares de reais; e número de clientes. E como outputs indesejáveis foram pré-selecionadas: número de acidentes ferroviários, que são aqueles com a participação direta de veículo ferroviário; número de acidentes graves; e número de vítimas em acidentes ferroviários.
Em relação ao tratamento dos outputs indesejáveis, optou-se pela abordagem conhecida como INP (Incorporating Undesirable Outputs and Inputs), que considera os outputs indesejáveis como inputs, de forma a possibilitar a utilização de um modelo DEA clássico.
Observou-se que algumas variáveis apresentaram valor zero em determinados anos e, como variáveis com valor zero podem trazer prejuízos para o modelo e gerar enganos nos resultados da avaliação de eficiência, uma solução encontrada foi somar os dados dos três anos de cada concessionária. Os dados utilizados neste estudo são apresentados na Tabela 1.
Tabela 1: Dados das concessionárias somando os anos de 2011 a 2013
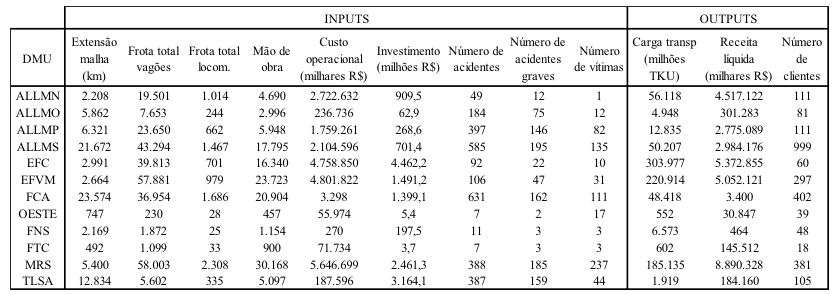
Fonte: Elaborado pelos autores
Neste estudo, o objetivo é avaliar a eficiência das ferrovias brasileiras no transporte de cargas, representadas pelas concessionárias responsáveis por fornecer este serviço no país, levando em consideração também a ação dos outputs indesejáveis desse processo.
Apesar das concessionárias operarem no mesmo ambiente de negócios e estarem sujeitas às mesmas normas de regulação, as características geográficas das regiões onde atuam e os produtos que transportam são muito diferentes, o que justificou a utilização do modelo BCC.
O modelo foi orientado a output, isto significa que deseja-se avaliar quanto as concessionárias poderiam estar produzindo dados os recursos que dispõem. Além disso, não faz sentido uma avaliação que vise minimizar determinados inputs, como por exemplo, a extensão da malha ferroviária sob concessão da empresa.
Como apresentado na Tabela 1, tem-se 12 concessionárias a serem avaliadas em um conjunto inicial de 12 variáveis pré-selecionadas. Por isso, optou-se por utilizar o Método Multicritério para Seleção de Variáveis, a fim de identificar as variáveis mais relevantes para o cálculo da eficiência. Este método permite que o decisor imponha uma certa direção ao modelo, o que se mostrou necessário para atingir o objetivo deste estudo de considerar os outputs indesejáveis.
No primeiro passo, foi escolhido o par “Número de acidentes - Carga transportada” como variáveis iniciais. Assim, garante-se que pelo menos um output indesejável (Número de acidentes) será incluído no modelo. No passo 2, o modelo DEA foi rodado repetidas vezes, com este par inicial e uma nova variável, para avaliar a inclusão de cada uma das outras dez variáveis. Em seguida, foram calculados os valores de SEF, SDIS e S como estabelece os passos 3, 4 e 5. Foi considerado que a relação causal entre inputs e outputs e a discriminação entre as DMUs tem o mesmo peso para este estudo. Logo, no cálculo de S, α = (1 - α) = 0,5. Os valores obtidos podem ser vistos na Tabela 2.
Tabela 2: Resultados da avaliação com a inclusão da terceira variável
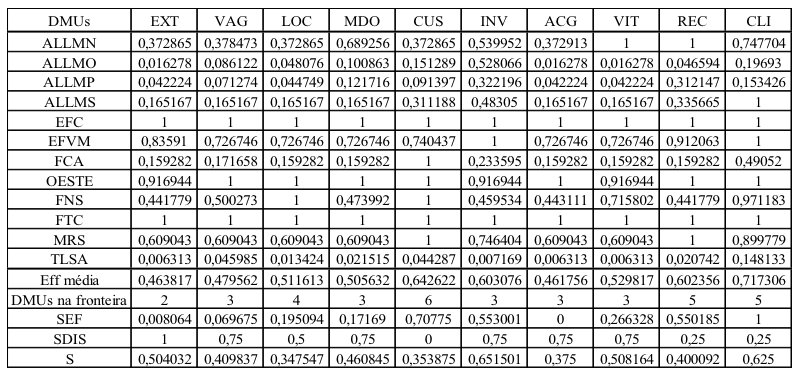
Fonte: Elaborado pelos autores
Observa-se que a inclusão da variável “Investimento” foi a alternativa que gerou um maior valor de S, 0,651501. Logo, esta é a variável que melhor concilia uma boa ordenação (alto valor de SDIS) e uma boa relação causal (alto valor de SEF) e, por isso será acrescentada ao modelo.
Para este estudo, foi determinado que o ponto de parada seguirá a Golden Rule estabelecida por Banker et al. (1989), que diz que o número de DMU’s deve ser igual ou maior a três vezes a soma total do número de variáveis. Então, como o ponto de parada ainda não foi atingido, deve-se voltar ao passo 2 e analisar qual será a próxima variável a entrar no modelo.
De forma análoga, o modelo foi rodado repetidas vezes, agora com dois inputs (“Número de acidentes” e “Investimento”) e um output (“Carga transportada”), acrescentando uma nova variável, para avaliar a inclusão de cada uma das outras nove variáveis que ainda restaram. E, em seguida, foram calculados os valores de SEF, SDIS e S. O resultado dessa nova iteração está apresentado na Tabela 3.
Tabela 3: Resultados da avaliação com a inclusão da quarta variável
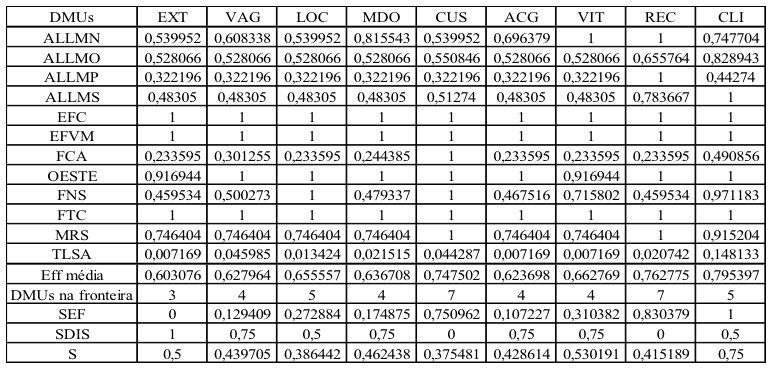
Fonte: Elaborado pelos autores
Nesta etapa, a variável (output) “Número de cliente” foi a alternativa que gerou um maior valor de S (0,75) e, portanto, esta foi a variável escolhida para ser incluída no modelo. Nota-se que neste momento, o ponto de parada foi atingido, pois tem-se 4 variáveis para 12 DMUs, exatamente o triplo do número de variáveis. Logo, chegou-se ao fim do método.
Com o Método Multicritério de Seleção de variáveis, foram selecionadas 4 variáveis para a avaliação de eficiência das concessionárias. Como inputs foram escolhidos “Investimento” e “Número de acidentes” e, como outputs, “Carga transportada” e “Número de clientes”.
Ao analisar as variáveis selecionadas, percebe-se que a definição do input “Investimento” foi bastante apropriada. Esta variável tem relação direta com muitos dos outros inputs, como por exemplo, a frota vagões e de locomotivas e quantitativo de mão-de-obra, já que o valor investido por uma concessionária é, direta ou indiretamente, revertido em melhorias nesses aspectos. Esta correspondência pode justificar a escolha do input “Investimento”, em detrimento desses outros citados.
O outro input utilizado, “Número de acidentes”, foi escolhido como par inicial juntamente com o output “Carga transportada”, com o intuito de atender ao objetivo do estudo e ter ao menos um output indesejável inserido no modelo. Já o output “Carga transportada” foi escolhido por ser a principal medida de produção ferroviária.
Por fim, o output “Número de clientes” também se mostrou adequado para a avaliação de eficiência, isso porque quanto menos clientes uma companhia tem, mais dependente desses clientes ela é. Assim, o objetivo também deve ser maximizar o número de clientes, visando aumentar a flexibilidade e lucratividade da empresa.
A partir da Tabela 4 é possível analisar os resultados finais da avaliação de eficiência das concessionárias.
Tabela 4: Resultados finais da avaliação de eficiência
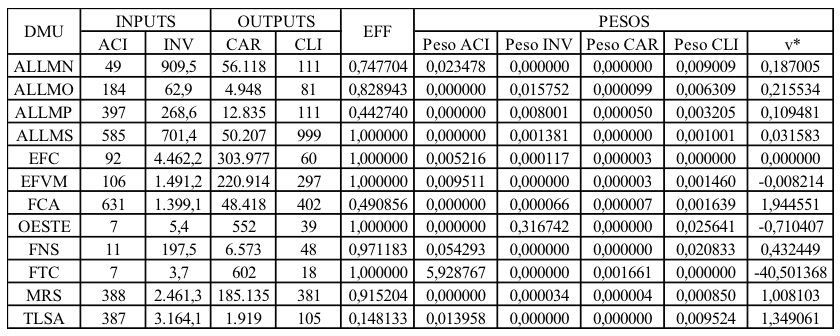
Fonte: Elaborado pelos autores
Cinco DMUs foram consideradas eficientes, ou seja, apresentaram índice de eficiência igual a 1. São elas: ALLMS, EFC, EFVM, OESTE e FTC. Com exceção da ALLMS, todas essas DMUs são verdadeiramente eficientes, pois no modelo CCR também obtiveram índice de eficiência igual a um. A DMU ALLMS é eficiente por ser a concessionária com o maior número de clientes, é uma eficiente por default do modelo BBC.
O conjunto de concessionárias eficientes é bastante heterogêneo, sendo formado por ferrovias de diferentes regiões do Brasil, com tamanhos de bitola divergentes, que transportam tipos de produtos distintos, não havendo como tirar qualquer conclusão sobre o porquê e quais fatores influenciaram para serem eficientes.
Por outro lado, a concessionária considerada menos eficiente foi a TLSA, com índice de eficiência de 0,148133. Nota-se que, em geral, as DMUs consideradas mais ineficientes, TLSA, ALLMP e FCA, respectivamente, estão entre as que apresentam o maior número de acidentes e de acidentes graves.
Bana e Costa et al. (2016) propuseram uma nova abordagem para representação bidimensional da fronteira de eficiência que pode ser utilizada nos casos com múltiplos inputs e múltiplos outputs, utilizando o input virtual e o output virtual para plotar as DMUs no gráfico. Para tal, tiveram que introduzir uma nova restrição de normalização, uma vez que nos modelos DEA clássico, a restrição adicionada para linearizar o modelo define, por exemplo, que o input virtual seja igual a 1 no modelo orientado a input. Dessa forma, em uma representação input virtual x output virtual, todas as DMUs estariam localizadas em uma mesma linha vertical, tornando o gráfico sem sentido.
Essa nova restrição utilizada por Bana e Costa et al. (2016) estabelece que a soma total dos pesos de todos os inputs seja igual a 1, transformando o modelo CCR orientado a inputs no modelo apresentado na equação (3).
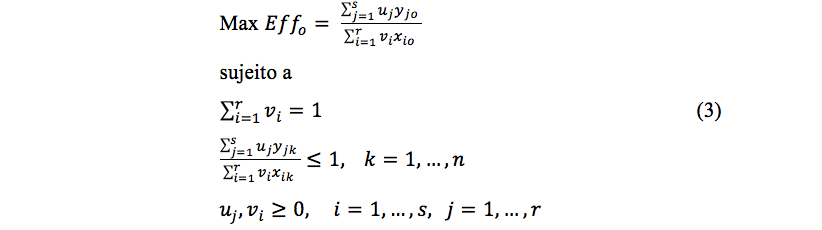
Para não utilizar essa nova formulação, que é um problema de programação fracionária, pode-se utilizar os resultados do modelo CCR linearizado (1) para calcular o novo input virtual modificado e o output virtual modificado.
Seja Sk a soma total dos pesos de todos os inputs da DMU k (4), calcula-se v’ik, o peso modificado do input i para a DMU k, e u’jk, o peso modificado do output j para a DMU k, utilizando as equações (5) e (6).

Os valores encontrados de I’k e O’k são utilizados para representar qualquer DMU k em um gráfico bidimensional. Nessa representação, a nova normalização torna a fronteira de eficiência uma linha reta que parte da origem e dividi o quadrante em duas seções iguais. Isto porque para uma DMU ser eficiente, seu input virtual modificado deve ser igual ao seu output virtual modificado (I’k=O’k).
Como o input e o output virtual modificado são divididos pelo mesmo número positivo, Bana e Costa et al. (2016) ainda comprovaram que o índice de eficiência não é afetado pelas manipulações algébricas realizadas, ou seja, a eficiência obtida pelo modelo modificado (3) é a mesma obtida pelo modelo CCR clássico (1).
Bana e Costa et al. (2016) também estenderam o seu modelo modificado para representação bidimensional para os casos de orientação a output e para os casos de retornos variáveis de escala (modelo BCC).
Como anteriormente neste estudo foi utilizado o modelo BCC orientado a output para calcular a eficiência das concessionárias de transporte ferroviário, o passo a passo descrito abaixo, também proposto no trabalho de Bana e Costa et al. (2016), foi utilizado para construir a representação gráfica bidimensional, respeitando as alterações necessárias devido ao modelo escolhido.

Os resultados dos passos 2, 3 e 4 podem ser observados na Tabela 5. E, a partir dos passos 5 e 6 foi construída a Figura 2, que representa a fronteira de eficiência e a localização de cada DMU.
Tabela 5: Pesos normalizados, input virtual modificado e output virtual modificado
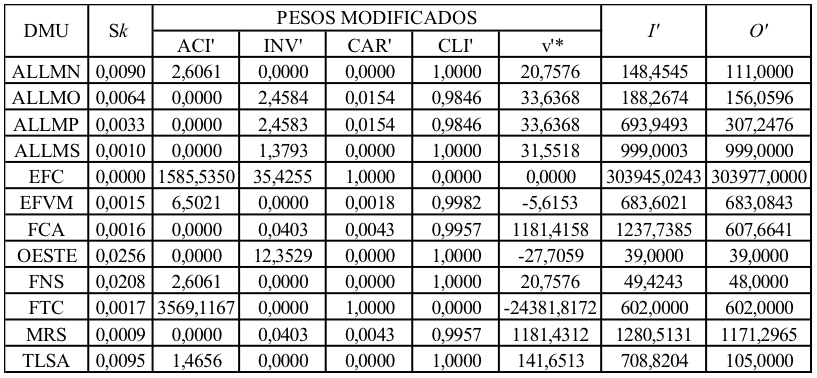
Fonte: Elaborado pelos autores
Figura 2: Representação bidimensional das concessionárias de serviço ferroviário
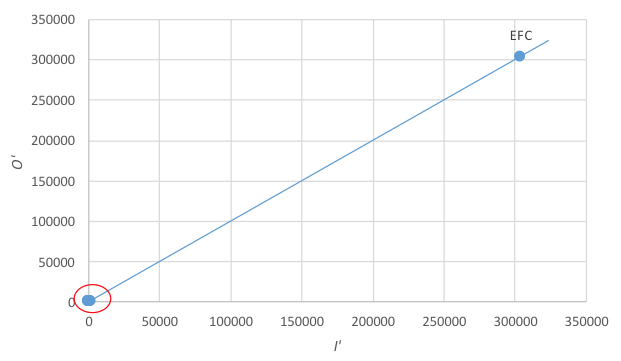
Fonte: Elaborado pelos autores
Nota-se que, por conta das diferenças de escala, há um grande número de DMUs concentradas perto da origem (0,0). Na verdade, apenas a concessionária EFC não se encontra nessa região. Para melhor visualizar as DMUs, a região circulada de vermelho na Figura 2 foi ampliada e está apresentada na Figura 3.
Figura 3: Ampliação da representação bidimensional das DMUs próximas a origem
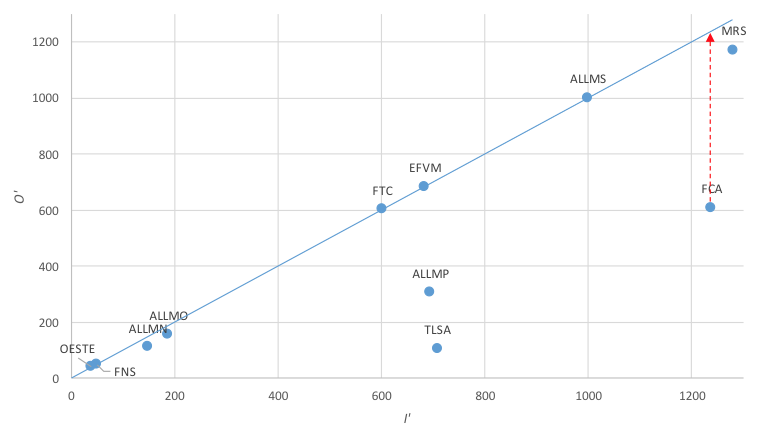
Fonte: Elaborado pelos autores
As DMUs localizadas sobre a bissetriz do gráfico representam as concessionárias consideradas eficientes, e abaixo dessa linha estão as DMUs ineficientes. A distância da DMU até a fronteira fornece uma ideia do quão ineficiente a DMU é; quanto mais distante da fronteira, mais ineficiente.
Observa-se que as DMUs estão concentradas bem próximas à fronteira eficiente, o que pode ser explicado pela característica do Método Multicritério de Seleção de Variáveis utilizado, que tem como um de seus objetivos a maximização da eficiência média do modelo.
Analisando a Figura 3 também é possível identificar os alvos de cada DMU, ou seja, o nível de output que precisa produzir para se tornar eficiente, já que o modelo é orientado a outputs. Neste caso, o alvo para o output virtual de cada DMU ineficiente é dado por um movimento vertical em direção à fronteira, como exemplificado pela seta vermelha no caso da concessionária FCA na Figura 3.
Neste estudo, o Método Multicritério para Seleção de Variáveis foi aplicado para auxiliar na decisão da escolha das variáveis mais adequadas para avaliação de eficiência das concessionárias de transporte ferroviário no Brasil. Foram selecionadas quatro variáveis, dois inputs “Investimento” e “Número de acidentes”, que na verdade é um output indesejável, e dois outputs, “Carga transportada” e “Número de clientes”.
Verificou-se que o método cumpriu o seu objetivo de manter uma eficiência média relativamente alta (0,795) com boa discriminação. Além disso, em geral as eficiências individuais foram altas, com exceção de apenas três DMUs, TLSA, ALLMP e FCA. Em relação ao poder de discriminação, apenas 5 DMUs encontram-se na fronteira de eficiência: ALLMS, EFC, EFVM, OESTE e FTC.
No entanto, ao analisar o conjunto de concessionárias eficientes, observa-se que este é bastante heterogêneo. Sendo formado por ferrovias de diferentes regiões do Brasil, com tamanhos de bitola divergentes, que transportam tipos de produtos distintos, não foi possível chegar a uma conclusão sobre o porquê e quais fatores influenciaram para alcançarem a eficiência. Pode-se apenas dizer que essas concessionárias são eficientes devido a aspectos gerenciais e administrativos, e não por questões ambientais.
Em relação a decisão de utilizar o Método Multicritério para Seleção de Variáveis pode-se afirmar que trouxe algumas vantagens para o modelo, como:
1. Propiciar uma eficiência média relativamente alta com boa capacidade discriminatória;
2. Possibilitar a incorporação da opinião do decisor na escolha do par inicial, de maneira a garantir que o objetivo de levar em consideração outputs indesejáveis na avaliação fosse cumprido.
A partir da representação bidimensional foi possível definir claramente a fronteira de eficiência e a localização de cada concessionária em relação a fronteira. A análise do gráfico reafirmou o cumprimento dos objetivos do método de seleção de variáveis utilizado, mostrando que as DMUs estão bem próximas à fronteira eficiente, sendo esta constituída por um número pequeno de DMUs.
Ângulo Meza, L., e Tschaffon, P. B. (2011). Um Estudo de Outputs Indesejáveis em DEA com Aplicação no Setor de Distribuição de Energia Elétrica. XLIII Simpósio Brasileiro de Pesquisa Operacional, SBPO, Ubatuba.
ANTT – Agência Nacional do Transporte Terrestre. (2013). Acompanhamento das concessões ferroviárias – Relatório Anual. Disponível em: http://www.antt.gov.br/index.php/content/view/4994/Relatorios.html#lista (acesso em 07/07/2016)
ANTT – Agência Nacional do Transporte Terrestre. (2016). Evolução do transporte ferroviário de cargas. Disponível em: http://www.antt.gov.br/index.php/content/view/15884/Evolucao_do_Transporte_Ferroviario.html (acesso em 07/07/2016)
Bana e Costa, C. A., Soares de Mello, J. C. C. B., e Angulo Meza, L. (2016). A new approach to the bi-dimensional representation of the DEA efficient frontier with multiple inputs and outputs. European Journal of Operational Research 255, p. 175–186.
Banker, R.D., Charnes, A. e Cooper, W.W. (1984). Some models for estimating technical scale inefficiencies in data envelopment analysis. Management Science, v. 30, n. 9, p. 1078-1092.
Banker, R. D. et al. (1989) An introduction to data envelopment analysis with some of its models and their uses. Research in governmental and non-profit accounting, New York, v. 5. p. 125-163.
Caldas, M. A. F., Gabriele, P. D., Carvalhal, R. L, e Ramos, T. G. (2012). A Eficiência do Transporte Ferroviário de Cargas: Uma Análise do Brasil e dos Estados Unidos. Congresso Latino Ibero-americano de Investigación Operativa e Simpósio Brasileiro de Pesquisa Operacional, XVI CLAIO - XLIV SBPO, Rio de Janeiro.
Charnes, A., Cooper, W.W., e Rhodes, E. (1978). Measuring the efficiency of decision-making units. European Journal of Operational Research, v. 2, n. 6, p. 429-444.
CNT – Confederação Nacional do Transporte. (2011) Pesquisa CNT de Ferrovias 2011. Disponível em: <www.cnt.org.br/Imagens%20CNT/PDFs%20CNT/Pesquisa%20CNT%20de%20Ferrovias/Pesquisa%20CNT%20de%20Ferrovias%202011.zip> Acesso em: 08 de Novembro de 2014.
Cooper,W.W., Seiford, L.M., e Tone, K. (2007). Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software. Springer Science, New York.
Guo, D. e Wu, J. (2013). A complete ranking of DMUs with undesirable outputs using restrictions in DEA models. Mathematical and Computer Modelling, v. 58 n. 5-6, p. 1102–1109.
Hailu, A. e Veeman, T. S. (2001). Non-Parametric productivity analysis with undesirable outputs: an application to the Canadian pulp and paper industry. American Journal of Agricultural Economics, v.83, n.3, p. 805–816.
Himola, O. (2010). Building efficiency from bottom-up? Analysing global railway freight. International Jounal of Logistics Economics and Globalisation, v. 2, n. 2, p. 139-150.
Koopmans T. (1951). Activity analysis of production and allocation. John Wiley & Sons, New York.
Korhonen, P. J. e Luptacik, M. (2004). Eco-efficiency analysis of power plants: An extension of data envelopment analysis. European Journal of Operational Research, v. 154, n. 2, p. 437–446.
Kutlar. A., Kabasakal, A., e Sarikaya, M. (2013). Determination of the efficiency of the world railway companies by method of DEA and comparison of their efficiency by Tobit analysis. Quality & Quantity, v. 47, n. 6, p. 3575-3602.
Li, X. G., Yang, J., e Liu, X. J. (2013). Analysis of Beijing's environmental efficiency and related factors using a DEA model that considers undesirable outputs. Mathematical and Computer Modelling, v. 58, n. 5-6, p. 956-960.
Lins, M.P.E. e Angulo Meza, L. (2000). Análise Envoltória de Dados e perspectivas de integração no ambiente do Apoio à Decisão. Editora da COOPE/UFRJ, Rio de Janeiro.
Ministério do Planejamento (2012). Programa de Investimentos em Logística. Disponível em: < http://www.pac.gov.br/pub/up/relatorio/601553fda730f7f943dbeea51cadd538.pdf> Acesso em: 07 de Julho de 2016.
Ministério dos Transportes (2012). Projeto de Reavaliação de Estimativas e Metas do PNLT. Disponível em: < http://www.transportes.gov.br/images/2014/11/PNLT/2011.pdf > Acesso em: 07 de Julho de 2016.
Pereira, L. A. M., e Soares de Mello, J. C. C. B. (2014). Eficiência técnica das concessionárias ferroviárias nacionais usando Análise Envoltória de Dados. Relatórios de Pesquisa em Engenharia de Produção, v.14, n. A18, p. 246-256.
Pereira, M. A., Rosa, F. S., e Lunkes, R. J. (2015). Análise da eficiência ferroviária no Brasil nos anos entre 2009 a 2013. Transportes, v. 23, n. 2, p.56-63.
Scheel, H. (2001). Undesirable outputs in efficiency evaluations. European Journal of Operational Research, v.132, n.2, p. 400–410.
Senra, L.F.A.C., Nanci, L.C., Soares de Mello, J.C.C.B., e Angulo-Meza, L. (2007). Estudo sobre métodos de seleção de variáveis em DEA, Pesquisa Operacional, Vol 27, No 2, pp. 191-207.
Soares de Mello, J. C. C. B., Angulo-Meza, L., Gomes, E. G., e Biondi Neto, L. (2005). Curso de Análise de Envoltória de Dados. XXXVIII Simpósio Brasileiro de Pesquisa Operacional, SBPO, Gramado.
Soares de Mello, J.C.C.B., Gomes, E.G., Soares de Mello, M.H.C., e Lins, M.P.E. (2002). Método Multicritério para Seleção de Variáveis em Modelos DEA. Pesquisa Naval, 15, 55-66.
Yang, H., e Pollitt, M. (2009). Incorporating both undesirable outputs and uncontrollable variables into DEA: The performance of Chinese coal‐fired power plants. European Journal of Operational Research, v. 197, n. 3, p. 1095‐1105.
Yu, M. M. (2008). Assessing the technical efficiency, service effectiveness, and technical effectiveness of the world’s railways through NDEA analysis. Transportation Research Part A: Policy and Practice, v. 42, n. 10, p. 1283-1294.
1. Mestrado em Engenharia de Produção – Universidade Federal Fluminense. Email: juliana.dcreis@gmail.com
2. Doutorado em Engenharia de Produção – Universidade Federal Fluminense. Email: karinathiebaut@yahoo.com.br
3. Departamento de Engenharia de Produção – Universidade Federal Fluminense. Email: jccbsmello@id.uff.br
4. Departamento de Engenharia de Produção – Universidade Federal Fluminense. Email: idiaangulomeza@id.uff.br