

Vol. 38 (Nº 04) Año 2017. Pág. 26
Eduardo Ferraz MARTINS 1; Gilson Brito Alves LIMA 2; Annibal Parracho SANT’ANNA 3; Renato Albes da FONSECA 4; Pedro Maffia da SILVA 5; Luiz Octavio GAVIÃO 6
Recibido: 24/08/16 • Aprobado:24/09/2016
4. Discussion and analysis of results
ABSTRACT: The techniques of risk analysis help identify threats, issues and anomalies of the processes that may affect the health and safety of employees, the environment and product quality. In this article, we used a stochastic risk analysis, with Monte Carlo simulation applied to FMEA (Failure Mode and Effect Analysis). The Monte Carlo simulation provides the decision maker a range of plausible outcomes and the probabilities of occurrences of these results. Among the corroboration of the simulation applied to FMEA include: Graphical interface due to data generated by the simulation, sensitivity analysis to determine which variables most affect the outcome, scenario analysis and probabilistic outcomes. As support for this study, the @Risk software was used. |
RESUMEN: Las técnicas de análisis de riesgo ayudan a identificar las amenazas, problemas y anomalías de los procesos que puedan afectar la salud y seguridad de los empleados, el medio ambiente y la calidad del producto. En este artículo, utilizamos un análisis de riesgo estocástico, con simulación Monte Carlo aplicada al AMEF (análisis del efecto y modo de falla). La simulación Monte Carlo proporciona al responsable de una gama de resultados posibles y las probabilidades de ocurrencias de estos resultados. Entre la corroboración de la simulación aplicada para AMEF: interfaz gráfica debido a datos generados por la simulación, análisis de sensibilidad para determinar qué variables afectan más los resultados, análisis de escenarios y los resultados probabilísticos. Como soporte para este estudio, se utilizó el software @Risk. |
The techniques of risk analysis help identify threats, issues and anomalies of the processes that may affect the health and safety of employees, the environment and product quality. Sharma (2012) reported the importance of considering techniques: qualitative and quantitative to analyze risks.
Calixto (2006) highlights in his studies, some of the most commonly used techniques in the literature: FMEA, FMECA, HAZOP, HAZID and WHAT IF (Qualitative risk analysis); AQR, SIL and FTA (Quantitative risk analysis). Santos (2012) also emphasizes that there are different types of risk classification, however, it is important to adopt a clear policy for managing catastrophic and critical risks, and to keep under control the moderate risks.
In this article, we used a stochastic risk analysis, with Monte Carlo simulation applied to FMEA (Failure Mode and Effect Analysis). According to Fogliatto and Ribeiro (2009), the FMEA is a technique, which helps search for excellence in projects and processes. Sant'Anna (2012) emphasizes that the FMEA is a tool to reduce the probability of critical failures through analysis of potential failures and the development of improvement actions. Nevertheless, the deterministic analysis is limited and does not consider the variations present in the judgments of experts. The presence of uncertainty in subjective measurements is a frequent problem (Sant'Anna, 2012). Important to emphasize that some relevance information may be lost by considering only the most frequent value in the analysis of experts. The graphic interface is also of great relevance for data interpretation. These factors stimulate the study of new proposals, such as that being discussed in this article.
The Monte Carlo simulation provides the decision maker a range of plausible outcomes and the probabilities of occurrences of these results. Among the corroboration of the simulation applied to FMEA include: Graphical interface due to data generated by the simulation, sensitivity analysis to determine which variables most affect the outcome, scenario analysis and probabilistic outcomes. As support for this study, the @ Risk software was used.
In the face of an extremely challenging environment is highlighted the role of engineering and related areas in mathematical models that can add value to the topic of reliability. In this context, this article targets the use stochastic risk analysis along with Monte Carlo simulation applied to FMEA as a tool of studying the critical risks on an X device.
The research made for the development of this article has the premise of achieving the following results: (1) To identify the failure modes on the X device; (2) To consider the evaluation of expert: Severity, Occurrence and Frequency for each failure mode with the use of FMEA; (3) Reflect, beyond the most frequent values (mode) in value judgment, the different opinions of experts for each criterion and failure mode; (4) Provide the decision-maker a range of plausible outcomes and the probabilities of occurrences of those results; (5) And Generate graphical interface with the data generated by the simulation, with the possibility of sensitivity analysis and scenario analysis.
This article is divided into three phases: The first part covers the initial considerations and the theoretical frame of reference; The second highlights the modeling with stochastic risk analysis, where the Monte Carlo simulation is applied to FMEA with support of @Risk software; In the third part, the enforcement of modeling is performed, as proposed in a study of the mechanical failure modes of an X device and an analyzes is generated with the final considerations.
Pentti and Atte (2002) reports that the first documentation of the FMEA was with the MIL-P-1629 procedure in 1949 by the United States Army (US Defense Department, 1949). This procedure served as a model for the development of military standards MIL-STD-1629 and MIL-STD-1629A, detailing the FMEA.
The use of FMEA, is also highlighted in the 60's, in the development of the Apollo project, by reports prepared by the National Aeronautics and Space Administration (NASA). (Bertsche, 2008; Clarke, 2005; Johnson, & khan, 2003; Mcdermott, Mikulak, & Beauregard, 2009; Puente et al., 2002; Seyed-hosseini, Safaei, & Ssgharpour, 2006).
In the 70s, the theme about the tool started to be discussed more widely. And in 1978, Ford was the pioneer in the automotive industry to integrate FMEA in its concept of quality assurance (Clarke, 2005).
Following the initiative of Ford, in the 80s, the automobile companies that form the AIAG (Automotive Industry Action Group), formally incorporated the tool into their product development processes through the QS-9000 (Laurenti, Villari, & Rozenfeld, 2012).
Currently, the application of FMEA can be observed in different areas of interest: Medicine (Apkon, Leonard, Probst, Delizio, & Vitale, 2004; Cohen, Senders, & Davis, 1994; Derosier, Stalhandske, Bagian, & Nudell, 2002; Mcnally, Page, & Sunderland, 1997), in computer science (Yacoub, & Ammar, 2002; Yang, Bonsall, & Wang, 2008), chemical engineering (Cournoyer, Garcia, Gallegos, & Wilburn, 2011; Goyal, 1993; Wang, Cheng, Hu, & Wu, 2012); In the energy sector (Burgazzi, 2004; Garcia, Schirru, Frutuoso, & melo, 2005; Guimarães, & Lapa, 2004; Guimarães, & Lapa, 2007), among other sectors.
The FMEA begins with the identification of roles and requirements of a system, subsystem, component or step process (Bertsche, 2008). Followed by determining failure modes, effects and causes of each failure mode.
The next step is the value judgment of a multidisciplinary group, which assigns values (range 0-10), the effects of Severity (S), and the probability of occurrence (O) of the causes or their modes (AIAG, 2008). Afterwards, values (scale from 0 to 10) for the difficulty of detection (D) are assigned. At this stage, the current controls to prevent and detect the failure mode and / or causes are taken into account (Bertsche, 2008). The product of the values of S, O and D, known as Risk Priority number (RPN) according to equation 1, is considered.
RPN = (S) x (O) x (D)
Equation 1: Calculating the RPN
After value judgment, the group should propose actions to eliminate or detect failure modes, its causes and also reduce its effects (AIAG, 2008). Fogliatto and Ribeiro (2009) report that the recommended actions should be directed to the items with higher risk, with indication of the responsible and the deadline for implementation.
The FMEA was initially used with scales of 11 levels (US Military 1949, 1980). Over time, scales of five levels have been most used (Sant'Anna, 2010). The use of scale with five levels simplifies the analysis by the experts and has been used by different authors. For more information on the scales of five levels or studies with similar scales, see British Standards Institute (1991), Ben-Daya and Raouf (1993), Rosa and Garrafa (2009) and Nogueira and Perez (2010).
Fogliatto and Ribeiro (2009) points out that among the advantages of using FMEA in the literature, it includes:
• Assists in identifying the parameters to be controlled to reduce or detect a fault condition;
• Helps prioritize potential failure modes, establishing an order for improvement actions;
• Assists in the evaluation of alternatives for the manufacture or assembly, for example;
• Documents the results of the study, facilitating future analysis;
• Consolidates and increases knowledge of all involved for all aspects of the process associated with the quality and reliability of the product;
• It establishes a frame of reference that assists in analyzing and improving similar processes.
A method that has been applied to take uncertainty into account in FMEA consists of using fuzzy logic to compose the index, measured according to each criterion by fuzzy numbers (Sant'Anna, 2012). In this context, Sant'Anna (2012) combined the probabilistic composition with an experts’ global evaluation.
To deal with the imprecision and subjectivity in measurements, Fuzzy Sets Theory provides a simple basis to operate (Zadeh, 1965). The need to develop tools to deal with uncertainty in the assessments according to various criteria, is recognized in the development of methods for decision support like: ELECTRE (Roy, 1968), AHP (Saaty, 1980) and MACBETH (Bana e Costa and Vansnick, 1995).
The study structure consists of three phases and nine steps. The methodology is shown in Figure 1.
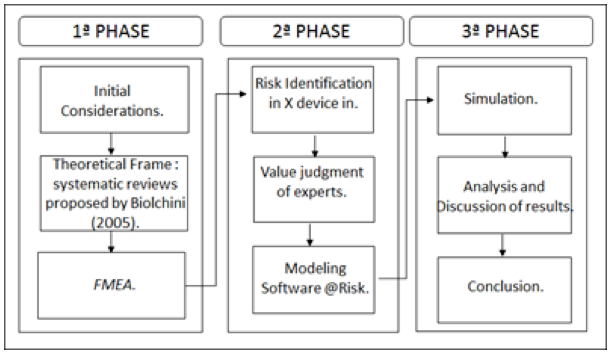
Figure 1: Structure of the study
For the article proposed in the first phase, initial considerations were conducted and a study of the theoretical frame of reference was elaborated, as seen on topic two. It was considered, for this study, a systematic review proposed by Biolchini (2005), which highlights three main steps: Planning, Execution and Analysis.
The following inputs of the traditional FMEA were identified on the theoretical frame of reference: Occurrence (O), detection (D) and Severity (S). And the output, represented by the Risk Priority Number (RPN), was also identified. The RPN is identified after the multiplication of the input factors according to equation 1.
After identifying the RPN for each failure mode, it was verified that it is possible to prioritize them. Important concepts such as the origin, applications and advantages of using the FMEA were also highlighted in this first approach.
In the second phase, the failure modes of the X device were identified and the value was determined, with the help of experts. The data that was used in this study of the X device is presented throughout the article, but will not be detailed for confidentiality reasons. Next, the modeling study was performed with the support of the software @Risk, which will be presented in the next section.
The third phase shows the Monte Carlo simulation applied to FMEA. The Monte Carlo simulation provides the decision maker a range of plausible outcomes and the probabilities of occurrences of those results.
In the final steps of the third phase, the results were discussed and the contribution of the Monte Carlo simulation, applied to analysis of failure mode and effect (FMEA), was highlighted.
It was applied to FMEA, in a study on the failure modes of the operation of an X device. It was identified: electrical and electromagnetic failure modes, mechanical failure modes, chemical failure modes, thermal failure modes. This study will be treated mechanical failure modes that are:
• M1 - Impact on guidance unit;
• M2 - Impact of flooding valve;
• M3 - Impact of the initiator;
• M4 - Impact of the X device section during movement in crane;
• M5 - Impact of equipment X device for handling the crane;
• M6 - Fall of the X device equipment on the transport vehicle;
• M7 - Fall of equipment X device on the crane.
After identifying the failure modes, the value judgment of 30 experts was conducted. It was assigned, for each failure mode, a value in the range 1-5, for the occurrence, severity and frequency.
In the severity criteria, the greater the scale value, the greater the risk of impact. Regarding occurrence, the frequency of risk is higher when the scale value approaches 5 and regarding risk detection, it becomes very difficult when the value judgment gets close to 5. The details of the scale and criteria of occurrence, severity and detection, is presented in Attachment 1.
The format of the applied questionnaire, which was answered by 30 specialists, can be observed in Attachment 2. And the values of judgment of the experts, the mode of each criteria (most frequent value) to respective risk, and RPN (s) of the traditional FMEA are in attachment 3.
The following figure illustrates the inputs and outputs for the Monte Carlo simulation. For the first identified failure mode (M1), we have the following criteria: Severity (S), frequency (F) and Occurrence (O), the extremes of the experts’ value judgment and the mode (most frequent value). The data will include the parameters of the triangular distribution. In the case of M1, in terms of severity (S), we have:
• a - Represents the value of the lowest value judgment present of the 30 experts;
• a`- Represents the most frequent value (mode) in the judgment of the experts;
• a`` - Represents the largest value in the judgment of the experts.
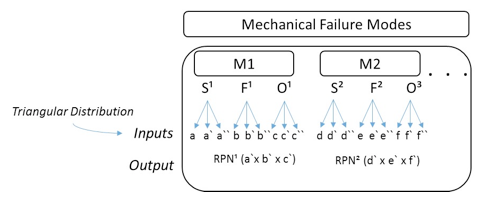
Figure 2: Monte Carlo Simulation applied to FMEA
It is observed that the model logic was first developed in a usual manner, that is, using basic Excel formulas. This logic can be seen in Figure 3, which was generated based on Attachment 3.
In Figure 3, the following values for each criteria (Severity, Occurrence and Detection) were assigned to each failure mode (M1, M2, M3, M4, M5, M6 and M7):
• Highest value judgment given by one or more experts;
• Lowest value judgment given by one or more experts;
• Most frequent value (Mode) given by experts;
• RPN(s) as a function of multiplying the most frequent value of S, O and D for each failure mode.
It is observed that the input values shown in Figure 3 are uncertain. When we analyze the severity of the failure mode M1, the input represented by the most frequent value (two), can vary from one to four. This occurs for the other criteria and failure modes identified. Thus, in the case of the severity criteria M1, these three values will compose the extremes and the central element of the triangular distribution. We will also have a triangular distribution for the occurrence of the M1 criteria represented by the parameters (1, 3 and 5) and the detection criteria (1, 2 and 3). In the language of @Risk, the M1 detection criteria would be represented by "RiskTriang (1; 2; 3; RiskStatic(2))." The same analysis should be performed to the other failure modes.
The variation of each criteria occurs because there is some subjectivity in value judgment that changes for each expert. It is understandable then, that considering this variability is important to avoid mistakes in analysis. It is also understandable that even a deterministic analysis is somewhat limited and may delete important data in the study.
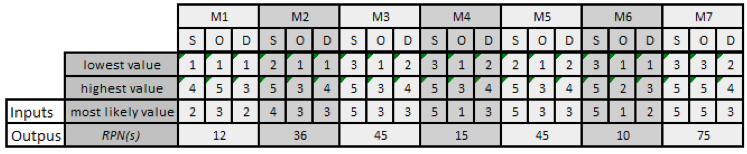
Figure 3: Logic Model
After this initial understanding, the number of 1000 interactions for the simulation was defined. This means that 1000 RPN(s) (outputs) will be generated for each failure mode considering random variations in inputs, which will follow a triangular distribution as explained above. After this stage, the data analysis is performed and will be discussed in the following section.
During a simulation analysis is important to consider the correlation between the input variables. Because otherwise the simulation can bring in meaningless data. In a high tech environment, for example in the case of a high severity is expected a high control of the failure mode and a low frequency. However this study took place in a relatively low-tech environment and for this reason the correlations were not observed in the presented study. With this the variables: Severity, Occurrence and Detection were treated independently.
In many respects, the triangular distribution is an ideal approach for soliciting an expert`s evidence when the expert is not comfortable with the assessment of probabilities (HAIMES,1998). Still according Haimes (2008) here the expert is not asked to assess probabilities. Rather, only three assessments of outcomes are solicited from the experts: lowest value, highest value, and most likely value. In this work the values: highest, benevolent and more frequent of experts value judgments are used to build scenarios and to analyze the criticality of each failure mode.
After the simulation, a multitude of analysis with support of @Risk can be made. Among some graphics that can be observed, we have: density of probability, discrete probability, cumulative ascending, descending and relative frequency. In the picture below, there is a representation of the simulation for M1 failure mode. It is observed that there is a 90% probability of the M1 RPN1 to be between 5.68 and 26.46. Thus, the probability of different RPN (s) for the risk M1 can be verified.
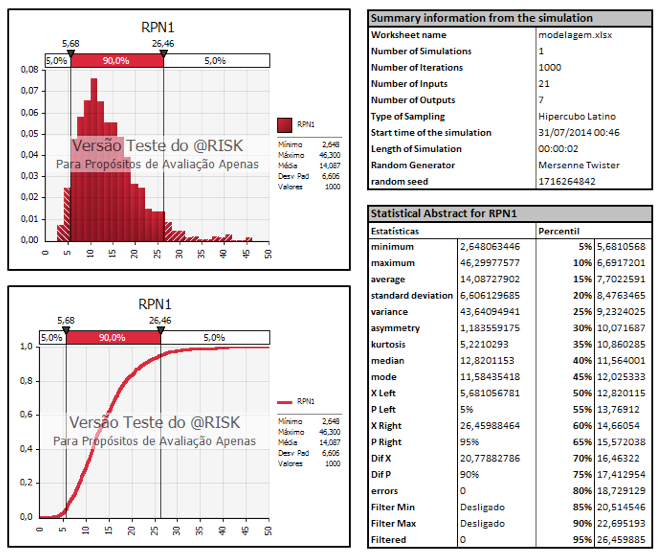
Figure 4: Probability Density (RPN1)
For the critical risk analysis (M1, M2, M3, M4, M5, M6 and M7), the interval with a probability of 90% chance of occurrence, was considered. Figure 5 shows this analysis with a summary of all risks.
• In the case of M2, for example, there is a 90% probability that the RPN2 is between 10.77 and 37.45;
• M3 90% probability of 17.09 ≤ RPN3≤ 44.08;
• M4 90% probability of 12.34 ≤ RPN4≤ 35.94;
• M5 90% probability of 14.45 ≤ RPN5≤ 42.27;
• M6 90% probability of 6.69 ≤ RPN6≤ 17.91;
• M7 90% probability of 38.79 ≤ RPN7≤ 77.01.
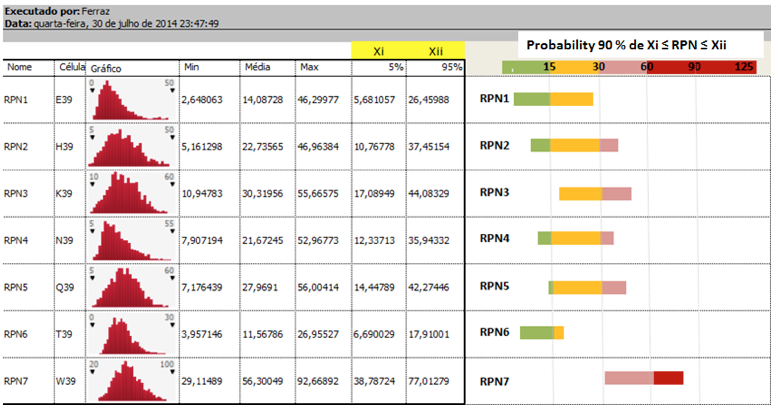
Figure 5: Probability Density of all risks
Figure 5 above, shows a bar graph representing the RPN (s) intervals previously mentioned, with a probability of 90% chance of occurrence. It is observed that the maximum RPN is 125 because each failure mode has three criterias (Severity, Frequency and Detection) respecting the scale with the maximum of five. The color of the bar changes as the increase in RPN and criticality of risk.
The M7 failure mode, stood out from the others presenting a range of critical RPN. Even at the minimum value, the risk M7 presents a high RPN and deserves immediate priority. The M6 failure mode presented values of RPN (s) relatively low, indicating that this risk can be observed without an immediate priority. failure modes M3, M5, M2 and M4, in descending order can reach high values of RPN, entering the red zone. Therefore, after the M7 in said order is interesting attention to these risks with a relative prioritization. These risks must be monitored with balanced attention since it can be reversed the prioritization depending on the value judgment of experts. A priority inversion can occur when carefully analyzing the 1000 interactions. That is, the variability of judgment may indicate that the vision of a certain risk specialist should be prioritized, and this analysis may be different from other professionals.
Finally, despite the variation, M1 failure mode does not enter the red zone, which indicates that just like the M6, this failure mode can be observed without an immediate need for prioritization.
It was also used in stochastic analysis another Distribution as the normal distribution that is present in attachment 4. For the use of the distribution were considered as inputs the average of each criterion for each failure mode and its standard deviation, since the judgment of experts. The results were consistent with the use of the triangular distribution. The modes of M7 and M3 failures were highlighted as most critical. And the M6 and M1 modes as less critical. For future studies it is suggested to use also other distributions besides the normal and triangular.
In traditional FMEA, after the multiplication of the most frequent values of occurrence, detection and severity are presented the following critical indices: M7 – 75; M5 – 45; M3 – 45; M2 – 36; M4 – 15; M1 – 12 e M6 – 10. In stochastic analysis beyond these values are considered other scenarios as the assessment more severe and more benevolent.
When the two results are compared there is a consistency that is observed, for example, in the case of M7, M5, M3 which are among the most critical failure modes. However, the stochastic analysis enables us to distinguish the case of M3 and M5, which have the same value in traditional analysis. In stochastic analysis is observed that in most benevolent scenario as the most severe, M3 has a higher criticality index. This allows you to check the level of attention that should be given to M3 and M5 in this case.
Other failure modes were consistent also as in M1 and M6 seen as less critical. However, the stochastic analysis shows the difference of the value judgments of experts. When M2 and M4 analysis is made, for example, although M2 presenting a higher critical value in traditional FMEA, depending on the value of a given expert judgment M2 can have a lower index than M4. And this is considered in stochastic analysis. With this type of analysis is understood that the attention to the two failure modes should be balanced, since it can occur change the criticality of order.
According to the results obtained in this study, the stochastic risk analysis with Monte Carlo simulation applied to FMEA, contributed for the decision maker to have a range of plausible outcomes and to have obtained the probabilities of occurrences of those results. It is also noted that it was considered intrinsic subjectivity in judgment of each expert with the proposed analysis.
The different value judgments were included, since their absence can be detrimental to the interpretation of data and information. For this, we used a triangular distribution to each failure mode, considering the central element (mode) and the extremes (highest and lowest value) of each criteria. In addition to these factors, Monte Carlo simulation allowed the simulation, 1000 interactions in this case, to consider the possible variations within the established limits.
The deterministic assessment may have some limitations, such as the study of scenarios and sensitivity. As approached on the topic of case analysis, it is observed that depending on the interaction studied, reversal of the priority of critical risks may occur. With the proposed study is possible to analyze the extremes and the probability of occurrence of intervals of criticality.
In the context of this work, it is evident the importance of engineering or related areas for modeling problems and for developing techniques to provide a safer environment.
This study allowed, beyond what has already been discussed, the following conclusions:
• It was possible to analyze the criticality of failure modes (M1, M2, M3, M4, M5, M6 and M7), considering the differences in value judgment by experts. That is, in addition to the most frequent value of each criteria, the extremes were also considered. The simulation with these parameters also considers that variations can occur within these limits and does not rule out information that may be important for the analysis. For example, the failure mode M4, presents in Figure 3 an RPN = 15, one of three smallest RPN’s. In Figure 5, the upper limit enters an area that deserves attention (relative prioritization). This analysis, based on variations of the limits, can be considered an insight.
• The deterministic analysis is limited. With the proposed analysis, is possible a more detailed analysis of different situations; In the deterministic analysis is complicated to model different combinations of values for different inputs.
• The graphical interface is important for communication and comparison of the results achieved; It can also be used for the assessment of probability of occurrence. Therefore, provide important insights that could go unnoticed;
• The results show what could happen and also shows the probability of occurance;
• Mechanical hazards presented on the X device were identified and these values were assigned based on expert judgment and criteria of severity, occurrence and detection. The different opinions of experts were contemplated, recognizing the importance of these differences for the study. The decision maker is equipped with a range of outcomes and the probabilities of occurrence of these results to analyze the priorities of critical risks. The graphical interface was created as a means to facilitate data interpretation.
AIAG. (2008). Potential Failure Mode and Effects Analysis (FMEA) - Reference Manual, 4th Ed.
Apkon, M., Leonard, J., Probst, L., Delizio, L., & Vitale, R. (2004). Design of a safer approach to intravenous drug infusions: Failure mode effects analysis. Quality and Safety in Health Care, 13 (4), pp. 265-271.
Bana e Costa, C. A., & Vansnick, J. (1995). “Uma nova abordagem ao problema da construção de uma função de valor cardinal: MACBETH”. Investigação Operacional, 15 (1), pp. 15-35.
Ben-daya, M., & Raouf, A. (1993). A revised failure mode and effect model. International Journal of Quality & Reliability Management, 13 (1), pp. 43-47.
Bertsche, B. (2008). Reliability in Automotive and Mechanical Engineering: Determination of Component and System Reliability. Berlin: Springer.
Biolchini, J., Mian, P. G., Natali, A. C. C.; & Travassos, G. H. (2005). Systematic Review in Software Engineering: Relevance and Utility. Rio de Janeiro: PESC-COPPE/UFRJ.
BRITISH STANDARDS INSTITUTE. (1991). BS5760: Reliability of Systems, Equipment and Components – Part 5. Guide to Failures Modes, Effects and Criticality Analysis (FMEA and FMECA).
Burgazzi, L. (2004). Evaluation of uncertainties related to passive systems performance. Nuclear Engineering and Design, 230 (1-3), pp. 93-106.
Calixto, E. (2006). Uma metodologia para gerenciamento de risco em empreendimentos: Um estudo de caso na Indústria de petróleo. Fortaleza: XXVI ENEGEP.
Clarke, C. (2005). Automotive Production Systems and Standardization: From Ford to the Case of Mercedes-Benz. Heidelberg: Physica-Verlag.
Cohen, M.R., Senders, J., & Davis, N. M. (1994). Failure mode and effects analysis: A novel approach to avoiding dangerous medication errors and accidents. Hospital Pharmacy, 29 (4), pp.319-330.
Cournoyer, M. E., Garcia, V. E., GALLEGOS, U. F., & WILBURN, D. W. (2011). Investigation of injury/illness data at a nuclear facility. Journal of Chemical Health and Safety, 18 (5), pp. 17-25.
Derosier, J., Stalhandske, E., Bagian, J. P., & Nudell, T. (2002). Using health care Failure Mode and Effect Analysis: the VA National Center for Patient Safety's prospective risk analysis system. The Joint Commission journal on quality improvement, 28 (5), pp. 248-267.
Fogliatto, F. S., & Ribeiro, J. L. D. (2009). Confiabilidade e Manutenção Industrial. (1st ed.). Porto Alegre: Elsevier.
Garcia, P. A. A., Schirru, R., Frutuoso, & Melo, P.F. (2005). A fuzzy data envelopment analysis approach for FMEA. Progress in Nuclear Energy, 46 (3-4), pp. 359-373.
Goyal, R. K. (1993). FMEA, the alternative process hazard method. Hydrocarbon Processing, 72 (5), pp. 95-99.
Guimarães, A. C. F., & Lapa, C. M. F. (2004). Fuzzy FMEA applied to PWR chemical and volume control system. Progress in Nuclear Energy, 44 (3), pp. 191-213.
Guimarães, A. C. F., & Lapa, C. M. F. (2007). Fuzzy inference to risk assessment on nuclear engineering systems. Applied Soft Computing Journal, 7 (1), pp. 17-28.
Haimes, Y.Y. (1998). Risk modeling, assessment, and management, Wiley, New York.
Johnson, K. G., & Khan, M. K. (2003). A study into the use of the process failure mode and effects analysis (PFMEA) in the automotive industry in the UK. Journal of Materials Processing Technology, 139 (1-3), pp. 348–356.
Laurenti, R., Villari, B. D., & Rozenfeld, H. (2012). Problemas e melhorias do método FMEA: uma revisão sistemática da literatura. Pesquisa & Desenvolvimento Engenharia de Produção 10 (1), pp. 59-70.
Mcdermott, R. E., Mikulak, R. J., & Beauregard, M. R. (2009). The Basics of FMEA. (2nd Ed.). New York: Productivity Press.
Mcnally, K. M., Page, M. A., & Sunderland, V. B. (1997). Failure-mode and effects analysis in improving a drug distribution system. American Journal of Health-System Pharmacy. 54 (2), pp. 171-177.
Nogueira, A. C., & Peres, A. P. (2010). Comparação entre duas matrizes FMEA aplicadas em Laticínios de Lavras-MG. Engenharia Ambiental, 7 (2), pp. 178-189.
Pentti, H., & Atte, H. (2002). Failure mode and effects analysis of software - based automation systems. STUK - Radiation and Nuclear Safety Authority. Helsinki.
Puente, J., Pino, R., Priore, P., & Fuente, D. D. L. (2002). A decision support system for applying failure mode and effects analysis. International Journal of Quality & Reliability Management, 19(2), pp.137-150.
Rosa, L. C., & Garrafa, M. (2009). Análise dos modos de falha e efeitos na otimização dos fatores de produção no cultivo agrícola: subprocesso colheita de canola. Gestão & Produção, 16 (1), pp. 63-73.
Roy, B. (1968). “Classement et choix en présence de points de vue multiples. Revue Française d’Automatique d´Informatique et de Recherche Opérationnelle, 8 (1), pp. 57-75.
Saaty, T. L. (1980). The Analytic Hierarchy Process. New York: McGraw-Hill.
Sant’Anna, A. P., Junior, R. P. S. P. (2010). Composição probabilística no cálculo das prioridades na FMEA. Revista Eletrônica Sistemas & Gestão, 5 (3), pp. 179-191.
Sant’Anna, A. P. (2012). Probabilistic priority numbers for failure modes and effects analysis. International Journal of Quality & Reliability Management, 29(3), pp. 349-362.
Santos M. A. (2012). Ferramenta de análise de riscos em projetos de capital considerando conceitos de confiabilidade humana e engenharia de resiliência. 2012. 114 f. Dissertação (Mestrado em Engenharia Ambiental) Programa de Pós-Graduação em Engenharia Ambiental, Escola Politécnica & Escola de Química, Universidade Federal do Rio de Janeiro, Rio de Janeiro.
Seyed-hosseini, S. M., Safaei, N., & Asgharpour, J. (2006). Reprioritization of failures in a system failure mode and effects analysis by decision making trial and evaluation laboratory technique". Reliability Engineering & System Safety, 91(8), pp. 872 – 881.
Sharma, R. K., Sharma P. (2012). Integrated framework to optimize RAM and cost decisions in a process plant. Journal of Loss Prevention in the Process Industries, 25 (6), pp. 883-904.
US Military. (1949). Procedures for Performing a Failure Mode, Effects and Criticality Analysis, United States Military Procedure MIL-P-1629.
US Military. (1980). Procedures for Performing a Failure Mode, Effects and Criticality Analysis, United States Military Procedure MIL-P-1629a, 1980.
Wang, Y., Cheng, G., Hu, H., & Wu, W. (2012). Development of a risk-based maintenance strategy using FMEA for a continuous catalytic reforming plant. Journal of Loss Prevention in the Process Industries, 25 (6), pp. 958-965.
Yacoub, S. M., & Ammar, H. H. (2002). A methodology for architecture-level reliability risk analysis. IEEE Transactions on Software Engineering, 28 (6), pp. 529-547.
Yang, Z., Bonsall, S., & Wang, J. (2008). Fuzzy rule-based Bayesian reasoning approach for prioritization of failures in FMEA. IEEE Transactions on Reliability, 57 (3), pp. 517-528.
Zadeh, L. A. (1965), “Fuzzy sets”, Information and Control, 8, pp. 338-53.
SEVERITY |
Description |
Points |
||
Personal Safety |
Facility Safety |
Environment |
||
VERY LOW |
No injuries, damage or alterations. |
No damage or negligible damage to equipment or facilities. |
No damage to the environment. |
1 |
LOW |
Minor lesions resolved in staff with small bandages or simple treatments, discrete changes. |
Slight damage to equipment or facilities. Controllable damage and / or low cost repair. |
Light impacts on the environment and reversible with immediate actions. |
2 |
MODERATE |
Moderate injuries in employees who need care. |
Damage to equipment or facilities that cause degradation in system performance. |
Localized and reversible moderate impacts with mitigation actions. |
3 |
HIGH |
Disabling injury not serious or permanent occupational disease. |
Severe damage to equipment or facilities. High cost of repair. |
Severe and reversible impacts with mitigation actions. |
4 |
VERY HIGH |
Permanent disabling injury, severe occupational illness or likelihood of death. |
Irreparable damage to equipment or facilities. Repairing impossible. |
Catastrophic and irreversible impacts even with mitigating actions or requiring high external resources. |
5 |
OCCURRENCE |
Description |
Points |
||
VERY IMPROBABLE |
Scenario depends on multiple failures of the protection system. Conceptually possible, but extremely unlikely to occur. |
1 |
||
IMPROBABLE |
Not expected to occur during the lifetime of the installation. No record of previous occurrence. |
2 |
||
CASUAL |
The occurrence of the scenario depends on a single fault (human or machine). |
3 |
||
PROBABLE |
Expected an instance of the scenario during the lifetime of the system. |
4 |
||
VERY PROBABLE |
At least one occurrence of the scenario already happened. |
5 |
||
DETECTION |
Description |
Points |
||
VERY |
The system provides for the detection of danger, preventing the occurrence of the incident or accident. |
1 |
||
EASY |
Anyone without any specific training or knowledge of the activity is able to identify the hazard in the activity. |
2 |
||
MODERATE |
The risks will only be identified through analysis by people with specific training and / or knowledge of the activity. |
3 |
||
DIFFICULT |
The danger is identified only reactively (accidents and incidents) or the use of equipment and / or specific monitoring. |
4 |
||
VERY |
There is no way to detect danger or their monitoring and detection is extremely difficult. |
5 |
||
----
MECHANICAL FAILURE MODES |
|||
The following scenarios are presented mechanical risks in the operation of the X device. Check the degree of probability of occurrence, severity if the risk materializes and the detection rate risk. |
|||
QUESTIONS |
ANSWERS |
||
M1) Impact on guidance unit. |
Severity |
Occurrence |
Detection |
M2) Impact of flooding valve. |
Severity |
Occurrence |
Detection |
M3) Impact of the initiator. |
Severity |
Occurrence |
Detection |
M4) Impact of the X device section during movement in crane. |
Severity |
Occurrence |
Detection |
M5) Impact of equipment X device for handling the crane. |
Severity |
Occurrence |
Detection |
M6) Fall of the X device on the transport vehicle. |
Severity |
Occurrence |
Detection |
M7) Fall of the X device on the crane. |
Severity |
Occurrence |
Detection |
----
Expert |
M1 |
M2 |
M3 |
M4 |
||||||||
S |
O |
D |
S |
O |
D |
S |
O |
D |
S |
O |
D |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
2,00 |
3,00 |
2,00 |
4,00 |
2,00 |
2,00 |
5,00 |
2,00 |
3,00 |
4,00 |
1,00 |
3,00 |
2 |
2,00 |
3,00 |
2,00 |
4,00 |
2,00 |
2,00 |
5,00 |
1,00 |
2,00 |
4,00 |
1,00 |
2,00 |
3 |
2,00 |
2,00 |
1,00 |
3,00 |
3,00 |
3,00 |
5,00 |
2,00 |
3,00 |
4,00 |
1,00 |
3,00 |
4 |
4,00 |
4,00 |
1,00 |
5,00 |
3,00 |
4,00 |
5,00 |
3,00 |
4,00 |
5,00 |
1,00 |
4,00 |
5 |
2,00 |
5,00 |
1,00 |
3,00 |
3,00 |
3,00 |
4,00 |
3,00 |
3,00 |
3,00 |
2,00 |
3,00 |
6 |
4,00 |
3,00 |
3,00 |
5,00 |
3,00 |
4,00 |
5,00 |
3,00 |
4,00 |
5,00 |
1,00 |
4,00 |
7 |
2,00 |
4,00 |
3,00 |
5,00 |
2,00 |
4,00 |
5,00 |
2,00 |
4,00 |
5,00 |
1,00 |
4,00 |
8 |
3,00 |
4,00 |
3,00 |
5,00 |
3,00 |
3,00 |
4,00 |
3,00 |
4,00 |
5,00 |
2,00 |
4,00 |
9 |
2,00 |
3,00 |
2,00 |
5,00 |
3,00 |
3,00 |
5,00 |
3,00 |
3,00 |
4,00 |
3,00 |
4,00 |
10 |
2,00 |
3,00 |
3,00 |
3,00 |
2,00 |
3,00 |
4,00 |
3,00 |
3,00 |
4,00 |
2,00 |
4,00 |
11 |
3,00 |
3,00 |
2,00 |
4,00 |
3,00 |
4,00 |
4,00 |
3,00 |
3,00 |
4,00 |
1,00 |
3,00 |
12 |
2,00 |
4,00 |
2,00 |
4,00 |
2,00 |
3,00 |
4,00 |
2,00 |
3,00 |
3,00 |
3,00 |
3,00 |
13 |
1,00 |
5,00 |
2,00 |
3,00 |
3,00 |
2,00 |
3,00 |
3,00 |
2,00 |
5,00 |
1,00 |
2,00 |
14 |
2,00 |
4,00 |
2,00 |
4,00 |
3,00 |
3,00 |
4,00 |
3,00 |
3,00 |
4,00 |
1,00 |
3,00 |
15 |
4,00 |
2,00 |
3,00 |
5,00 |
3,00 |
3,00 |
5,00 |
3,00 |
3,00 |
5,00 |
2,00 |
2,00 |
16 |
2,00 |
4,00 |
2,00 |
4,00 |
2,00 |
2,00 |
4,00 |
2,00 |
2,00 |
4,00 |
2,00 |
2,00 |
17 |
3,00 |
2,00 |
2,00 |
5,00 |
3,00 |
4,00 |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
3,00 |
18 |
2,00 |
3,00 |
2,00 |
5,00 |
3,00 |
4,00 |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
3,00 |
19 |
2,00 |
4,00 |
2,00 |
4,00 |
2,00 |
3,00 |
5,00 |
3,00 |
3,00 |
5,00 |
2,00 |
3,00 |
20 |
3,00 |
3,00 |
3,00 |
4,00 |
3,00 |
4,00 |
4,00 |
3,00 |
4,00 |
5,00 |
1,00 |
4,00 |
21 |
1,00 |
2,00 |
1,00 |
3,00 |
2,00 |
2,00 |
4,00 |
1,00 |
2,00 |
4,00 |
1,00 |
2,00 |
22 |
1,00 |
2,00 |
2,00 |
2,00 |
1,00 |
1,00 |
3,00 |
1,00 |
2,00 |
4,00 |
1,00 |
2,00 |
23 |
3,00 |
3,00 |
2,00 |
4,00 |
2,00 |
3,00 |
5,00 |
3,00 |
3,00 |
5,00 |
3,00 |
3,00 |
24 |
3,00 |
3,00 |
3,00 |
4,00 |
3,00 |
3,00 |
5,00 |
3,00 |
3,00 |
5,00 |
2,00 |
3,00 |
25 |
3,00 |
2,00 |
2,00 |
4,00 |
2,00 |
4,00 |
5,00 |
2,00 |
4,00 |
5,00 |
2,00 |
2,00 |
26 |
2,00 |
2,00 |
3,00 |
4,00 |
3,00 |
3,00 |
4,00 |
3,00 |
3,00 |
5,00 |
3,00 |
3,00 |
27 |
1,00 |
1,00 |
2,00 |
3,00 |
1,00 |
2,00 |
3,00 |
1,00 |
2,00 |
3,00 |
1,00 |
2,00 |
28 |
2,00 |
3,00 |
2,00 |
4,00 |
2,00 |
3,00 |
4,00 |
1,00 |
2,00 |
5,00 |
3,00 |
2,00 |
29 |
2,00 |
2,00 |
2,00 |
3,00 |
1,00 |
2,00 |
4,00 |
1,00 |
3,00 |
4,00 |
3,00 |
2,00 |
30 |
2,00 |
3,00 |
2,00 |
4,00 |
1,00 |
3,00 |
4,00 |
2,00 |
3,00 |
5,00 |
2,00 |
3,00 |
Total |
69,00 |
91,00 |
64,00 |
119,00 |
71,00 |
89,00 |
131,00 |
71,00 |
89,00 |
133,00 |
51,00 |
87,00 |
Mean |
2,300 |
3,033 |
2,133 |
3,967 |
2,367 |
2,967 |
4,367 |
2,367 |
2,967 |
4,433 |
1,700 |
2,900 |
Variance |
0,700 |
0,930 |
0,395 |
0,654 |
0,516 |
0,654 |
0,447 |
0,654 |
0,447 |
0,461 |
0,631 |
0,576 |
mode |
2 |
3 |
2 |
4 |
3 |
3 |
5 |
3 |
3 |
5 |
1 |
3 |
RPN(s) |
|
12,00 |
|
|
36,00 |
|
|
45,00 |
|
|
15,00 |
|
Expert |
M5 |
M6 |
M7 |
||||||
S |
O |
D |
S |
O |
D |
S |
O |
D |
|
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
1 |
5,00 |
2,00 |
2,00 |
4,00 |
1,00 |
3,00 |
3,00 |
3,00 |
3,00 |
2 |
5,00 |
2,00 |
2,00 |
5,00 |
1,00 |
3,00 |
5,00 |
4,00 |
4,00 |
3 |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
2,00 |
5,00 |
5,00 |
4,00 |
4 |
5,00 |
3,00 |
4,00 |
5,00 |
2,00 |
3,00 |
5,00 |
4,00 |
4,00 |
5 |
4,00 |
1,00 |
2,00 |
4,00 |
1,00 |
2,00 |
3,00 |
5,00 |
2,00 |
6 |
5,00 |
2,00 |
3,00 |
5,00 |
1,00 |
3,00 |
4,00 |
4,00 |
4,00 |
7 |
5,00 |
3,00 |
2,00 |
5,00 |
2,00 |
1,00 |
4,00 |
5,00 |
3,00 |
8 |
5,00 |
2,00 |
3,00 |
5,00 |
1,00 |
2,00 |
5,00 |
5,00 |
3,00 |
9 |
5,00 |
2,00 |
3,00 |
5,00 |
1,00 |
1,00 |
5,00 |
5,00 |
3,00 |
10 |
5,00 |
2,00 |
3,00 |
4,00 |
1,00 |
2,00 |
3,00 |
5,00 |
4,00 |
11 |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
1,00 |
4,00 |
5,00 |
4,00 |
12 |
4,00 |
2,00 |
4,00 |
5,00 |
1,00 |
2,00 |
4,00 |
5,00 |
4,00 |
13 |
4,00 |
2,00 |
2,00 |
4,00 |
1,00 |
2,00 |
4,00 |
4,00 |
2,00 |
14 |
5,00 |
3,00 |
2,00 |
4,00 |
1,00 |
2,00 |
4,00 |
5,00 |
4,00 |
15 |
5,00 |
3,00 |
2,00 |
5,00 |
2,00 |
2,00 |
4,00 |
5,00 |
3,00 |
16 |
4,00 |
3,00 |
2,00 |
4,00 |
2,00 |
2,00 |
4,00 |
5,00 |
3,00 |
17 |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
3,00 |
4,00 |
3,00 |
3,00 |
18 |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
2,00 |
5,00 |
5,00 |
3,00 |
19 |
5,00 |
2,00 |
3,00 |
5,00 |
1,00 |
2,00 |
4,00 |
5,00 |
3,00 |
20 |
5,00 |
3,00 |
4,00 |
5,00 |
1,00 |
3,00 |
5,00 |
3,00 |
3,00 |
21 |
4,00 |
1,00 |
4,00 |
3,00 |
1,00 |
2,00 |
4,00 |
5,00 |
2,00 |
22 |
3,00 |
1,00 |
2,00 |
3,00 |
1,00 |
2,00 |
5,00 |
5,00 |
4,00 |
23 |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
1,00 |
5,00 |
5,00 |
3,00 |
24 |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
2,00 |
5,00 |
5,00 |
3,00 |
25 |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
1,00 |
5,00 |
5,00 |
4,00 |
26 |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
1,00 |
5,00 |
5,00 |
3,00 |
27 |
2,00 |
2,00 |
2,00 |
3,00 |
1,00 |
2,00 |
3,00 |
5,00 |
3,00 |
28 |
4,00 |
3,00 |
3,00 |
5,00 |
2,00 |
2,00 |
5,00 |
5,00 |
4,00 |
29 |
4,00 |
3,00 |
2,00 |
5,00 |
1,00 |
2,00 |
5,00 |
3,00 |
3,00 |
30 |
4,00 |
3,00 |
2,00 |
5,00 |
1,00 |
1,00 |
5,00 |
5,00 |
3,00 |
Total |
137,00 |
74,00 |
82,00 |
138,00 |
35,00 |
59,00 |
131,00 |
138,00 |
98,00 |
Mean |
4,567 |
2,467 |
2,733 |
4,600 |
1,167 |
1,967 |
4,367 |
4,600 |
3,267 |
Variance |
0,530 |
0,464 |
0,478 |
0,455 |
0,144 |
0,447 |
0,516 |
0,524 |
0,409 |
mode |
5,00 |
3,00 |
3,00 |
5,00 |
1,00 |
2,00 |
5,00 |
5,00 |
3,00 |
RPN(s) |
|
45,00 |
|
|
10,00 |
|
|
75,00 |
|
----
M1 |
M2 |
M3 |
M4 |
M5 |
M6 |
M7 |
||||||||||||||||
|
S |
O |
D |
S |
O |
D |
S |
O |
D |
S |
O |
D |
S |
O |
D |
S |
O |
D |
S |
O |
D |
|
Inputs |
Mean |
2,3 |
3,0 |
2,1 |
4,0 |
2,4 |
3,0 |
4,4 |
2,4 |
3,0 |
4,4 |
1,7 |
2,9 |
4,6 |
2,5 |
2,7 |
4,6 |
1,2 |
2,0 |
4,4 |
4,6 |
3,3 |
Standard Deviation |
0,8 |
1,0 |
0,6 |
0,8 |
0,7 |
0,8 |
0,7 |
0,8 |
0,7 |
0,7 |
0,8 |
0,8 |
0,7 |
0,7 |
0,7 |
0,7 |
0,4 |
0,7 |
0,7 |
0,7 |
0,6 |
|
Outpus |
RPN(s) |
15 |
28 |
31 |
22 |
31 |
11 |
66 |
||||||||||||||
1. Professor Doutor, no Mestrado na Universidade Santa Úrsula, Rio de Janeiro, Brasil. eduardoferrazuff@yahoo.com.br ;
2. Professor Doutor, no Curso de Engenharia de Produção na Universidade Federal Fluminense, Rio de Janeiro, Brasil. glima@id.uff.br
3. Professor Doutor, no Curso de Engenharia de Produção na Universidade Federal Fluminense, Rio de Janeiro, Brasil. annibal.parracho@gmail.com
4. Engenheiro , Comissão Nacional de Energia Nuclear, Rio de Janeiro, Brasil. rfonseca@cnen.gov.br
5. Engenheiro , Comissão Nacional de Energia Nuclear, Rio de Janeiro, Brasil. pmaffia81@gmail.com
6. Doutorando, Engenharia de Produção na Universidade Federal Fluminense, Rio de Janeiro, Brasil. luiz.gaviao67@gmail.com