Espacios. Vol. 36 (Nº 09) Año 2015. Pág. 10

Otimização de padrões de cortes bidimensionais guilhotinados restritos

Optimization of two-dimensional slit cuts restricted patterns

Fábio Moacir HOFFMANN 1; André Luiz Emmel SILVA 2; Elpídio Oscar Benitez NARA 3; Rafael Alvise ALBERTI 4; Jacques Nelson Corleta SCHREIBER 5

Recibido: 13/01/2015 • Aprobado: 13/02/2015

Contenido

1. Introdução

2. Materiais e métodos

3. Revisão bibliográfica

4. Resultados e discussão

5. Considerações finais

6. Referências

1. Introdução

A competitividade, alta em diversos setores da indústria, impõe às empresas uma busca constante por melhorias em seus produtos e processos produtivos. Alternativas que viabilizem maximizar o uso dos insumos sem efeitos indesejáveis, além de manter a qualidade do produto final são bem vindas nas indústrias, representando economia financeira e vantagens competitivas.

Em organizações que oferecem produtos sob medida, os sistemas apresentam grandes capacidades ociosas e dificuldade de padronização dos métodos de trabalho, o que acaba inibindo a possibilidade de automação, encarecendo o produto (LUSTOSA et al., 2008). Quando empresas desse ramo se especializam e aprimoram seus processos de planejamento de projeto e desenvolvimento, conseguem atender às demandas de produtos customizados em menor espaço de tempo.

O corte de matéria-prima é uma etapa básica e importante no processo produtivo de diversas empresas (KATSURAYAMA e YANASSE, 2004). Belluzzo e Morabito (2005) relatam a importância da programação de corte para o planejamento e controle da produção devido à influência dessa etapa nos custos com desperdícios e na produtividade da empresa. Por isso, a formulação de padrões de corte pode ser de grande valia uma vez que mostram como as chapas devem ser cortadas e consistem em otimizar custos da produção, desperdícios, entre outros (PINTO e YANASSE, 2001).

O processo de corte ocasiona uma perda de matéria-prima e, por conseguinte, aumento de custos, podendo até mesmo, comprometer a competitividade da indústria (TEMPONI, 2007). Com isso, surge um problema de aproveitamento e a busca pela otimização que compreende cortar as peças nas quantidades necessárias para fabricação com a menor perda possível.

De acordo com a programação das máquinas e a escala de produção, as perdas podem chegar a toneladas, representando custos consideráveis. Parte desse desperdício pode ser evitada apenas com melhorias no planejamento de corte sem necessitar de investimentos adicionais em capacidade.

Um dos pontos importantes na otimização do aproveitamento de matéria-prima se dá na possibilidade de oferecer produtos e serviços que agregam valor aos consumidores e contribuem para sua satisfação. Por isso, as empresas devem adequar seus processos para eliminar os desperdícios, manter as atividades que agregam valor e eliminar de forma sistêmica aquelas que não agregam (FILHO, 2002).

Nesse contexto, a otimização de padrões de corte torna-se uma importante ferramenta de melhoria em eficiência e sendo assim, o artigo tem por objetivo propor a utilização de uma ferramenta de otimização de padrões de corte bidimensionais restritos. Além disto, analisar os resultados desta utilização, sem modificar a qualidade e as funcionalidades dos produtos.

2. Materiais e métodos

A empresa em estudo situa-se no estado do Rio Grande do Sul - Brasil, oferecendo produtos nos segmentos de informação e entretenimento. Os produtos com foco em informação buscam atender necessidades mais sofisticadas e complexas, especialmente em eletrônica e software. Enquanto que no ramo do entretenimento, os produtos são voltados ao lazer familiar e infantil.

O trabalho limita-se a abordar os aspectos que envolvem o processo de corte de painéis de MDF (Medium Density Fiberboard), que integram as matérias-primas da marcenaria. O processo analisado utiliza serras circulares e a operação dos batentes e avanço da mesa ocorrem de forma manual. Foi considerada a segmentação de chapas com formas geométricas retangulares (bidimensionais), ou seja, figuras em que todos os lados formam ângulos retos entre si e cada corte origina dois novos retângulos (corte guilhotinado). Levando-se em conta que as chapas têm tamanhos finitos, existe também um limite de peças que podem ser obtidas a partir de uma chapa (problema restrito). Portanto, trata-se de um problema de cortes bidimensionais guilhotinados restritos.

Sob a ótica dos procedimentos técnicos, o estudo em questão pode ser classificado como pesquisa-ação. Os procedimentos metodológicos dividiram-se em 4 etapas. Na primeira etapa buscou-se um referencial teórico em livros, artigos, dissertações de mestrado e teses de doutorado. Na segunda etapa procurou-se identificar as particularidades da operação de corte na empresa, possíveis limitações de processo e as quantidades de itens, sobras e retalhos gerados durante as observações. Para tanto, utilizou-se de observação, entrevistas não estruturadas e quantificação através do somatório das áreas dos elementos em questão. Além disso, realizou-se um levantamento da quantidade e custos dos painéis de MDF consumidos nos últimos anos com dados obtidos a partir do sistema de gestão da empresa. Na etapa 3, formulou-se uma nova proposta de trabalho considerando as limitações do processo e dados obtidos. Simulações foram realizadas através do software Maxcut, um recurso gratuito, que permite a otimização de cortes bidimensionais guilhotinados restritos. Na última etapa os dados obtidos através da observação do processo foram comparados com dados simulados para avaliar se a proposta pode ser considerada eficaz em atender aos objetivos.

3. Revisão bibliográfica

3.1 Problema de corte

As primeiras discussões na literatura em torno dos problemas de corte foram introduzidas por Gilmore e Gomory, em 1961, com problemas unidimensionais. Com o passar do tempo, foram propostos diversos métodos para resolução de problemas unidimensionais, bidimensionais e até tridimensionais (TEMPONI e SANTOS, 2007). Os problemas de corte consistem basicamente em definir a forma de cortar chapas (objetos) para produzir as peças (itens), nas respectivas quantidades, com o menor desperdício possível de material (PINTO e YANASSE, 2001; BELLUZZO e MORABITO, 2005; TEMPONI e SANTOS, 2007; VELASCO, 2008).

Problemas de corte são de fácil representação matemática, porém, de difícil resolução devido à sua complexidade uma vez que se deseja minimizar uma função que contém diversas variáveis sujeitas a um conjunto de restrições. Ainda que haja um número finito de soluções, a simples enumeração destas pode tomar grandes dimensões. Além disso, ao nível de resolução, problemas que envolvem rotação de itens são mais complexos já que são consideradas todas as rotações possíveis (TEMPONI, 2007).

3.1.1 Padrões de corte

Na busca pela otimização de cortes, costuma-se utilizar o chamado padrão de corte, definido como a disposição de peças na área disponível em uma placa. Para isso, deve-se respeitar dois princípios básicos: todo e qualquer item deve caber inteiramente no objeto atribuído; e não deve haver sobreposição de itens quando da colocação no objeto. Além disso, as limitações devido ao tipo de indústria e aos equipamentos de corte devem ser respeitadas (TEMPONI e SANTOS, 2007). Para tanto, Gramani (2001) afirma que é preciso adotar algumas regras para formular um padrão de corte, como a natureza dimensional da segmentação (unidimensional, bidimensional ou tridimensional), a exigência por cortes guilhotinados, a limitação da quantidade de peças (problema restrito) e o número de estágios.

Figueiredo e Rangel (2006), por sua vez, consideram importantes para viabilidade e qualidade do padrão de corte, além da composição de cortes guilhotinados e do número de estágios, o cuidado com o número de faixas de larguras distintas e a quantidade de peças que a seccionadora consegue cortar de uma só vez.

3.1.2 Características dimensionais do corte

Os problemas de corte são classificados de acordo com as dimensões importantes para o processo e, em resumo, podem ser unidimensionais, bidimensionais ou tridimensionais. Os cortes unidimensionais ocorrem quando somente uma dimensão (comprimento) é relevante para o corte, por exemplo, para o seccionamento de barras de aço ou cabeamento de cobre.

Cortes bidimensionais, são executados usualmente em chapas de madeira e placas de fibra de vidro para confecção de placas de circuito impresso. O problema de corte caracteriza-se como bidimensional quando duas dimensões (largura e comprimento) dos itens e objetos são fundamentais para a sua solução (GRAMANI, 2001; MORABITO e PUREZA, 2007; TEMPONI, 2007; GHIDINI, 2008; VELASCO, 2008). Os padrões de corte bidimensionais apresentam formulação consideravelmente mais difícil se comparado aos casos unidimensionais, pois, além das limitações físicas uma série de regras de como os itens serão dispostos sobre o objeto pode ser necessária (PINTO, 2004). A figura 1 mostra exemplos de corte unidimensional ( a ), bidimensional ( b ) e tridimensional ( c ).

Figura 1 – Corte unidimensional (a), bidimensional (b) e tridimensional (c)

Fonte: Adaptado de Pinto (2004) e Ghidini (2008)

Alguns autores ainda ramificam a classificação de acordo com características especiais dos objetos a serem cortados. Ghidini (2008) e Pinto (2004) ainda citam os problemas 1,5 unidimensional, que trata de problemas bidimensionais onde a largura é fixa, mas o comprimento é suficientemente grande, por exemplo, no caso de uma bobina de aço e problemas 2,5 dimensional, por exemplo, com largura e altura fixos e comprimento suficientemente grande.

3.1.3 Cortes guilhotinados

Devido às limitações de maquinário, um dos fatores que devem ser levados em conta é a busca por padrões que possibilitem cortes guilhotinados. Um corte é chamado de guilhotinado quando aplicado a uma chapa retangular produz dois novos retângulos (FIGUEIREDO e RANGEL, 2006; TEMPONI, 2007; CHERRI e VIANNA, 2012). Com outros termos, Ghidini (2008) afirma que cortes guilhotinados são aqueles realizados paralelamente a um dos lados e que percorre toda a extensão do objeto.

Observa-se na figura 2 que o corte guilhotinado (a) pode ser executado do início ao fim da chapa de forma ininterrupta. No entanto, os cortes não guilhotinados (b, c) não podem ser executados sem que sejam interrompidos para rotação do objeto ou da serra.

Figura 2 – Corte guilhotinado (a) e cortes não guilhotinados (b) (c)

Fonte: Adaptado de Pinto (2004) e Ghidini (2008)

3.1.4 Problema restrito

O problema de corte do tipo restrito é aquele em que as chapas (matéria-prima) têm tamanhos limitados e padronizados. Os padrões de corte são restritos quando existe limitação do número de vezes que uma peça pode ser obtida a partir de uma chapa (MORABITO e PUREZA, 2007; TEMPONI, 2007). Essa característica ocorre também devido às dimensões limitadas do objeto e em situações de baixa demanda de itens (GHIDINI, 2008).

3.1.5 Estágios de corte

O corte inicial representa o 1° estágio e, a partir daí, cada vez que a peça é rotacionada a 90° para executar o corte seguinte, tem-se um estágio e, consequentemente, um consumo de tempo e energia do operador (KATSURAYAMA e YANASSE, 2004; FIGUEIREDO e RANGEL, 2006).

O corte também pode ser exato ou não exato. Um padrão 2-estágios exato é aquele que resulta em todos os itens cortados ao final do segundo estágio. Se mais cortes forem necessários, o padrão é chamado 2-estágios não exato (PINTO, 2004; FIGUEIREDO e RANGEL, 2006; GHIDINI, 2008). A figura 3 mostra um padrão 2-estágios exato.

Figura 3 – Padrão de corte bidimensional guilhotinado 2-estágios exato

Fonte: Adaptado de Katsurayama e Yanasse (2004) e Pinto (2004)

Katsurayama e Yanasse (2004) afirmam, que padrões de corte com mais estágios reduzem ainda mais o desperdício de material, mas exigem maior número de rotações, representando um aumento no tempo de corte. Por isso, em algumas situações considera-se padrões de corte com menos estágios visando menos tempo de processamento.

Padrões simples de execução podem ser obtidos através da criação de padrões tabuleiros. Nesse tipo de padrão, após o primeiro estágio de corte, as faixas estão prontas para serem cortadas simultaneamente no segundo estágio, resultando na produção dos itens necessários. Estes padrões tabuleiros imprimem baixo custo produtivo, pois requerem pouco manuseio. Pinto (2004) concorda que esses padrões aceleram o processo, mas lembra que em contrapartida podem haver maiores índices de perda de material. Pela figura 4 é possível perceber que, no segundo estágio, todas as faixas originadas no primeiro podem ser cortadas simultaneamente.

Figura 4 – Padrão de corte bidimensional guilhotinado 2-estágios tabuleiro

  Fonte: Adaptado de Katsurayama e Yanasse (2004) e Figueiredo e Rangel (2006)

Ainda que a máquina não ofereça essa possibilidade, o padrão tabuleiro é vantajoso, pois as faixas do segundo estágio podem ser cortadas com menos regulagens no batente que determina a largura da faixa a ser seccionada. Para o corte com serra de batente manual, outro cuidado que se deve ter na construção de um padrão de corte se refere à quantidade de faixas com larguras diferentes. A cada faixa de largura diferente, existe um processo de regulagem do batente que determina uma das dimensões a serem cortadas (FIGUEIREDO e RANGEL, 2006).

3.2 MDF (Medium Density Fiberboard)

Definido pela Associação Brasileira da Indústria de Painéis de Madeira – ABIPA (2013) como um painel industrial homogêneo, com excelente estabilidade dimensional, de superfície uniforme, lisa e de alta densidade. Portanto, o MDF é um material não disponível diretamente na natureza.

Basicamente são usados dois tipos de MDF: o MDF in natura ou cru; e o MDF melamínico. O MDF in natura é aquele que não recebe acabamento pelo fabricante, ficando a cargo do processador, que escolhe a forma que irá fazê-lo. O MDF melamínico, por sua vez, tecnicamente chamado de laminado de baixa pressão (BP), é aquele que recebe uma "lâmina celulósica impregnada com resina melamínica que, com alta temperatura e pressão, é fundida aos painéis de madeira, resultando em um painel pronto para uso". A lâmina do MDF laminado apresenta grande resistência a riscos, facilita a limpeza e diminui a proliferação de micro organismos. Ademais, tem a vantagem de estar pronta para o uso e, dependendo da aplicação, não necessita de nenhum acabamento adicional (ABIPA, 2013).

3.3 Desperdícios por processos inadequados

Encarado cada vez mais como algo a ser evitado, o desperdício ainda faz parte do cotidiano das indústrias e sociedade por diversos motivos. Na produção, há muito já existe essa preocupação. De acordo com Ohno (1997), considerado um dos responsáveis pelo Sistema Toyota de Produção, desperdício é aquilo que gera custos sem agregar valor. Desta forma, para alcançar o lucro, o produto deve gerar mais valor do que os custos e, como os desperdícios se transformam em custos, são contrários ao lucro (FILHO, 2002).

Dentre os sete principais tipos de desperdícios, constatados no Sistema Toyota de Produção está o desperdício por processos inadequados. Se referindo ao uso de ferramentas, procedimentos ou sistemas inadequados de processo que, em muitos casos, poderiam ser realizados de forma mais simples (HINES e TAYLOR, 2000). Esses desperdícios constituem uma parte do processo que poderia ser eliminada, uma vez que configuram atividades desnecessárias para alcançar as características e funções desejadas pelos clientes.

No que diz respeito aos processos de corte, um baixo aproveitamento das chapas de MDF certamente não agrega valor ao produto, pois gera custos considerados, muitas vezes, inaceitáveis aos consumidores. Os resíduos representam a perda de um recurso já pago pela indústria, ao qual se devem somar os gastos com manuseio e disposição final (HOLZSCHUH, 2008). Desta forma uma economia no volume de materiais representa uma redução no impacto ambiental por que menos materiais são produzidos e, por conseguinte, diminui-se o uso de transporte e necessidade de descarte.

Figueiredo e Rangel (2006) em estudo realizado em uma indústria de móveis de médio porte do pólo de Votuporanga, no noroeste do estado de São Paulo, apontaram um índice de aceitação de perdas abaixo de 6% da área do objeto. Hillig et al. (2009), por sua vez, realizaram um estudo da geração de resíduos em 94 empresas do polo moveleiro da Serra Gaúcha, encontrando índices de aproveitamento de matérias-primas de 94,51% para MDF e 94,9% para o aglomerado.

3.4 Software Maxcut

O software MaxCut, concebido pela Maxima Software Ltda, tem a função de otimizar padrões de cortes bidimensionais (MAXCUT, 2013). É um recurso gratuito e, por isso, permite que seja testado livremente. O funcionamento do software segue as seguintes etapas:

• Entradas: informa-se o material e as dimensões dos painéis (objetos) e das peças (itens). Nas dimensões dos itens, pode-se ainda incluir uma compensação devido às fitas de borda, comumente utilizadas como forma de acabamento das faces cortadas. Na etapa das entradas, é possível importar e exportar a lista de materiais (itens, dimensões, quantidades, necessidade de fitas de borda) de planilhas eletrônicas, guardando os dados de cada produto tornando o processo mais ágil e diminui a possibilidade de erros de digitação.
• Parametrização: informa-se a espessura da lâmina de corte e escolhe-se a qualidade da otimização, o número de estágios de corte desejados, a forma de encaixe dos itens e se é permitida a rotação destes. Uma qualidade de otimização melhor, consome mais tempo de cálculo. Para o encaixe dos itens, existem duas opções: Cortes do primeiro estágio seguem no sentido longitudinal (comprimento) ou no sentido transversal (largura).
• Saídas: é um padrão de corte que mostra como os itens devem ser dispostos sobre os objetos, quantos painéis são necessários para execução do trabalho completo, o comprimento de corte, o desperdício do objeto e do trabalho todo. A figura 5 mostra a tela de saídas do software. É necessário ressaltar que o software não faz distinção entre sobras e retalhos, podendo acarretar em um índice de perda mais alto que o real.

  Figura 5 – Saídas do software

Fonte: Software MaxCut (2013)

4. Resultados e discussão

4.1 Caracterizações do ambiente

Observando o volume de materiais desperdiçados pelo setor de marcenaria da empresa em estudo, notou-se a oportunidade de buscar e analisar possibilidades para minimizar os desperdícios das matérias-primas mais utilizadas. Somado a isso, não há na empresa nenhuma ferramenta para auxiliar no planejamento de corte de chapas. Sendo assim, a sequência e disposição dos cortes sobre a chapa não são planejadas e contam apenas com o conhecimento individual dos trabalhadores, não tendo nenhum procedimento padrão. Esta falta de rotina é justamente o fator que dificulta essa padronização. Conforme acontecem as vendas, os produtos devem ser produzidos e possivelmente, todo dia serão cortadas peças diferentes.

Diversos produtos e também algumas embalagens possuem uma ou mais peças em MDF, tornando o processo de corte uma etapa importante, já que precede os demais processos de manufatura desses produtos. Para a execução desse processo podem ser usados painéis virgens ou, conforme disponibilidade e conhecimento dos funcionários, sobras de cortes anteriores.

Normalmente, os processos seguintes ao corte são a usinagem ou a montagem. A principal diferença é que cortes para montagem devem ser efetuados nas medidas exatas enquanto cortes para usinagem devem ser ligeiramente maiores. Após o término do corte de um painel, obtêm-se diferentes grupos de materiais que podem ser classificados em itens, sobras, retalhos, além do pó e serragem, conforme exemplo mostrado na figura 6.

Figura 6 – Distribuição dos materiais conforme utilidade

Fonte: Elaborado pelos autores

• Itens são os produtos resultantes ao final de cada parte do processo. Ao final do processo de corte, apresentam a forma retangular e estão prontas para seguirem para a próxima etapa do processo produtivo. As sobras não fazem parte dos itens necessários, mas considera-se que ainda podem ser usadas para fabricação de novos itens. Atualmente, o que é considerado sobra ou resíduo não segue uma regra formal, e sim depende da experiência e bom senso dos funcionários da área. As peças desse tipo são estocadas em uma prateleira até que o funcionário a insira novamente em alguma parte do processo, até mesmo no corte. Por isso, é preferível que existam menos sobras e com dimensões maiores, fazendo com que sejam mais facilmente aproveitadas, uma vez que quanto maior o objeto, mais itens podem ser obtidos a partir deste. Retalhos são peças remanescentes, demasiadamente pequenas, que não são mais consideradas úteis na fabricação de novos itens, ou seja, não são itens e nem sobras.

Para entender a evolução do consumo do MDF realizou-se um levantamento referente ao período de 2009 a 2013, mostrado a figura 7. 

Figura 7 – Consumo de MDF entre 2009 e 2013

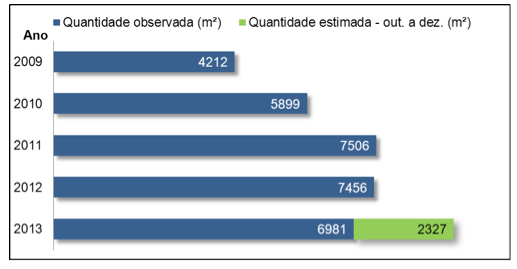
Fonte: sistema de gestão da empresa

Para efetuar o acompanhamento do processo, estabeleceu-se que a entrada de matéria-prima seria apenas na forma de painéis inteiros. Essa determinação deve-se à variação do volume e dimensões das sobras, ou seja, determinada combinação de períodos e produtos pode ser favorável ou não à utilização de sobras, obtendo-se, portanto, mais ou menos itens.

4.2 Proposta de ferramenta de otimização de padrões de corte

Como proposta para otimização dos padrões de corte, propõe-se o uso do software MaxCut, no qual foram gerados padrões de corte a fim de obter dados para a comparação com os dados observados. A geração dos padrões de corte seguiu as 3 etapas necessárias.    Na etapa de informar as entradas, certificou-se que as quantidades, materiais e dimensões dos itens eram idênticos àqueles cortados no setor de marcenaria. Na etapa de parametrização do software, a qualidade de otimização foi definida como a melhor possível devido ao baixo tempo de cálculo dos padrões simulados (menos de 5 segundos) e permitiu-se a rotação dos itens. Como espessura da serra, aplicou-se 3 mm, da mesma forma que ocorre na realidade. Quanto à forma de encaixe dos itens, foram gerados, num primeiro momento, seis opções de padrão de corte:

1. 2-estágios com primeiro estágio na longitudinal;
2. 2-estágios com primeiro estágio na transversal;
3. 3-estágios com primeiro estágio na longitudinal;
4. 3-estágios com primeiro estágio na transversal;
5. 4-estágios com primeiro estágio na longitudinal;
6. 4-estágios com primeiro estágio na transversal.

Esses padrões foram discutidos com os operadores, sendo os padrões de 4-estágios refutados em virtude da dificuldade de realização dos cortes e possível aumento no consumo de tempo, tornando-os inviáveis. As opções 2-estágios e 3-estágios foram consideradas viáveis, mas existe uma preferência por padrões com o primeiro estágio na longitudinal. Após diversos testes realizados pelo autor antes dos padrões definitivos, percebeu-se que, para os casos analisados, os cortes 2-estágios apresentaram os mesmo índices de aproveitamento dos padrões 3-estágios, todavia, com execução mais simples. Portanto, para todos os testes realizados, trabalhou-se somente com padrões 2-estágios com o primeiro corte no sentido longitudinal com a finalidade principal de facilitar os cortes a serem realizados.

4.3 Resultados encontrados

Para fins de padronização, definiu-se como sobras as peças que possuem largura e área mínimas de 150 mm e 90.000 mm², respectivamente. Essas definições foram feitas a partir de medições realizadas nas caixas de retalhos e entrevistas não estruturadas com os colaboradores da área. Os dados referentes a produção de 54 produtos estão mostrados na tabela 1, sendo que cada um dos cinco indicadores monitorados foi dividido em "observado" e "proposto".

Tabela 1 – Resultados encontrados

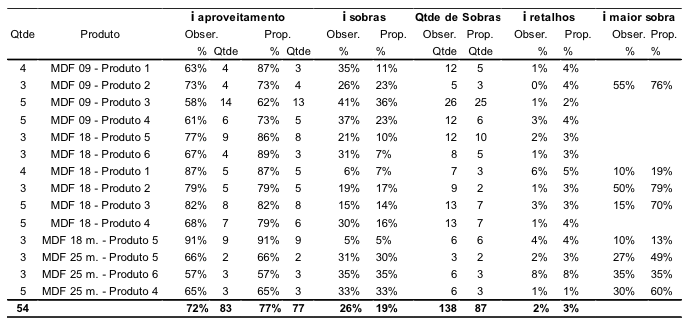
Fonte: Elaborado pelos autores

4.3.1 Índice de aproveitamento de painéis virgens

O índice de aproveitamento de painéis virgens refere-se ao percentual de conversão desses painéis em itens. Um índice de 70%, por exemplo, representa que 70% da área total dos painéis transformaram-se em itens, sendo o restante dividido entre sobras, retalhos e desgaste por serra. Dessa forma, um índice maior representa a necessidade de menos painéis para obter os mesmo itens. Os resultados foram obtidos através da equação 1:

Observa-se que houve uma redução do número de painéis necessários em 43% dos casos mostrados. Somando-se todos os casos, houve uma redução de 83 para 77 painéis necessários, representando aproximadamente 7% da quantidade total.

4.3.2 Índice de sobras

Esse índice refere-se ao percentual dos painéis utilizados que se tornou sobra, ou seja, que será estocado novamente até que possa ser utilizado posteriormente. Vale lembrar que as sobras, apesar de ainda terem condições de uso, apresentam diversas desvantagens como relatado anteriormente no tópico de explanação de sobras. Portanto, índices de sobras menores são considerados mais satisfatórios. Esse indicador foi encontrado a partir da equação 2:

Referente ao modelo proposto, 70% dos casos observados apresentaram redução no índice de sobras sendo que parte desses resultados foram influenciados diretamente da melhoria no índice de aproveitamento de painéis virgens. Os demais devem-se por uma mudança na distribuição entre sobras e retalhos.

4.3.3 Quantidade de sobras

Esse indicador mostra o número de peças unitárias consideradas sobras, sendo sua importância dada pelo fato de reduções dessas quantidades representarem área unitária maior. Por exemplo, se o índice de sobras foi de 50%, dividido em 5 peças, tem-se uma área média de 10% por sobra. Se, com esse mesmo índice de sobras, a quantidade de unidades for reduzida para 2, tem-se uma área média de 25% por sobra.

Verificou-se que o modelo proposto apresentou apenas 63% do número de sobras geradas nos casos observados, significando, portanto, uma considerável redução.

4.3.4 Índice de retalhos

Esse índice também é consequência dos índices de aproveitamento e da distribuição entre sobras e retalhos, mas é válido listar esse resultado para fins de conhecimento. Esses valores foram encontrados a partir da equação 3:

Constatou-se que o modelo proposto apresentou um aumento no percentual de retalhos em 9 dos 14 casos. Em 4 casos, não houve diferenças e em apenas 1 houve uma redução. Embora signifiquem o percentual que será descartado imediatamente, não é possível afirmar que índices ligeiramente maiores representam padrões de corte menos eficientes. Um padrão de corte pode comumente apresentar um aproveitamento melhor dos painéis e ainda assim resultar em um maior índice de retalhos. Nesses casos, espaços vazios antes classificados como sobras são ocupados por itens e retalhos.

4.3.5 Área da maior sobra

No índice de aproveitamento, diversos casos apresentaram igualdade entre o real e o simulado, pois não houve diferença na quantidade de painéis utilizados. Ainda assim, é possível que existam diferenças na otimização desses padrões. A fim de aprofundar a análise, propôs-se verificar a área da maior sobra nos casos em que não houve diferença no índice de aproveitamento. Na maioria das ocasiões, a maior sobra constitui-se a partir do último painel cortado e aumentos nas áreas dessas peças significam que mais itens foram obtidos a partir dos painéis anteriores. Os valores da maior sobra foram obtidos a partir da equação 4.

4.4 Discussão dos resultados

Para auxiliar na compreensão da importância de cada um dos resultados, formulou-se um exemplo da comparação dos índices de dois padrões de corte.

Nesse exemplo, existe a seguinte necessidade de produção:

• 04 unidades do item A (cada uma consome 20% da área de um painel);
• 02 unidades do item B (cada uma consome 6% da área de um painel);
• 01 unidade do item C (cada uma consome 28% da área de um painel).

Para produção dos itens do exemplo, a figura 8 mostra dois exemplos de padrões de corte fictícios, sendo o padrão ( a ) semelhante aos padrões observados na realidade e o padrão ( b ) semelhante aos padrões propostos pela ferramenta Maxcut.

Figura 8 – Distribuição das sobras com exemplo de caso semelhante ao observado (a) e caso semelhante ao gerado pela ferramenta (b)

Fonte: Elaborado pelos autores

A partir dos dados da figura 8, obteve-se os resultados comparativos da tabela 2. Nota-se que os padrões de corte dos exemplos ( a ) e ( b ) apresentaram os mesmos índices de aproveitamento uma vez que utilizaram a mesma quantidade de painéis virgens, mas no exemplo ( b ) foi possível alocar uma unidade a mais do item A no 1º painel. A diferença mais significativa fica por conta da distribuição de sobras e retalhos. Enquanto que o exemplo ( a ) não apresentou a geração de retalhos, no exemplo ( b ) esse percentual foi de 3%. Porém, no exemplo ( b ) houve uma considerável redução do número de sobras, sendo que a maior delas representa quase 60% de um painel virgem. Com essa sobra, poderiam ser obtidos mais unidades de qualquer dos itens A, B ou C, enquanto que no exemplo ( a ) poderiam ser obtidos apenas unidades dos itens A ou B das sobras.

Tabela 2 – Exemplo de comparativo de indicadores de padrões de corte

Fonte: Elaborado pelos autores

5. Considerações finais

Para a busca de melhorias, é essencial conhecer o processo produtivo, sua finalidade, limitações e funcionamento. Nessas etapas, foi possível compreender o que é importante para que a implementação de uma nova ferramenta seja aceita. Ainda durante a observação do processo produtivo, foi possível levantar os dados necessários que resultaram nos índices de aproveitamento e representatividade das sobras e desperdícios. Esses dados foram a base para chegar-se aos resultados reais, ou seja, quais os números atuais do processo.

Como proposta ao modelo atual de trabalho, aplicou-se o software de otimização de cortes bidimensionais guilhotinados restritos MaxCut. Com ele, conseguiu-se simular padrões de corte e obter os resultados. Analisando tais resultados por comparações, foi possível afirmar que a proposta apresenta uma redução do número de painéis necessários em 43% dos casos observados. Além disso, ocorreu uma redução de 7% do número total de painéis virgens necessários para o corte dos lotes observados. Houve uma redução de percentual de sobras em 70% dos lotes observados. A quantidade de sobras em sofreu redução em 93% dos casos observados. Dentre os lotes que não tiveram redução no número de painéis virgens, 83% apresentaram aumento da área útil na maior sobra.

Conclui-se, portanto, que essa ferramenta mostrou-se uma opção interessante no que se refere à otimização dos padrões de corte bidimensionais guilhotinados restritos. Balizando um aumento no aproveitamento da matéria-prima e consequente redução na quantidade de painéis necessários. Houve também uma diminuição na geração de sobras, facilitando a utilização futura e estocagem desse material.

O uso de simulações de corte pode ser uma ferramenta importante para o setor de planejamento e compras da empresa no que se refere à previsão de consumo e aquisição de quantidades mais próximas às necessárias. Medidas que visam a otimização do uso dos recursos representam, além de benefícios financeiros, uma vantagem competitiva e na forma que a empresa é vista pela sociedade e pelos próprios funcionários.

6. Referências

ABIPA - Associação Brasileira da Indústria de Painéis de Madeira. Nossos Produtos. MDF - Medium Density FiberBoard - Painéis de Fibra de Média Densidade. Disponível em: <http://www.abipa.org.br/ produtosMDF.php>. Acesso em: 05 maio 2013.

BELLUZZO, Luciano; MORABITO, Reinaldo. 2005. Otimização nos padrões de corte de chapas de fibra de madeira reconstituída: Um estudo de caso. Pesquisa Operacional, v. 25, n. 3, p. 391-415.

CHERRI, Adriana; VIANNA, Andréia. 2012. Problemas de corte com itens retangulares e do tipo L. In: XXXIV Congresso de Matemática Aplicada e Computacional, 2012, Natal. Anais... Natal: CMAC.

FIGUEIREDO, Altamir G. de; RANGEL, Socorro. 2006. Geração de padrões de corte produtivos para a indústria de móveis. In: XXXVIII Simpósio Brasileiro de Pesquisa Operacional, 2006, Goiânia. Anais... Goiânia: SBPO.

FILHO, D. J. M. et al. 2002. Custo do desperdício nas empresas industriais. In: XXII Encontro Nacional de Engenharia de Produção, 2002, Curitiba. Anais... Curitiba: ENEGEP.

GHIDINI, Carla Taviane Lucke da Silva. 2008. Otimização de processos acoplados: programação da produção e corte de estoque. 151 f. Tese (Instituto de Ciências Matemáticas e de Computação – Doutorado) – Universidade de São Paulo, São Paulo.

GRAMANI, Maria Cristina Nogueira. 2001. Otimização do processo de cortagem acoplado ao planejamento da produção. 121 f. Tese (Faculdade de Engenharia Elétrica e de Computação – Doutorado) - Universidade Estadual de Campinas, Campinas.

HINES, Peter; TAYLOR, David. 2000. Going Lean. A guide to implementation. Cardiff, UK: Lean Enterprise Research Centre Cardiff Business School.

HILLIG, É; SCHNEIDER, V. E.; PAVONI, E. T. 2009. Geração de resíduos de madeira e derivados da indústria moveleira em função das variáveis de produção. Produção, v. 19, n. 2, p. 292-303.

HOLZSCHUH, G. G. et al. 2008. Otimização dos processos na indústria de ráfia: com enfoque no mapeamento dos processos e na geração de resíduos. In: XXVIII Encontro Nacional de Engenharia de Produção, 2008, Rio de Janeiro. Anais... Rio de Janeiro: ENEGEP.

LUSTOSA, L. et al. 2008. Planejamento e Controle da Produção. Rio de Janeiro: Elsevier.

KATSURAYAMA, Daniel Massaru; YANASSE, Horacio Hideki. 2004. Um algoritmo para geração de padrões tabuleiros exatos a partir de uma combinação dada de itens. In: XXXVI Simpósio Brasileiro de Pesquisa Operacional , 2004, São João del-Rei. Anais... São João del-Rei: SBPO.

MAXCUT. Desenvolvido por Maxima Software Ltda. 2013. Apresenta informações gerais sobre o software. Disponível em: <http://www.maxcut.co.za/>. Acesso em: 05 ago 2013.

MORABITO, Reinaldo.; PUREZA, Vitória. 2007. Geração de padrões de cortes bidimensionais guilhotinados restritos via programação dinâmica e busca em grafo-e/ou. Revista Produção. São Paulo, v.17, n.1, p. 33-51.

OHNO, Taiichi. 1997. O sistema Toyota de produção: além da produção em larga escala. Porto Alegre: Artes Médicas.

PINTO, Maria José. 2004. Algumas contribuições à resolução do problema de corte integrado ao problema de sequenciamento dos padrões. 2004. 196 f. Tese (Curso de Pós-Graduação em Computação Aplicada - Doutorado). Instituto Nacional de Pesquisas Espaciais, São José dos Campos.

PINTO, Maria José; YANASSE, Horacio Hideki. 2001. O Problema de Corte e Sequenciamento de Padrões: uma Abordagem Integrada. In: I WORCAP - Workshop dos Cursos de Computação Aplicada do Inpe, 2001, São José dos Campos. Anais... São José dos Campos: INPE, 2001. p 109-111.

TEMPONI, E. C. C. 007. Uma proposta de resolução do problema de corte bidimensional via abordagem metaheurística. Dissertação (Mestrado em Modelagem Matemática Computacional) - Centro Federal de Educação Tecnológica de Minas Gerais, Belo Horizonte.

TEMPONI, E. C. C.; SANTOS, F. A. 2007. Uma metaheurística híbrida grasp-ils aplicada à solução do problema de corte bi-dimensional guilhotinado. In: XXXIX Simpósio Brasileiro de Pesquisa Operacional, Fortaleza. Anais... Fortaleza.

VELASCO, A. S.; PAULA JUNIOR, G.G.; VIEIRA NETO, E. 2008. Um Algoritmo Heurístico Baseado na GRASP para o Problema de Corte Bidimensional Guilhotinado e Restrito. Revista GEPROS, ed.1, p.129–141.

1. Email: compras@rebelli.com.br
2. Email: andresilva@unisc.br
3. Email: elpidio@unisc.br
4. Email: alberti_rafael@yahoo.com.br

5. Email: jacques@unisc.br