

Vol. 38 (Nº 52) Ano 2017. Pág. 27
Francislaine Suelia dos SANTOS 1; Daniela Dantas de Farias LEITE 2; Rossana Maria Feitosa de FIGUEIRÊDO 3; Alexandre José de Melo QUEIROZ 4
Recebido: 09/06/2017 • Aprovado: 10/07/2017
RESUMO: O objetivo deste trabalho foi determinar as curvas de cinética de secagem da romã nas temperaturas de 50, 60 e 70 °C, ajustar os modelos matemáticos, Aproximação da Difusão, Dois Termos, Page, Henderson e Pabis, Exponencial de Dois Termos, Logarítmico e Thompson aos valores experimentais. O modelo de Page foi selecionado como o mais adequado para predizer o fenômeno de secagem, apresentando R2 > 0,998, menores desvios quadráticos médios (DQM<0,022) e distribuição aleatória dos resíduos em todas as temperaturas estudadas. |
ABSTRACT: The objective of this work was to determine the drying kinetics curves of the pomegranate at temperatures of 50, 60 and 70 °C, adjust the mathematical models, Two Terms, Page, Henderson and Pabis, Exponential of Two Terms, Logarithmic and Thompson to the experimental values. The Page model was selected as the most suitable to predict the drying phenomenon, presenting R2> 0.998, smaller mean square deviations (DQM < 0,022) and random distribution of residues at all temperatures studied. |
A romã (Punica granatum L.) é um fruto advindo de um arbusto ramificado, da família Punicaceae, nativa da região que abrange desde o Irã até o Himalaia (Jardini e Mancini Filho, 2007). No Brasil é bastante consumida principalmente na forma in natura, sendo conhecida popularmente para o uso medicinal. Entretanto, na indústria de alimentos, pode ser utilizada para produzir suco, vinho, licor, geleia, aromatizantes e corante na indústria de cosméticos (Modaresi et al., 2011).
A parte comestível da fruta (polpa) apresenta em sua composição compostos fenólicos como: antocianinas, quercetina, ácidos fenólicos e taninos (Noda et al., 2002). E flavonóides que, extraídos do suco fermentado e do óleo das sementes, apresentaram atividade inibitória das enzimas oxidantes ciclooxigenase e lipooxigenase (Taufner et. al., 2006).
Entretanto, para aumentar a vida útil durante a estocagem e comercialização dos produtos agrícolas, se faz necessário reduzir a quantidade de água do material e consequentemente da sua atividade biológica (Santos et al., 2013). A secagem surge, então, como um dos principais processos utilizados pela indústria, auxiliando na conservação e qualidade dos produtos agrícolas.
A secagem é utilizada com o intuito de reduzir o teor de água até níveis seguros para o armazenamento do produto (Corrêa et al., 2007). Este processo envolve a transferência de calor e massa, influenciando na modificação das atividades biológicas e a estrutura química e física das sementes, dependendo das condições e métodos de secagem adotados (Resende et al., 2010).
A cinética de secagem é uma análise sobre o comportamento da transferência de massa entre o produto e o agente de secagem, e contribui com informações sobre o comportamento do mesmo durante o processo (Siqueira et al., 2012). O estudo da cinética de secagem desperta o interesse de pesquisadores para os mais diversos tipos de produtos. Porém não existem muitos estudos a respeito dos fenômenos que ocorrem durante a secagem da romã.
Logo a secagem da romã é indicada como um meio de aumentar a sua vida útil e como forma de produzir novos produtos. Sendo assim, este trabalho teve como objetivo determinar as cinéticas de secagem da romã (sementes com polpa) em diferentes temperaturas e ajustar diferentes modelos matemáticos aos dados experimentais.
A matéria-prima utilizada foram as romãs (Punica granatum) maduras advindas da cidade de Campina Grande – PB. As frutas foram transportadas adequadamente ao laboratório, onde foram selecionadas manualmente, de forma a eliminar os exemplares que apresentavam danos físicos ou estavam em estádio de maturação inadequado. Procedeu-se a sanitização em água clorada (50 ppm) por 15 minutos, posteriormente, enxague em água corrente.
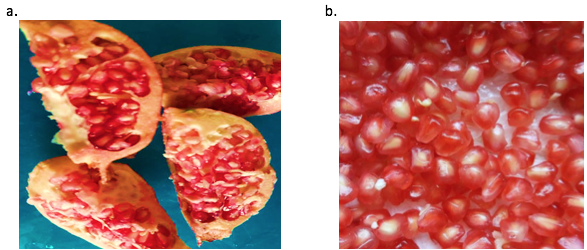
Em seguida os frutos foram cortados diagonalmente em quatro partes (Figura 1a), sendo as sementes com a polpa separadas da casca (Figura 1b). Em seguida as sementes com a polpa (Figura 1b) foram colocadas em bandejas de aço inoxidável com peso padronizado e submetidas à secagem em estufa com circulação forçada de ar nas temperaturas de 50, 60 e 70 °C e velocidade do ar de 1,0 m/s.
Figura 1
Romã: a. cortada em quatro partes; b. sementes com a polpa
As cinéticas de secagem, realizadas em triplicata, foram obtidas através da pesagem das amostras em intervalos regulares, até massa constante. No final das secagens foram determinadas as massas secas e calculadas as razões de umidade das amostras (Eq. 1) e traçadas as curvas da razão de umidade em função do tempo de secagem.
![]() (1)
(1)
Onde:
RX - razão de umidade do produto (adimensional);
X - teor de umidade do produto (base seca);
Xi - teor de umidade inicial do produto (base seca);
Xe - teor de umidade de equilíbrio do produto (base seca).
Os modelos matemáticos apresentados na Tabela 1 foram ajustados às curvas de cinética de secagem da romã (sementes com polpa) através de regressão não linear, pelo método Quasi-Newton, empregando-se o programa computacional Statistica 7.0.
Tabela 1
Modelos matemáticos utilizados para estimar as curvas
de cinética de secagem da romã (sementes com polpa)

RX - razão de umidade do produto, adimensional; k - constantes de secagem;
a, b, c, n, q - constantes dos modelos; t - tempo de secagem (min).
Para avaliar a qualidade dos ajustes dos modelos matemático aos dados experimentais foram avaliados o coeficiente de determinação (R²), o desvio quadrático médio (DQM) (Eq. 9) e a distribuição dos resíduos.
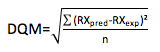 (9)
(9)
Onde:
DQM - desvio quadrático médio;
RXpred - razão de umidade predito pelo modelo;
RXexp - razão de umidade experimental;
n - número de observações.
Têm-se, na Figura 2, os dados experimentais da cinética de secagem da romã (sementes com polpa) nas temperaturas de 50, 60 e 70 °C, expressos através do teor de umidade (% b.u.) em função do tempo de secagem (min).
Figura 2
Curvas de cinética de secagem da romã (sementes
com polpa) nas temperaturas de 50, 60 e 70 °C
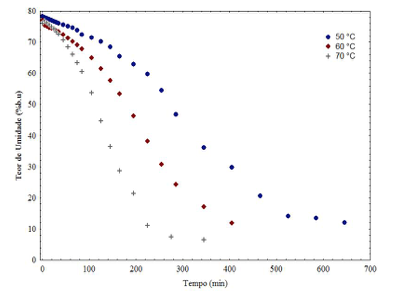
Observa-se a redução do tempo do processo de secagem com o aumento da temperatura, comportamento já esperado uma vez que com a elevação da temperatura do ar de secagem cria-se um maior gradiente de umidade entre o produto e o ar, acarretando em maior taxa de remoção de água, independente do tipo de produto (Sousa et al., 2011). Consequentemente houve a diminuição do teor de umidade com o aumento da temperatura de secagem, comportamento também verificado na secagem de grãos de algaroba (Silva et al., 2012); e das sementes de abóbora (Diógenes et al., 2013).
As secagens da romã (sementes com polpa) foram procedidas durante 645 min na temperatura de 50 °C, 405 min na temperatura de 60 °C e 345 min na temperatura de 70 °C. Costa et al. (2011) verificaram redução nos tempos de secagem com elevação da temperatura nas sementes de crambe (Crambe abyssinica) em estufa com circulação forçada de ar, obtendo tempos de secagem de 20,5; 8,5; 5,0; 5,0 e 2,75 h para as temperaturas de 30, 40, 50, 60 e 70 °C, respectivamente, sendo inferiores ao da romã.
Apresentam-se, na Tabela 2, os parâmetros dos modelos matemáticos de Aproximação da Difusão, Dois Termos, Exponencial de Dois Termos, Henderson e Pabis, Logarítmico, Page e Thompson, ajustados aos dados experimentais das cinéticas de secagem da romã e seus respectivos coeficientes de determinação (R²) e desvios quadráticos médios (DQM).
Tabela 2
Parâmetros dos modelos matemáticos ajustados às curvas de cinética de secagem
da romã (sementes com polpa), coeficientes de determinação (R²), desvios
quadráticos médios (DQM)
Modelo |
Temp. (°C) |
Parâmetros |
R2 |
DQM |
|||||
a |
b |
c |
k |
n |
q |
||||
Aproximação da Difusão |
50 |
-34,132 |
0,9864 |
- |
0,0088 |
- |
- |
0,9986 |
0,0165 |
60 |
-86,475 |
0,9907 |
- |
0,0133 |
- |
- |
0,9978 |
0,0228 |
|
70 |
-179,752 |
0,9950 |
- |
0,9950 |
- |
- |
0,9994 |
0,0129 |
|
Dois Termos |
50 |
0,5093 |
0,5073 |
- |
0,0057 |
- |
0,0057 |
0,9974 |
0,0247 |
60 |
0,5291 |
0,5290 |
- |
0,0071 |
- |
0,0071 |
0,9885 |
0,0516 |
|
70 |
0,5473 |
0,5461 |
- |
0,0112 |
- |
0,0112 |
0,9911 |
0,0479 |
|
Exponencial de Dois Termos |
50 |
9,4506 |
- |
- |
0,0006 |
- |
- |
0,9971 |
0,0261 |
60 |
3,5399 |
- |
- |
0,0018 |
- |
- |
0,9985 |
0,0596 |
|
70 |
5,8845 |
- |
- |
0,0017 |
- |
- |
0,9839 |
0,0644 |
|
Henderson e Pabis |
50 |
1,0166 |
|
- |
0,0057 |
- |
- |
0,9974 |
0,0247 |
60 |
1,0581 |
- |
- |
0,0071 |
- |
- |
0,9845 |
0,0516 |
|
70 |
1,0934 |
- |
- |
0,0112 |
- |
- |
0,9911 |
0,0644 |
|
Logarítmico |
50 |
1,0743 |
- |
-0,0714 |
0,0049 |
- |
- |
0,9990 |
0,0152 |
60 |
1,3001 |
- |
-0,2739 |
0,0045 |
- |
- |
0,9963 |
0,0292 |
|
70 |
1,1930 |
- |
-0,1215 |
0,0089 |
- |
- |
0,9951 |
0,0354 |
|
Page |
50 |
- |
- |
- |
0,0033 |
1,1067 |
- |
0,9985 |
0,0188 |
60 |
- |
- |
- |
0,0011 |
1,3620 |
- |
0,9980 |
0,0216 |
|
70 |
- |
- |
- |
0,0014 |
1,4377 |
- |
0,9997 |
0,0086 |
|
Thompson |
50 |
-0,2574 |
0,2040 |
- |
- |
- |
- |
0,9547 |
0,1025 |
60 |
-0,2746 |
0,2121 |
- |
- |
- |
- |
0,9234 |
0,1306 |
|
70 |
-0,3149 |
0,2518 |
- |
- |
- |
- |
0,9266 |
0,1362 |
|
Verifica-se que os modelos matemáticos testados de Aproximação da Difusão, Dois Termos, Exponencial de Dois Termos, Henderson e Pabis, Logarítmico e Page resultaram em bons ajustes aos dados experimentais das secagens da romã (sementes com polpa) na faixa de temperatura estudada, com R² superiores a 0,97 e baixos valores de DQM. Quanto ao modelo de Thompson o mesmo apresentou um R² médio de 0,93, DQM acima de 0,09 resultados bastante distintos dos demais modelos, considerado não satisfatório para estimar as curvas de cinética do material em estudo.
Observa-se que dentre os modelos testados o melhor ajuste na temperatura de 50 oC foi com o modelo Logarítmico, em razão de ter apresentado o maior coeficiente de determinação (R² = 0,9990), o menor desvio quadrático médio (DQM = 0,0152); na temperatura de 60 oC o melhor modelo recomendado para representar a cinética de secagem da romã foi o de Page; e na temperatura de 70 oC o melhor ajuste foi também com o modelo de Page, apresentando o maior R2 e o menor DQM.
O parâmetro k dos modelos matemáticos de Aproximação da Difusão, Dois Termos e Henderson e Pabis diminuiu com a elevação da temperatura de secagem; no entanto, verifica-se para os modelos Exponencial de Dois Termos, Logarítmico e Page que houve diminuição de k entre as temperatura de 50 e 60 °C e aumento entre 60 e 70 oC. Corrêa et al. (2010) afirmaram que o parâmetro k tende a aumentar com o aumento da temperatura de secagem, pois maiores temperaturas acarretam em maiores taxas de secagem atingindo o teor de umidade de equilíbrio em menor tempo de submissão do produto ao ar de secagem. Diante disso, constata-se comportamento inverso na maioria dos modelos testados para a romã, comportamento semelhante foi verificado por Santos et al. (2013) na secagem da farinha de grãos residuais de urucum, nas temperaturas de 40 a 70 °C.
O parâmetro n do modelo de Page possui um efeito de moderação do tempo e corrige os prováveis erros resultantes da negligência da resistência interna para a transferência de água (Guedes e Faria, 2000). Observa-se que houve aumento do parâmetro n com o aumento da temperatura de secagem. Comportamento semelhante também foi reportado por Reis et al. (2015) na secagem da pimenta bico em diferentes condições de temperatura (40, 50 e 60°C) e velocidade do ar de secagem (1,0; 1,5 e 2,0 m/s).
Quanto ao parâmetro a, dos modelos de Dois Termos, Exponencial de Dois Termos e Henderson e Pabis apresentou aumento com a elevação da temperatura. Comportamento semelhante também foi verificado no ajuste do modelo de Page aos dados experimentais da secagem de grãos de soja, em que houve aumento com a temperatura nos parâmetros a e n deste modelo (Rafiee et al., 2009).
Em relação ao parâmetro b nos modelos Aproximação da Difusão, Dois Termos e Thompson observa-se que houve aumento com a elevação da temperatura de secagem. Sousa et al. (2011) também verificaram este comportamento ao ajustarem as curvas de secagem no nabo forrageiro (Raphanus sativus L.), entre as temperaturas de 30 a 70 °C verificando aumento no parâmetro b com a elevação da temperatura de secagem.
Para a seleção do melhor modelo matematico ajustados aos dados experimentais tambem observou-se a tendência de distribuição de resíduos (Tabela 3) de todos os modelos ajustados as curvas de cinética de secagem da romã (semente e polpa). Gonelli et al. (2011) relataram que um modelo é considerado aceitável se os valores dos resíduos apresentarem distribuição aleatória. Se apresentar distribuição tendenciosa, o modelo é considerado inadequado para representar o fenômeno em questão. A não formação de figuras definidas indica aleatoriedade dos resultados (Santos et al., 2013).
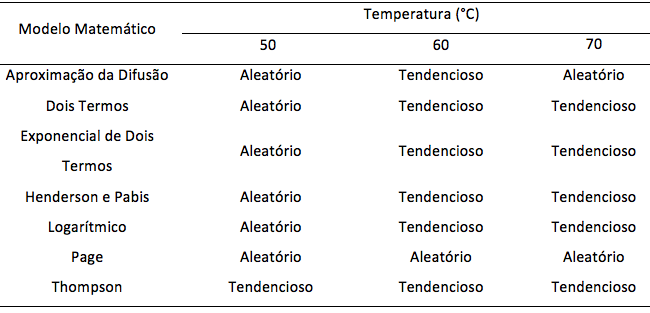
Tabela 3
Tendência de distribuição de resíduos para os modelos ajustados aos dados experimentais
da cinética de secagem da romã nas temperatura de 50, 60 e 70 °C
Modelo Matemático |
Temperatura (°C) |
||
50 |
60 |
70 |
|
Aproximação da Difusão |
Aleatório |
Tendencioso |
Aleatório |
Dois Termos |
Aleatório |
Tendencioso |
Tendencioso |
Exponencial de Dois Termos |
Aleatório |
Tendencioso |
Tendencioso |
Henderson e Pabis |
Aleatório |
Tendencioso |
Tendencioso |
Logarítmico |
Aleatório |
Tendencioso |
Tendencioso |
Page |
Aleatório |
Aleatório |
Aleatório |
Thompson |
Tendencioso |
Tendencioso |
Tendencioso |
Verifica-se que o modelo de Page foi o único modelo com distribuição aleatória dos resíduos em todas as temperaturas estudadas, resultando no melhor ajuste aos dados de secagem da romã. Resultados semelhantes foram reportados por Mendonça et al. (2015) nas curvas de secagem de sementes de andiroba onde o modelo de Page foi o melhor.
Na Figura 3 estão dispostas as curvas experimentais das cinéticas de secagem da romã (semente e polpa) nas temperaturas de 50, 60 e 70 °C, e as curvas ajustadas com o modelo de Page, que foi de modo geral o melhor modelo. Verifica-se que os pontos experimentais ficaram muito próximos das curvas preditas.
Figura 3
Curvas de cinética de secagem da romã (sementes com polpa) nas
temperaturas de 50, 60 e 70 °C ajustadas pelo modelo de Page
As curvas de secagem foram influenciadas pela temperatura, sendo observada redução gradativa nos tempos de secagem a medida que a temperatura do ar de secagem era aumentada. Este comportamento é frequente e foi relatado para vários produtos agrícolas como para a casca do mulungu, resíduo do abacaxi, farinha de grãos residuais de urucum e dos frutos de mamona (Martins et al., 2014; Alexandre et al., 2013; Santos et al., 2013; Goneli et al., 2011). Isso ocorre em razão da maior taxa de remoção de água do produto devido a um maior gradiente de umidade entre o produto e o ar, ocasionado pelo aumento da temperatura (Sousa et al., 2011).
A temperatura exerceu influência sobre o tempo de secagem, onde as romãs (sementes com polpa) secadas nas maiores temperaturas demandaram os menores tempos para o equilíbrio higroscópico.
Dentre os modelos matemáticos ajustados aos dados experimentais da cinética de secagem das sementes de romã, o de Page foi selecionado como o mais adequado para predizer o fenômeno estudado, apresentando na maioria dos casos os maiores valores de R2, os menores desvios quadráticos médios e distribuição dos resíduos aleatória.
Os modelos matemáticos Aproximação da Difusão, Dois Termos, Exponencial de Dois Termos, Henderson e Pabis e Logarítmico, também podem ser utilizados para estimar os dados experimentais da cinética de secagem das sementes de romã, pois resultaram em bons ajustes aos dados experimentais na faixa de temperatura estudada, com R² superiores a 0,98 e baixos valores de DQM.
Alexandre, H. V.; Silva, F. L. H.; Gomes, J. P.; Silva, O. S.; Carvalho, J. P. D.; Lima, E. E. Cinética de secagem do resíduo de abacaxi enriquecido. Revista Brasileira de Engenharia Agrícola e Ambiental, v. 17, n. 6, p. 640-646, 2013.
Corrêa, P. C.; Resende, O.; Martinazzo, A. P.; Goneli, A. L. D.; Botelho, F. M. Modelagem matemática para a descrição do processo de secagem do feijão (Phaseolus vulgaris L.) em camadas delgadas. Engenharia Agrícola, v. 27, n. 2, p. 501-510, 2007.
Corrêa, P. C.; Oliveira, G. H. H.; Botelho, F. M.; Goneli, A. L. D.; Carvalho, F. M. Modelagem matemática e determinação das propriedades termodinâmicas do café (Coffea arabica L.) durante o processo de secagem. Revista Ceres, v. 57, n. 5, p. 595-601, 2010.
Costa, L. M.; Resende, O.; Sousa, K. A.; Gonçalves, D. N. Coeficiente de difusão efetivo e modelagem matemática da secagem de sementes de crambe. Revista Brasileira de Engenharia Agrícola e Ambiental, v. 15, n. 10, p. 1089-1096, 2011.
Diógenes, A. M. G.; Queiroz, A. J. M.; Figueirêdo, R. M. F.; Santos, D. C. Cinética de secagem de grãos de abóbora. Revista Caatinga, v. 26, n. 1, p. 71-80, 2013.
Gonelli, A. L. D.; Corrêa, P. C.; Magalhães, F. E. A.; Baptestini, F. M. Contração volumétrica e forma dos frutos de mamona durante a secagem. Acta Scientiarum. Agronomy, v. 33, n. 1, p. 1-8, 2011.
Guedes, A. M. M.; Faria, L. J. G. Determinação da constante de secagem de urucum (Bixa orellana L.) em secador convectivo de leito fixo. Revista Brasileira de Produtos Agroindustriais, v. 2, n. 1, p. 73-86, 2000.
Jardini, F. A.; Mancini Filho, J., Composição centesimal e perfil dos ácidos graxos de romã (Punica granatum, L. ) cultivada no Brasil, Revista Brasileira de Ciências Farmacêuticas, v. 43, n. 1, 2007.
Martins, J. J. A.; Marques, J. I.; Santos, D. C.; Rocha, A. P. T. Modelagem matemática da secagem de cascas de mulungu. Bioscience Journal, v. 30, n. 6, p. 1652-1660, 2014.
Mendonça, A. P.; Sampaio, P. T. B.; Almeida, F. A. C.; Ferreira, R. F.; Novais, J. M. Determinação das curvas de secagem das sementes de andiroba em secador solar. Revista Brasileira de Engenharia Agrícola e Ambiental, v. 19, n. 4, p. 382-387, 2015.
Modaresi, J.; Nasri, M. H. F.; Rashidi, L.; Dayani, O.; Kebreab, E. Short communication: Effects of suplementation with pomegranate seed pulp on concentrations of conjugated linoleic acid and punicic acid in goat milk. Journal of Dairy Science, v. 94, p. 4075-4080, 2011.
Noda, Y.; Kaneyuki, T.; Mori, A.; Packer, L. Antioxidant activities of pomegranate fruit extract and its anthocyanidins: delphinidin, cyaniding and pelargonidin. J. Agric. Food Chem., Washington, v.50, n.1, p. 166-171, 2002.
Rafiee, S. H.; Keyhani, A.; Sharifi, M.; Jafari, A.; Mobli, H.; Tabatabaeefar, A. Thin layer drying properties of soybean (Viliamz Cultivar). Journal of Agricultural Science and Technology, v. 11, n. 3, p. 289-300, 2009.
Reis, D. R.; Santos, P.; Silva, F. S.; Porto, A. G. Influência das características do ar na cinética de secagem de pimenta variedade bico. Brazilian Journal Food Technology, v. 18, n. 2, p. 146-154, 2015.
Resende, O.; Ferreira, L. U.; Almeida, D. P. Modelagem matemática para descrição da cinética de secagem do feijão Adzuki (Vignaangularis). Revista Brasileira de Produtos Agroindustriais, v. 12, n. 2, p.171-178, 2010.
Santos, D. C.; Queiroz, A. J. M.; Figueirêdo, R. M. F.; Oliveira, E. N. A. Cinética de secagem de farinha de grãos residuais de urucum. Revista Brasileira de Engenharia Agrícola e Ambiental, v. 17, n. 2, p. 223-231, 2013.
Silva, L. A.; Cavalcanti-Mata, M. E. R. M.; Duarte, M. E. M.; Almeida, R. D.; Cavalcanti, R. F. R. M. Cinética da secagem de grãos de algaroba. Revista Brasileira de Produtos Agroindustriais, v. 14, p. 535-542, 2012.
Siqueira, V. C.; Resende, O.; Chaves, T. H. Dryng kinetcs of jatropha seeds. Revista Ceres, v. 59, n. 2, p. 171-177, 2012.
Sousa, K. A.; Resende, O.; Chaves, T. H.; Costa, L. M. Cinética de secagem do nabo forrageiro (Raphanus sativus L.). Revista Ciência Agronômica, v. 42, n. 4, p. 883-892, 2011.
Taufner, C. F.; Ferraço, E. B.; Ribeiro, L. F. Uso de plantas medicinais como alternativa fitoterápica nas unidades de saúde pública de Santa Teresa e Marilândia, ES. Natureza on line, v.4, n.1, p.30-39, 2006.
1. Mestranda em Engenharia Agrícola – Universidade Federal de Campina Grande UFCG/CTRN. suelia_santos@hotmail.com
2. Doutoranda em Engenharia Agrícola – Universidade Federal de Campina Grande UFCG/CTRN. danieladantasfl@gmail.com
3. Professora Titular da Unidade Acadêmica de Engenharia Agrícola – UFCG/CTRN. rossana@deag.ufcg.edu.br
4. Professor Titular da Unidade Acadêmica de Engenharia Agrícola – UFCG/CTRN. alex@deag.ufcg.edu.br