

Vol. 38 (Nº 28) Año 2017. Pág. 7
Letícia MARASCA 1; Steffani Nikoli DAPPER; Claudia Aline de Souza RAMSER; Edson Paulo dos SANTOS 2
Recibido: 26/12/16 • Aprobado: 23/01/2017
RESUMO: O mundo está conectado de forma homogênea e os negócios têm deixado de ser exclusivamente internos no país, alcançando níveis mundiais, através das exportações. O objetivo deste estudo é estimar um modelo não-linear da classe geral ARCH para compreensão dos efeitos da volatilidade da série de exportações brasileiras. Os dados utilizados formam uma série histórica das exportações brasileiras (FOB) em milhões de dólares, com coleta mensal, e se referem ao período de janeiro de 1977 a agosto de 2016, totalizando 476 observações. A metodologia empregada é a da modelagem ARCH. Com base no modelo ajustado, foi possível realizar previsão in sample. O processo gerador da série é um auto regressivo de ordem 2, com uma diferença necessária para tornar a série estacionária, e componente médias móveis de ordem 2, apresentando ainda efeito sazonal no lag 12, e apresentando também heterocedasticidade de ordem 1. |
ABSTRACT: The world is connected homogeneously and businesses are not exclusively nationals, reaching global levels, through the exports. The aim of this study is to estimate a nonlinear model of ARCH general class to understand the effects of the volatility of the Brazilian exports’s series. The data used form a historical series of Brazilian exports (FOB) in millions of dollars, from January 1977 to August 2016, with 476 observations monthly. The methodology employed is the ARCH modeling. Based on the adjusted model, it was possible to perform forecast in sample. The generating process of the series is autoregressive of order 2, with a difference necessary to make the series stationary and 2 moving average parameter, with seasonal effect on lag 12 and heterocedasticity of order 1. |
Atualmente, o mundo está conectado de forma homogênea, não só economicamente, mas em todos os aspectos. Os negócios têm deixado de ser exclusivamente internos no país, para se expandirem e alcançarem níveis internacionais, o que ocorre através da exportação, que é a saída além das fronteiras do país de origem de produtos, bens e serviços.
Segundo Cortiñas Lopez e Gama (p. 190, 2005), as exportações são vendas de serviços ou produtos de uma empresa localizada em um país de origem para outra empresa localizada em outro país.
O objetivo deste estudo é estimar um modelo linear da classe geral ARIMA para prever o comportamento médio da série de exportações do país e um modelo não linear da classe geral ARCH para compreensão dos efeitos da volatilidade da série, uma vez que a oscilação econômica reflete uma oscilação nas exportações.
Este estudo está estruturado em seis sessões: nesta primeira sessão tem-se uma breve introdução; a segunda sessão fornece o referencial teórico; na terceira sessão apresentam-se os procedimentos metodológicos aplicados e os dados utilizados na modelagem; na quarta sessão estão os resultados e as discussões e por fim, na sexta sessão, as conclusões.
Os modelos ARIMA (Modelos Autorregressivos Integrados e de Médias Móveis), foram propostos por Box & Jenkins em 1970 e consistem no ajuste dos modelos a um conjunto de dados, cuja escolha da estrutura dos modelos é baseada nos próprios dados (Morettin & Toloi, 2004).
As séries temporais serão modeladas pelos filtros AR, MA, ARMA ou ARIMA, representados nas equações 1 a 4:

Pela metodologia Box & Jenkins, é necessário que ao modelar a série, esta seja estacionária, o que pode ser comprovado pelos testes de raízes unitárias ADF – Dickley-Fuller Aumentado (1997) e KPSS – Kwiatkowski, Phillips, Schmidt e Shin (1992) (OLIVEIRA, MILACH E CORTE, 2010). No caso da série ser não estacionária, é necessário a aplicação de diferenças para tonar a série estacionária. Geralmente, a primeira diferença estacionariza a média, e a segunda, estacionariza a variância.
A identificação de um modelo provisório, e também a confirmação da estacionariedade da série, será dada através da FAC – Função de Auto Correlação e da FACP – Função de Auto Correlação Parcial, e permitem a posterior estimação dos parâmetros pelo Método dos Mínimos Quadrados Ordinários.
O melhor modelo será escolhido com base nos resíduos gerados por ele (diferença entre o valor real e o valor previsto da série), pois quanto menor o resíduo, mais representativo da série é o modelo escolhido. O que se espera é chegar ao resíduo denominado de ruído branco: média zero, variância constante e não auto correlacionados (BACO, PAIVA E LIMA, 2006).
Outro critério utilizado para identificação do melhor modelo ajustado à série será a minimização dos critérios penalizadores Akaike Information Criterion – AIC (equação 5) e Bayesian Information Criterion – BIC (equação 6), que leva em conta a parcimônia do modelo, ou seja, o modelo com menor número de parâmetros será o modelo melhor ajustado à série (menores valores de AIC e BIC) (LIMA JUNIOR, ET AL., 2013).


A modelagem ARIMA estuda a auto correlação entre os valores da série dentro do período utilizado para a análise. Caso essa auto correlação acontece dentro dos anos de análise, ela é considerada como auto correlação sazonal, com modelos chamados de SARIMA. Esses modelos possuem uma parte não sazonal, com parâmetros (p,d,q) e outra parte sazonal, com parâmetros (P,D,Q)s, sendo s representa a ordem da sazonalidade, sendo estes modelos descritos por SARIMA (p,d,q) (P,D,Q)s (WERNER E RIBEIRO, 2003).
Outra classe de modelos econométricos é a modelagem ARCH (Modelo Auto Regressivo de Heterocedasticidade Condicional), onde a variância dos resíduos não é constante, ocorrendo a heterocedasticidade. Segundo Val (2006), se na estimação do modelo ocorrer a hetorocedasticidade, são gerados parâmetros não eficientes, com erros que afetarão as previsões.
Com a volatilidade variável no decorrer da série, o valor do erro quadrático E(ɛt.ɛt) não é constante, o que torna ideal para modelar esta série os modelos heterocedásticos, que vão além da modelagem ARIMA, modelando o erro quadrático encontrado (ruído branco) (ARÊDES, 2008).
Na modelagem ARCH, a variância do erro et, depende de ![]() , ocorrendo auto correlação na variância dos erros de previsão (VASCONCELLOS, 2007).
, ocorrendo auto correlação na variância dos erros de previsão (VASCONCELLOS, 2007).
Um modelo ARCH, segundo Morettin (2008) pode ser representado pela equação:

A modelagem foi realizada com um banco de dados retirado do Instituto de Pesquisa Econômica Aplicada – IPEA, e corresponde ao total de exportações do Brasil (FOB) em milhões de dólares, coletados mensalmente, iniciando-se em janeiro 1977 e se encerrando em agosto 2016, com um total de 476 observações.
As etapas a serem seguidas na metodologia serão as da metodologia Box & Jenkins, descritas a seguir:
Verificar a estacionariedade da série, utilizando-se, para isso, os testes de raízes unitárias ADF e KPSS;
Identificar os filtros que serão utilizados (AR, MA, ARMA, ARIMA, SARIMA ou ARCH) e suas defasagens, através dos gráficos da FAC e da FACP;
Logo após a identificação do filtro, realizar-se-á a estimação do modelo, por meio do Método da Máxima Verossimilhança;
Pelos critérios penalizadores AIC e BIC, será realizada a investigação dos resíduos do modelo, definindo assim, o melhor modelo ajustado entre os modelos concorrentes. A previsão será realizada com o melhor modelo ajustado à série, e também serão calculadas as estatísticas de previsão: MAPE, U-Theil e EQM.
Definido o melhor modelo ajustado à série de dados, seus resíduos quadráticos serão modelados pela modelagem ARCH, onde etapas análogas ao procedimento ARIMA serão utilizadas.
Para a modelagem dos dados foi utilizado o software Eviews 9 S.V.
O bando de dados coletado para o estudo forma uma série histórica das exportações brasileiras, com coleta mensal, totalizando 476 observações.
Com a inspeção gráfica da série original, pode-se observar o comportamento da série das exportações brasileiras, Figura 1, observa-se que a mesma possui tendência crescente, e pode-se perceber que a série é não estacionária. A partir disso, a série necessitará de uma diferença para se tornar estacionária, Figura 2, sendo possível, com isso, a estabilidade dos parâmetros estimados.
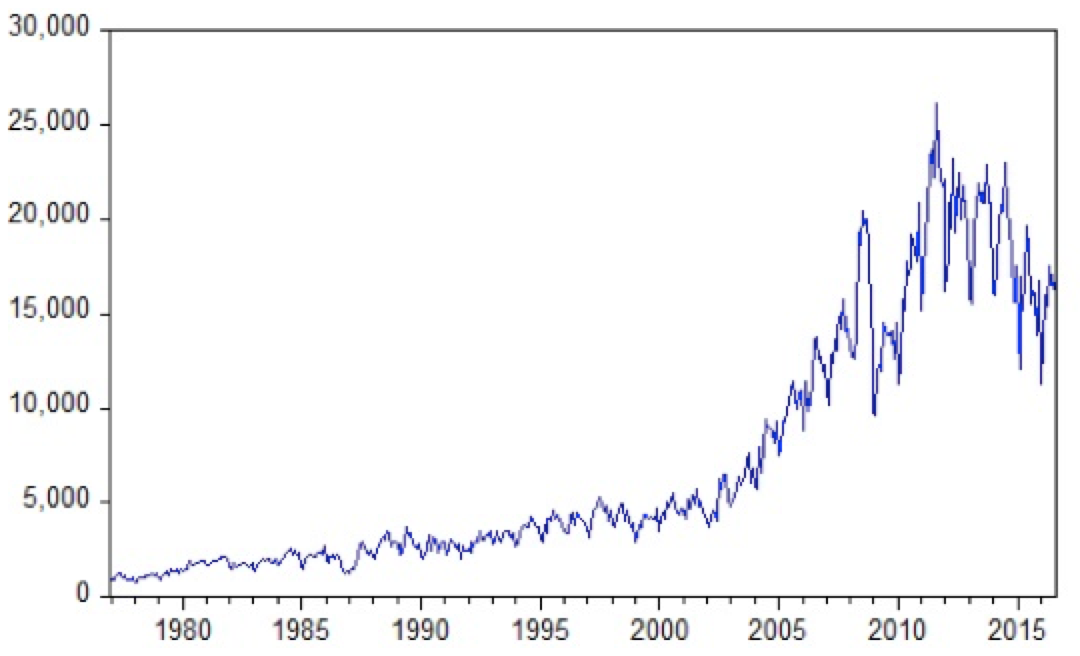
Figura 1: Série Histórica das Exportações Brasileiras.
Ainda com a observação gráfica da Figura 1, pode-se verificar que a série apresenta sinais de volatilidade e de assimetria. Estes sinais de assimetria indicam que esses choques externos impactam na série, o que será comprovado posteriormente, com a utilização da modelagem ARCH.
Observando graficamente a série em estudo, percebe-se que a mesma teve um crescimento gradual, desde o início das observações, em 1977, até o ano de 2003. Entre 2003 e 2008, este cresimento se tornou mais acentuado. Após o ano de 2008, a série começou a apresentar picos crescentes e vales, o que demontra que a série se tornou bastante instável após este período, fato resultante da grande crise econômica internacional enfrentada mundialmente no ano de 2008, que teve seus reflexos sentidos somente a partir do ano seguinte. Essa instabilidade, que pode ser encarada como um cluster de volatilidade, sugere a aplicação da modelagem ARCH.
Na Figura 2, pode-se observar a série orginal e a série em primeiras diferenças.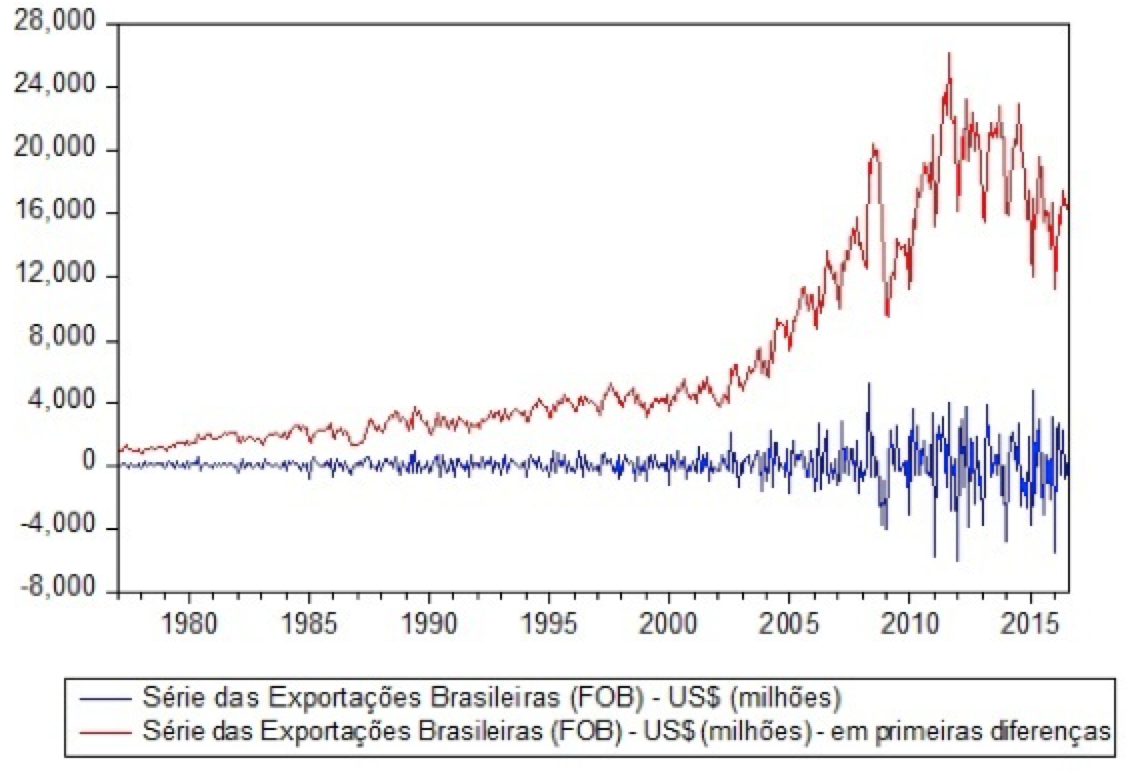
Figura 2: Série original das exportações brasileiras e série em primeiras diferenças.
A série histórica das exportações brasileiras torna-se estacionária após a aplicação de uma diferença (d=1).
Para a comprovação da estacionariedade da série e a verificação de um possível modelo, faz-se a FAC e a FACP, conforme Figura 3, para escolha da classe de modelos que melhor se ajusta na representação ARIMA (p,d,q).
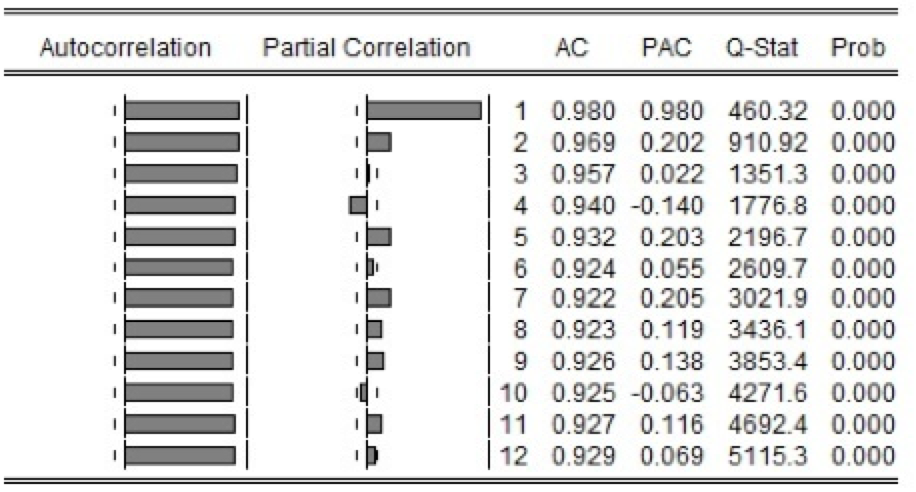
Figura 3: FAC e FACP da série original.
Observando a Figura 3, percebe-se que a FAC não decai para zero, o que demonstra a não estacionariedade da série, e pela FACP, o modelo sugerido seria um auto regressivo.
Os testes ADF e KPSS são aplicados para determinar o grau de estacionariedade da série, conforme Tabela 1.
Tabela 1 - Resultados apresentados pelos testes ADF e KPSS
ADFª |
KPSSb |
|
Série em nível |
-0.708661 |
2.231172 |
Série 1ª diferença |
-5.153465 |
0.123119 |
Fonte: Elaborado pelos autores.
Notas:
a Valores críticos de MacKinnon (1996): -3.493.129 (1%); -2.888.932 (5%) e -2.581.453 (10%).
b Valores críticos de Kwiatkowski-Phillips-Schmidt-Shin(1992, Table 1): 0.739 (1%); 0.463 (5%) e 0.347 (10%).
Os testes corroboram que a série é não estacionária em nível, isto é, I(1).
A escolha pelo melhor modelo foi baseada nos menores valores de AIC e BIC pela minimização dos critérios penalizadores, com parâmetros e estatísticas que podem ser observados conforme Tabela 2.
Tabela 2 – Melhor modelo representativo da Série de Exportações Brasileiras
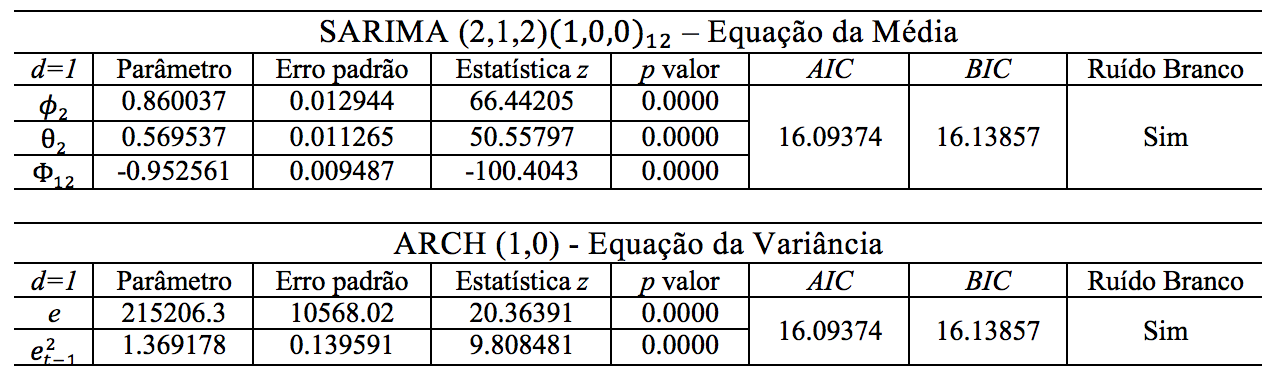
Fonte: Elaborado pelos autores.
O melhor modelo que se ajustou à série é o modelo SARIMA (2,1,2)(1,0,0)12 – ARCH (1).
Na Tabela 2 estão apresentados os parâmetros e estatísticas do melhor modelo ajustado à série, que além de apresentar em seus resíduos as características de ruído branco, apresentou ainda as melhores estatísticas para os critérios penalizadores AIC e BIC.
O modelo selecionado indica que as exportações brasileiras apresentam um comportamento auto regressivo de ordem 2, onde o mês atual será influenciado por 2 períodos anteriores, com fator de influência positivo (0.860037), apresentando assim crescimento nas exportações. Foi captado também um efeito sazonal de 12 meses, com parâmetro sazonal negativo (-0.952561), mostrando um declínio com valor superior à dependência mensal. Em relação ao modelo ARCH, a variância dos resíduos está representada pelo parâmetro ![]() (1.369178), revelando um valor bastante alto, indicando uma queda nos próximos períodos, e esta instabilidade representa mudanças que ocorrerão na média das exportações brasileiras no futuro.
(1.369178), revelando um valor bastante alto, indicando uma queda nos próximos períodos, e esta instabilidade representa mudanças que ocorrerão na média das exportações brasileiras no futuro.
O exame dos resíduos se deu através da FAC e da FACP oriundos do modelo, e estes apresentam-se não auto correlacionados, sem apresentar informações adicionais ao modelo, conforme Figura 4.
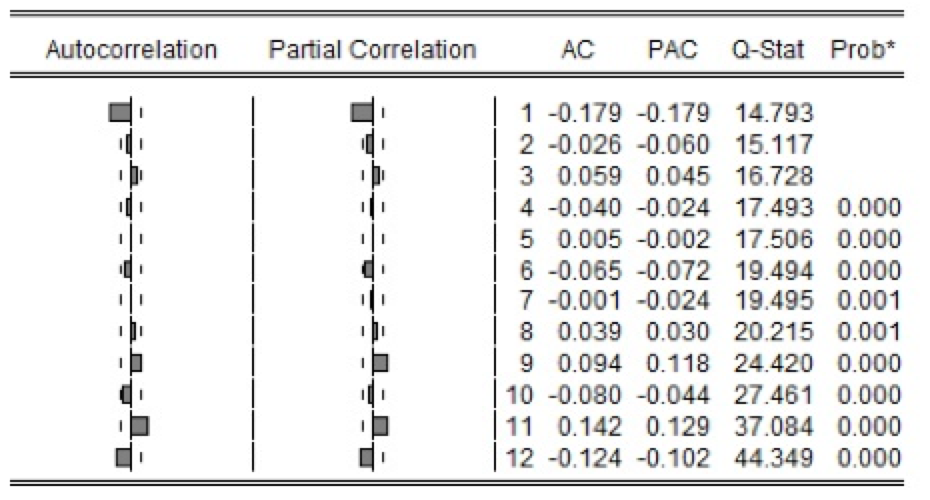
Figura 4: FAC e FACP dos resíduos oriundos do melhor modelo ajustado à série.
Segundo os critérios de validação, o modelo foi adequado, então foram realizadas previsões in sample, para verificar o comportamento futuro da série, conforme Figura 5.
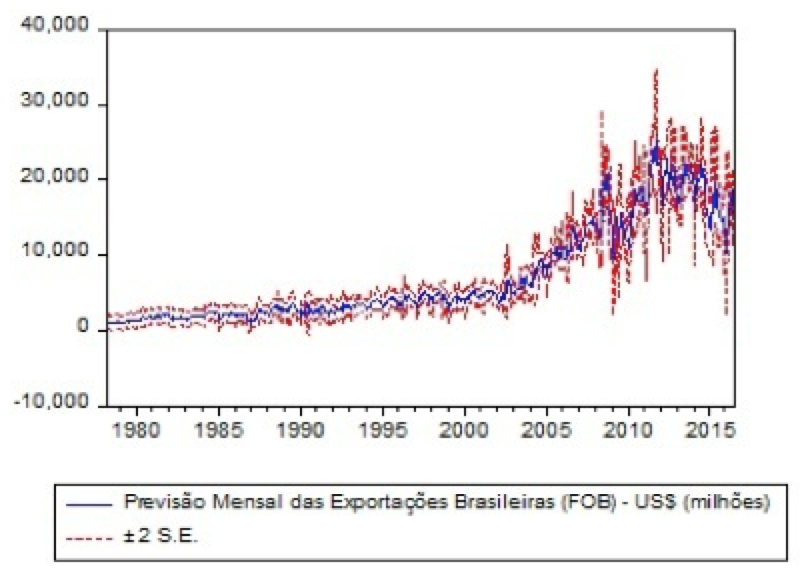
Figura 5: Previsão Mensal das Exportações Brasileiras.
Esta previsão, observada na Figura 5, está de acordo com a realidade, pois o país está passando por uma grave crise econômica e política, sendo assim, as exportações brasileiras tendem a continuar em queda.
As estatísticas de previsão foram realizadas para verificar a adequação dos modelos e os valores encontram-se dentro do esperado. Para a estatística U-THEIL, o valor esperado é o mais próximo de zero, com valores variando de 0 a 1 para uma previsão adequada, e o valor encontrado foi 0.891301. O MAPE é a estatística mais utilizada, e considera os erros em termos percentuais, o valor da estatística gerado é 8.611283 e para o EQM o resultado encontrado foi 959.8217.
Observa-se o gráfico do comportamento da volatilidade estimada pelo modelo linear SARIMA(2,1,2) – ARCH(1) na Figura 6, onde a volatilidade da série permanece estável desde o início das observações até o ano de 2002, se tornando após este ano instável, se mantendo assim até os dias atuais.
O parâmetro ![]() do modelo ARCH tem valor 1.369178, o que mostra que a volatilidade da série apresenta um alto valor, o que significa que as exportações brasileiras estão bastante instáveis, com um alto grau de incerteza nesse ramo de atividades.
do modelo ARCH tem valor 1.369178, o que mostra que a volatilidade da série apresenta um alto valor, o que significa que as exportações brasileiras estão bastante instáveis, com um alto grau de incerteza nesse ramo de atividades.
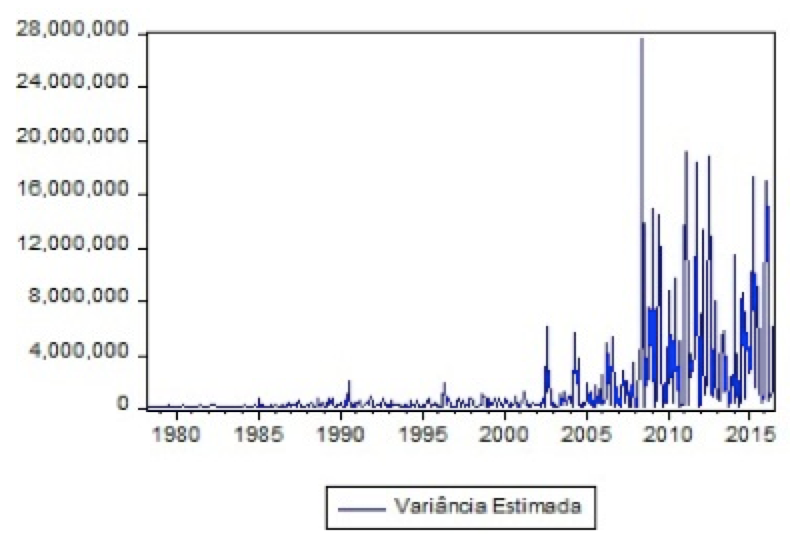
Figura 6 – Gráfico do comportamento da volatilidade estimada pelo modelo linear – SARIMA(2,1,2)(1,0,0)12 – ARCH(1).
Com isso, percebe-se que o modelo está apto para realização de previsões, pois apresenta todos os requisitos necessários para um modelo adequado, com seus valores previstos dentro do intervalo de confiança de dois desvios-padrões, trazendo bases científicas para as decisões que serão tomadas com base no modelo.
O processo gerador da série é um auto regressivo de ordem 2, com uma diferença necessária para tornar a série estacionária, e componente médias móveis de ordem 2, apresentando ainda efeito sazonal no lag 12, e também heterocedasticidade de ordem 1.
Com base no modelo ajustado, foi possível realizar previsões in sample. Este estudo possibilitou a verificação do comportamento da média condicional, representado pelo modelo ARIMA (Modelos Auto Regressivos Integrados de Média Móvel) e também o comportamento da variância condicional à média do processo, com a utilização da modelagem ARCH (Modelos Auto Regressivos Condicionais a Heterocedasticidade).
A previsão da série continua com um decaimento, e este fato é corroborado com as exportações do país, que continuam em queda. Assim, a metodologia empregada foi eficaz em capturar os movimentos da série de exportações do Brasil.
ARÊDES, Alan Figueiredo de; PEREIRA, Matheus Wemerson Gomes. Potencialidade da utilização de modelos de séries temporais na previsão do preço do trigo no estado do Paraná. Revista de Economia Agrícola, vol. 55, n. 1, p. 63-76, jan./jun. 2008.
BACO, Samuel Bozzi; PAIVA, Anderson Paulo; LIMA, Renato da Silva. Sistemas de previsão de demanda: aplicação em uma fábrica de anéis de pistão automotivos. In: XIII SIMPEP. Bauru / SP. Novembro / 2006.
CORTIÑAS LOPES, José Manuel; GAMA, Marilza. Comércio Exterior Competitivo. 2. ed. São Paulo: Lex Editora, 2005.
IPEA – Instituto de Pesquisa Econômica Aplicada. Disponível em: http://www.ipea.gov.br/portal/. Acesso em: agosto / 2016.
LIMA JUNIOR, Afonso Valau de; REZER, Fernanda; SENNA, Viviane de; SOUZA, Adriano Mendonça; ZANINI, Roselaine Ruviaro. Aplicação da metodologia Box e Jenkins na modelagem e previsão da série das despesas do governo com o Programa Bolsa Família. In: Anais da III SEMANÍSTICA: Semana Acadêmica da Estatística da UFRGS e STATISTICS 2013 (Ano Internacional da Estatística 2013). Porto Alegre, outubro / 2013.
MORETTIN, Paulo Alberto (2008). Econometria Financeira: um curso em séries temporais financeiras. 1. ed. São Paulo: Blucher.
MORETTIN, Pedro Alberto; TOLOI, Clélia Maria de Castro (2004). Análise de Séries Temporais. São Paulo: Edgard Blücher.
OLIVEIRA, Marta Olivia Rovedder de; MILACH, Felipe Tavares; CORTE, Vitor Francisco Dalla. Aplicação dos Modelos ARMA na Previsão de Vendas, 2010.
VAL, Vanessa da Costa; CORRÊA, Vanessa Petrelli. Volatilidade dos fluxos de capitais do balanço de pagamentos brasileiro: uma análise por meio do modelo ARCH (Modelo Auto-Regressivo com Heterocedasticidade Condicional). In: XXXIV ENCONTRO NACIONAL DE ECONOMIA da ANPEC – ASSOCIAÇÃO NACIONAL DOS CENTROS DE PÓS-GRADUAÇÃO EM ECONOMIA. 2006.
WERNER, Liane; RIBEIRO, José Luis Duarte. Previsão de demanda: uma aplicação dos modelos Box-Jenkins na área de assistência técnica de computadores pessoais. G&P – Gestão & Produção, vol. 10, n. 1, p. 47-67, abr. 2003.
VASCONCELLOS, Rui Marcos Grombone de. Reconstrução de espaços de estados aeroelásticos por decomposição em valores singulares. 2007. 127 f. Dissertação (Mestrado em Aeronaves) – Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos.
1. Email: leticiamarasca@yahoo.com.br
2. Graduado em Psicologia pela Universidade Regional Integrada do Alto Uruguai e das Missões, Campus de Santo Ângelo / RS / Brasil