

Vol. 38 (Nº 08) Año 2017. Pág. 1
Quintiliano Siqueira Schroden NOMELINI 1; Eric Batista FERREIRA 2; Denismar Alves NOGUEIRA 3; Anselmo Afonso GOLYNSKI 4; Adelmo GOLYNSKI 5; Thacyo Euqueres de VILLA 6
Recibido: 31/08/16 • Aprobado: 18/09/2016
3. Procedimentos metodológicos
4. Análise e discussão dos resultados
RESUMO: Neste trabalho foram realizadas modelagens univariada e multivariada de uma das principais commodities que compõem o agronegócio brasileiro, soja, utilizando técnicas de séries temporais. Objetivando a previsão da produção de soja, óleo de soja, área cultivada e produtividade além disso com a modelagem multivariada para estabelecer relações de dependência entre a produção de soja e seus derivados: área, produtividade e produção de óleo, que possam auxiliar gestores a planejar volume de estoque, produção, importação e exportação e ainda investimentos no setor. Conclui-se que as previsões para safra 2014/15 foi melhor pelos modelos univariados em que a produção prevista foi de 87,6, 7.224,13, área de 31,3 e produtividade 3034,6. |
ABSTRACT: In this work we performed univariate and multivariate modeling of one of the main commodities that form the Brazilian agribusiness, soybeans using time series techniques. Aiming to forecast soybean production , soybean oil , acreage and productivity in addition to multivariate modeling to establish dependency relationships between the production of soybeans and their derivatives area , productivity and production of oil , which can help managers plan volume of inventory, production , import and export and also investments in the sector . It is concluded that the forecasts for 2014/15 crop was better by univariate models where the estimated production was 87.6, 7224.13, area 31.3 and productivity 3034.6. |
O Brasil com um clima diversificado, chuvas regulares, energia solar abundante e quase 13% de toda a água doce disponível no planeta, tem 388 milhões de hectares de terras agricultáveis férteis e de alta produtividade, dos quais 90 milhões ainda não foram explorados. Assim, o agronegócio é, hoje, a principal locomotiva da economia brasileira e responde por um em cada três reais gerados no país (Brasil, 2009).
Por qualquer ângulo que se analise o mercado, o tamanho que o Brasil adquiriu no campo do agronegócio é impressionante. Até 2015, a participação no mercado internacional de soja deve crescer dos atuais 36% para 46%. A taxa de crescimento demográfico mundial estimada em 30% até 2020, proporcionada em sua maior parte por China e Índia, exigirá um impulso grande no aumento da produção de alimentos. O Brasil é a nação que tem as melhores condições para suprir essa necessidade (Seibel, 2007).
No Brasil, a principal fonte de óleo vegetal é a soja. O caroço de algodão, girassol, mamona e a palma participam com uma pequena parcela desse mercado. Osaki & Batalha (2011), observou que a soja foi a principal oleaginosa esmagada nas unidades agroindustriais do Brasil, em 2006, sendo processada em 83% das unidades.
Atualmente, o mercado mundial de óleo vegetal é composto principalmente por produtos obtidos em quatro oleaginosas: palma, soja, colza e girassol. Em 2014, a produção mundial do óleo vegetal foi de 495,5 milhões de toneladas, aumentando 7% em relação ao ano de 2013. Os óleos de palma e de soja atendem 60% do mercado de óleo vegetal do mundo. Os óleos de colza e de girassol representam 15% e 9%, respectivamente, do mercado mundial (USDA, 2015).
Organizações públicas e privadas necessitam de rumos bem definidos. Precisam também saber que caminhos seguir para direcionar seus esforços e recursos, num futuro próximo e de longo prazo. Essa visão prospectiva não é estática, mas exige redirecionamentos periódicos, em face de mudanças no ambiente externo. Essa diretriz aplica-se, também, ao Ministério da Agricultura, visando o desenvolvimento sustentável do agronegócio brasileiro (Contini et al., 2006).
A previsão de produção das commodities favorece a tomadas de decisões, no sentido de planejar o volume de estoque para o consumo interno, exportações e produção de biodiesel, direcionar produtores no tamanho da área plantada, nos gastos com novas tecnologias, aumento de produtividade, auxiliar organizações públicas nas necessidades de investimento à agricultura, entre outros.
Existem várias fontes que fornecem informações de dados históricas ao longo do tempo de muitas commodities, inclusive da produção de soja. Os estudos dessas séries históricas que irão auxiliar nas tomadas de decisões, e as estimativas de valores futuros está incluída nesses estudos.
Segundo Morettin & Toloi (2006), uma série temporal é qualquer conjunto de observações ordenadas no tempo. Os modelos utilizados para descrever séries temporais são descritos por leis probabilísticas e a construção de um modelo adequado depende de vários fatores, tais como o comportamento do fenômeno ou o conhecimento prévio que se tem de sua natureza e do objetivo da análise. Outra questão importante é a existência de métodos apropriados de estimação e escolha de técnicas que melhor modelem tais fenômenos, com rigor aos critérios estatísticos desses modelos. Existem várias empresas de consultoria focada na análise do agronegócio e vários outros profissionais dessa área, que muitas das vezes deixam em segundo plano esse rigor estatístico por consequência toma-se decisões com base em análises que agregam grandes margens de erros.
Devido a importância do agronegócio na economia do país justifica-se a aplicação de técnicas estatísticas para o estudo das series históricas da produção brasileira de commodities do agronegócio a partir de inferência clássica. Assim, ferramentas de modelagem univariada e multivariada como a utilização de técnicas de séries temporais pode ser aplicado ao banco de dados de produção de soja e seus derivados. Sendo a finalidade da modelagem univariada a previsão da produção de soja, óleo, área e produtividade e a modelagem multivariada para estabelecer relações de dependência entre a produção de soja e seus derivados: área, produtividade e produção de óleo, que possam auxiliar gestores a planejar volume de estoque, produção, importação e exportação e ainda investimentos no setor.
Uma série temporal é um conjunto de observações coletadas de forma sequencial, ao longo do tempo. A dependência entre as observações é o que caracteriza as aplicações das técnicas de séries temporais, já que as metodologias estatísticas clássicas, para serem aplicadas, exigem independência dos dados. Vale ressaltar que, além do tempo, uma série pode ser função de outra variável, como, por exemplo, espaço, profundidade, etc.
A análise de uma série temporal pode ser feita no domínio do tempo ou no domínio da frequência, sendo os modelos propostos, respectivamente, paramétricos e não-paramétricos.
O objetivo da análise em séries temporais é a construção de modelos com propósitos determinados, tais como: investigar o mecanismo gerador da série temporal, fazer previsões de valores futuros, descrever o comportamento da série e procurar periodicidades relevantes nos dados.
Conforme Morettin e Toloi (2006), os modelos utilizados para descrever séries temporais são processos estocásticos, controlados por leis probabilísticas. Um processo estocástico é definido como sendo uma coleção de variáveis aleatórias sequenciadas no tempo e definidas em um conjunto de pontos T, que pode ser contínuo ou discreto. A variável aleatória no tempo t é denotada por Zt, em que t = 0, ±1, ±2, ...,T .
Uma das suposições mais frequentes que diz respeito a uma série temporal é a de que ela é estacionária, ou seja, ela se desenvolve no tempo aleatoriamente ao redor de uma média constante, repetindo alguma forma de equilíbrio estável. Existem, tecnicamente, duas formas de estacionaridade: fraca (ou ampla, ou de segunda ordem) e estrita (ou forte). A estacionaridade forte é uma propriedade muito exigente e, em geral, de difícil verificação. Assim, faz sentido definir um conceito de estacionaridade baseado nos momentos de uma série temporal, mais precisamente nos momentos de primeira e segunda ordens. Isto é dado pela estacionaridade fraca.
Morettin & Toloi (2006) de nem um processo estocástico como sendo fracamente estacionário ou estacionário de segunda ordem se:

Esta definição confirma que um processo estocástico fica bem descrito por meio das funções média, variância e autocovariância.
A função de autocovariância (facv) é a covariância entre Zt e Zt-k separados por k intervalos de tempo ou k lag's:
![]()
Se temos uma série real, o estimador amostral aproximadamente não-tendencioso (para grandes amostras) da autocovariância é dado por:

As funções de autocovariância e autocorrelação são importantes para o estudo descritivo da série, em que se pode verificar se a série é estacionária. Para facilitar essa investigação constrói-se o correlograma, que é um gráfico de barras das medidas correlações estimadas. A partir deste gráfico pode-se associar certos padrões à série temporal, como por exemplo, variações sazonais e tendências.
O ponto chave da análise de uma série temporal é a construção do modelo e este é probabilístico dada a incerteza presente nas variáveis em estudo, deve ser parcimonioso, isto é, o mais simples possível porém com grau de explicação satisfatório, o modelo dever permitir o entendimento da série e o processamento de informações para realizar previsões ou verificar hipóteses sobre valores futuros.
Há vários tipos de modelos utilizados em estudos de séries temporais estacionária dentre eles os lineares autorregressivos de médias móveis (ARMA) que podem ser subdivididos em dois outros grupos os autorregressivos (AR) e de médias móveis (MA). Estes são os principais modelos de Box-Jenkins (Morettin & Toloi; 2006) para estimação e previsão de séries temporais.
Uma decomposição clássica de séries temporais permite que a série {Zt, t=1,2,...,N} seja escrita como uma soma ou multiplicação de componentes não observáveis, como em Zt = Tt + St + at e Zt = TtStat, em que Tt é a tendência, St é a sazonalidade e at é a componente aleatória de média zero e variância constante.
Para Morettin & Toloi (2006), a tendência pode ser entendida como aumento ou diminuição gradual das observações ao longo do tempo, a sazonalidade indica possíveis atuações ocorridas sempre em períodos menores ou iguais a doze meses e a componente aleatória que mostra oscilações aleatórias irregulares.
Segundo Morettin & Toloi (2006), o principal interesse em considerar estes modelos ou estas decomposições é estimar a sazonalidade St e a tendência Tt, pois estas duas componentes estão intrinsicamente ligadas e, conforme Pierce (1979), a influência da tendência sobre a componente sazonal pode ser muito forte e estas componentes fazem com que a série não atinja seu estágio estacionário, condição exigida na metodologia de ajuste dos modelos de Box e Jenkins.
Dentre os diversos métodos e modelos de previsão existentes, destacam-se os modelos de Box e Jenkins, cuja metodologia consiste em ajustar modelos auto-regressivos integrados de médias móveis, ARIMA(p, d, q), a um conjunto de dados. Tais modelos se caracterizam, ainda, por serem simples e parcimoniosos; as previsões são bastante precisas, comparando-se favoravelmente com os demais métodos de previsão. Se classificam em modelos lineares estacionários e não-estacionários.
O nome Auto-Regressivo se deve ao fato de que Zt no instante t é função dos Z's nos instantes anteriores a t. Um modelo auto-regressivo de ordem p, AR(p) é escrito em função de seus valores passados e do ruído branco. É denotado por:
![]()
Já o nome Médias Móveis vem do fato que Zt é uma função soma algébrica ponderada dos at que se movem no tempo. O processo de médias móveis é uma combinação linear de ruídos brancos ocorridos no período presente e no período passado da seguinte forma:
![]()
Os modelos auto-regressivos e de médias móveis são uma combinação linear dos modelos auto-regressivos com médias móveis, podendo, então, serem escritos da forma:
![]()
Grande parte das séries encontradas na prática apresenta alguma forma de não-estacionaridade e, como a maioria dos procedimentos utilizados em séries temporais é para séries estacionárias, é necessário tomar um número d de diferenças finitas para atingir este estágio. Quando isso é possível, tem-se um caso de séries não-estacionárias homogêneas ou séries portadoras de raízes unitárias. Os modelos usados para séries com este comportamento são os modelos ARIMA e SARIMA.
Após identificar a ordem e estimarem-se eficientemente os parâmetros de um modelo, é necessário verificar se ele representa os dados de maneira adequada. Esta verificação é feita pelo teste da autocorrelação residual e pelo teste de Box-Pierce.

O erro de previsão é definido por:

Vários modelos podem ser identificados para descrever uma série, mas existem critérios para escolha do melhor modelo de acordo com o objetivo do ajuste. Dentre diversos critérios, têm-se o critério de informação de Akaike (AIC) e o critério do erro quadrático médio de previsão (EQMP).
A multidimensionalidade dos dados será abordada através da Análise de Clusters, na identificação de agrupamentos (no espaço e no tempo) classificando e reduzindo as variáveis em estudo, assim como pelos métodos de Análise Fatorial e Análise em Componentes Principais de modo a que os fatores latentes identifiquem as covariáveis (naturais e antropogénicas) e as possíveis fontes ou origens que explicam uma parte significativa da variabilidade dos dados.
A dimensão temporal dos dados é incorporada através da modelação e previsão das séries temporais (por aplicação da metodologia clássica de Box & Jenkins, assim como outras, nomeadamente abordagens não paramétricas). Este estudo permitirá desenvolver técnicas para identificar tendências e padrões de evolução das séries e desenvolver critérios para a sua detecção tão importantes na avaliação e identificação dos processos subjacentes à produção e gestão dos recursos naturais.
Pretende-se estudar modelos de séries temporais abordando essencialmente o problema de estimação de estruturas de correlação adequadas, por forma a desenvolver modelos de estimação/previsão para as variáveis de interesse (modelos motivados para a modelação de dados reais) e estudar diferentes critérios para quantificar o poder explicativo dos modelos propostos e a sua capacidade de serem utilizados para a previsão (análise de diagnóstico).

As séries históricas das safras de 1977/78 a 2013/14 para área, produção, produtividade e produção de óleo de soja foi obtida por meio do Departamento de Agricultura dos Estados Unidos da América (USDA, 2015), foi avaliada via teoria de Box e Jenkins (Morettin & Toloi, 2006), além dessa modelagem outros métodos utilizados foram o ajuste da tendência a partir dos modelos linear, quadráticos e Alisamento Exponencial de Holt (AEH).
Para verificar a existência ou não de tendência na série além da inspeção visual das funções de autocorrelações foi realizado o teste do sinal de Cox-Stuart. Segundo Morettin & Toloi (2006), é possível o uso de testes estatísticos de hipóteses para verificar se existe tendência na série. Vários testes podem ser adotados, mas aqui se considerará somente o teste do sinal (Cox-Stuart), o qual se baseia em agrupar as observações em pares. A cada par (Zi, Zi + c) associa o sinal '+', se Zi < Zi + c e o sinal '-', se Zi > Zi + c, eliminando os empates, para c = n/2, em que n é o número de observações da série e Zi é a observação (i = 1,...,n). Se a probabilidade de sinais '+' for igual à probabilidade de sinais '-'; não existe tendência, caso contrário existe tendência. Para T > n-t existe tendência, em que T é o número de sinais positivos e t é encontrado numa tabela de distribuição binomial, com parâmetros p = 1/2 e n, para um dado nível a, se n ≤ 20 e para n>20, pode-se usar distribuição normal em que o n é o número de pares. A periodicidade foi verificada pela análise espectral do periodograma.
Um teste utilizado para verificar se o resíduo é independente e identicamente distribuído, isto é, se o resíduo é um ruído branco, é o teste de Box e Pierce, Priestley (1989), o qual é baseado nas k primeiras autocorrelações, ![]() , dos resíduos. Para um processo ARIMA (p, d, q), se o modelo ajustado é apropriado, então a estatística do teste é:
, dos resíduos. Para um processo ARIMA (p, d, q), se o modelo ajustado é apropriado, então a estatística do teste é:
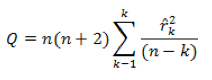
com distribuição aproximadamente qui-quadrado (χ2). A hipótese de ruído branco é aceita para um Q < χ2 com (k - p - q) graus de liberdade, em que k é o número de "lags", p é a ordem da parte auto-regressiva e q a ordem da parte de médias móveis.
Morettin & Toloi (2006) comentam que, para testar se uma série é ruído branco, ou seja, constituída de observações independentes identicamente distribuídas, basta construir o correlograma (gráfico da função de autocorrelação) e o seu intervalo de confiança. As correlações (ou melhor 95% delas) deverão estar dentro deste intervalo de confiança.
A escolha do melhor modelo foi realizada com base no critério de informação de Akaike (AIC) e Erro Quadrático Médio de Previsão (EQMP), quanto menor melhor é o modelo. Além destes critérios calculou-se o MAPE, que avalia o desempenho dos ajustes, quanto menor seu valor menor é o erro percentual e consequentemente melhor o ajuste.
Para o estudo univariado foram avaliados modelos do tipo:

As análises estatísticas foram implementadas no software R (R Core Team, 2015) pacote forecast.
Foi realizado o ajuste de modelos univariado para a série de produção de soja, área de produção, produtividade e produção de óleo de soja, sendo que na Figura 1a1-a4 é apresentado os gráficos da série original. Visualmente, pode-se observar a presença da componente tendência em todos as variáveis. Observa-se na Figura 1b1-b4, que a segunda diferença das séries foi suficiente para eliminar a tendência.
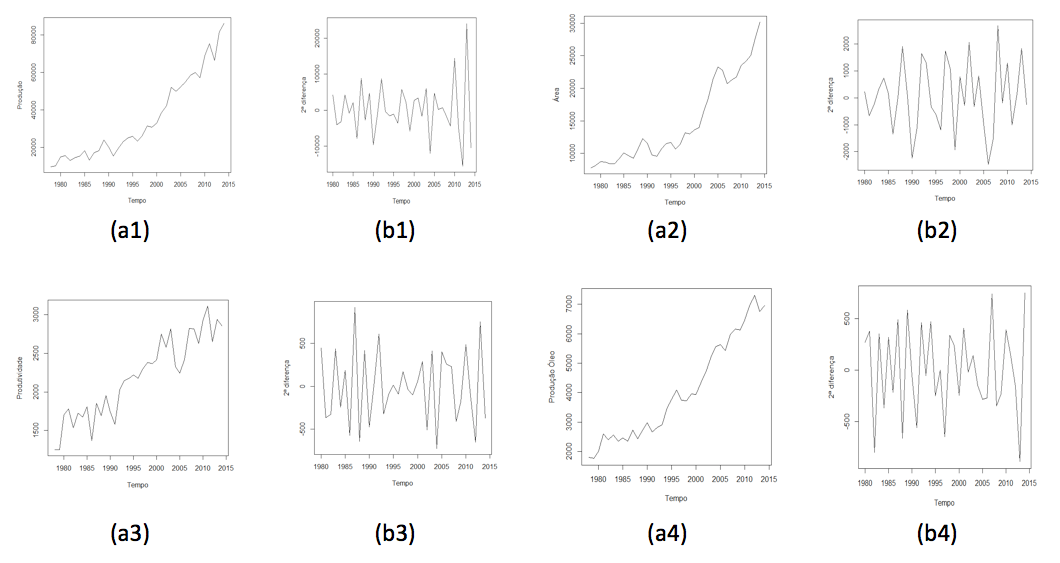
Figura 1. Representação gráfica da série original (a) e diferenciada (b) da produção,
área de produção, produtividade e produção de óleo anual
de soja no Brasil, das safras de 1977/78 a 2013/14.
A função de autocorrelação (fac) das séries foram representados na Figura 2a1-a4. Observa-se pelo correlograma, que é possível perceber que a série não decai rapidamente para zero, indicando a sua não estacionaridade. Além disso pode-se observar que as autocorrelações tem um decrescimento exponencial lento, sendo outro indício para a presença de tendência nas séries. Segundo Moretin & Toloi (2006), o teste do sinal (Cox-Stuart) pode confirmar a existência ou não dessa componente. Considerando um nível de significância α = 0,05 e tomando-se as 37 observações das séries, todas elas apresentam tendência.
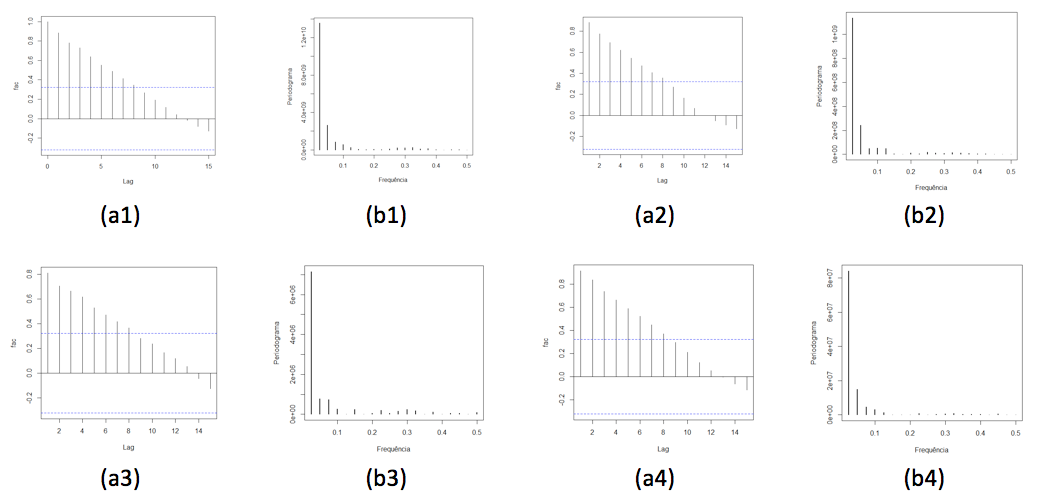
Figura 2. Representação gráfica da função de autocorrelação (a) e o periodograma (b) da produção, área de produção, produtividade e produção de óleo anual de soja no Brasil, das safras de 1977/78 a 2013/14.
O periodograma, Figura 2b1-b4, apresenta a análise espectral, observa-se um pico apenas no primeiro espectro, em todos periodograma com frequência de 0,025, desta forma tem-se um ciclo completo após 40 anos, como foi observado apenas 37 anos, pode-se afirmar que as séries não possuem componente cíclica.
A tendência caracteriza um estágio não-estacionário e, como o ajuste dos modelos pressupõe estacionaridade, as séries foram diferenciadas duas vezes, para eliminar esta componente (Figura 1b1-b4).
Na Figura 3 observa-se o comportamento das funções de autocorrelação e autocorrelação parcial da série diferenciada. Segundo Morettin & Toloi (2006) a facp pode indicar a ordem da parte auto-regressiva e a fac a ordem da parte de médias móveis. Para a produção de soja tem-se que na facp, observa-se os lags 1, 2, 3 e 4 significativos já para fac tem o lag 1 significativo (Figura 3 a1 e b1). A partir disso, os modelos de Box e Jenkins que apresentaram significância de todos parâmetros foram ARIMA (1,2,1), ARIMA (2,2,1). Para a característica área na facp, observa-se os lags 2 e 3 significativos e na fac o lag 2 (Figura 3 a2 e b2), sendo os modelos ARIMA (1,2,1), ARIMA (0,2,2) e ARIMA(2,2,1). Para produtividade na facp, observa-se os lags 1, 2, 3 e 4 significativos e na fac o lag 1 (Figura 3 a3 e b3), sendo os modelos ARIMA (1,2,1), ARIMA (1,2,0) e ARIMA(0,2,1). E para produção de óleo na facp, observa-se os lags 1, 3, 6 e 8 significativos e na fac os lags 1, 9 e 10 (Figura 3 a4 e b4), sendo os modelos ARIMA (1,2,2), ARIMA (8,2,0) e ARIMA(8,2,1). Em cada uma das variáveis foi escolhido o melhor modelo ARIMA para comparar com os modelos linear, quadrático e AEH, os critérios utilizados foram AIC, EQMP e MAPE.
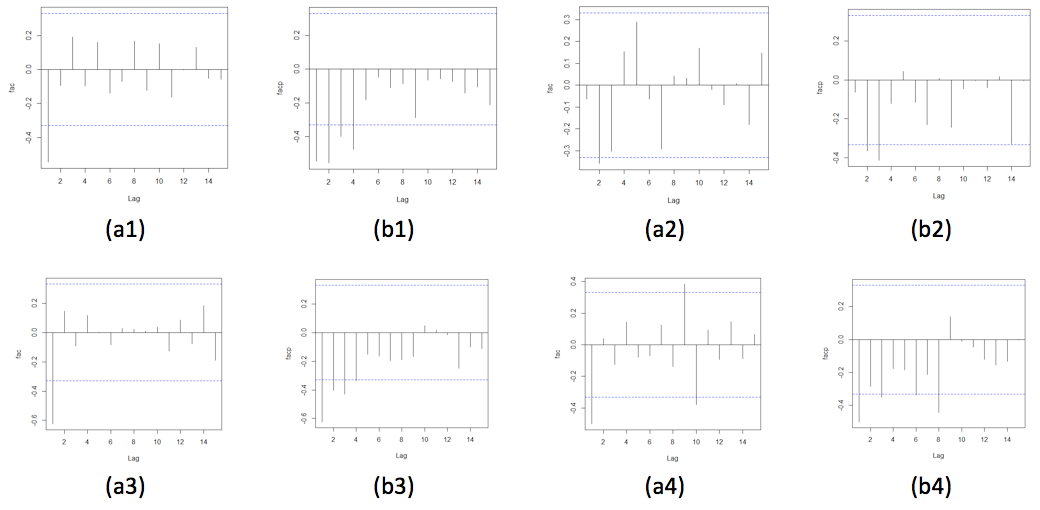
Figura 3. Representação gráfica da função de autocorrelação (fac) (a)
e autocorrelação parcial (facp) (b) da série com segunda diferença
da produção, área de produção, produtividade e produção de óleo anual
de soja no Brasil, das safras de 1977/78 a 2013/14.
Como mencionado, além dos modelos de Box e Jenkins mencionados foram utilizadas outras técnicas de alisamento e de modelagem como o Alisamento Exponencial de Holt (AEH) e modelos lineares polinomiais.
Observe que o modelo linear, apesar de ser o mais utilizado em modelagem de dados com tendência, muitas vezes é usado de forma errada, como na modelagem da tendência para as características produção de soja, área de produção e produção de óleo de soja. O ajuste linear para todas as características em estudo teve o parâmetro angular significativo e altos coeficientes de determinação, 96,85%, 85,7%, 87,1% e 93,7%, para produção, área, produtividade e óleo, respectivamente, mostrando que o modelo linear explica bem a variação total dos dados. Os testes de normalidade nos resíduos por Shapiro-Wilk foram não significativos, com valor-p iguais a 0,4564, 0,2298, 0,1533 e 0,3154, respectivamente, o que se conclui que os resíduos seguem uma distribuição Normal, o teste de Durbin-Watson para independência dos resíduos foram significativo para produção, área e óleo (P<0,001) e não significativo para produtividade, desta forma havendo independência dos resíduos apenas para esta última característica, ainda pode-se observar pela Figura 4-a1, a2 e a4, gráfico dos resíduos, há uma relação quadrática entre as variáveis. Assim, utilizar tal modelo, mesmo que tenha um ótimo coeficiente de determinação para ajustar ou predizer as características de interesse seria um erro muito grande, pois, neste caso a estimativa dos parâmetros são viesadas, os testes de significância não são confiáveis e consequentemente as predições acumulam muitos erros, mas a sua utilização é comum por profissionais de várias áreas. O ajuste quadrático para produtividade não foi significativo, ou seja, não foi rejeitada a hipótese nula de que parâmetro é igual a zero, assim para as demais variáveis com modelo quadrático significativo os testes de normalidade dos resíduos foram todos não significativos com valor-p iguais a 0,2508, 0,4060 e 0,8256, respectivamente, produção, área e óleo. Já o teste de independência dos resíduos foi significativo para área e óleo (P<0,001), mas não significativo para produção, assim o modelo quadrático é um modelo a se considerar na comparação de modelos da variável produção de soja e descartado para as demais características, tem-se ainda pela Figura 4-b2 e b4, que apesar de melhorar o ajuste dos modelos aos dados ainda não se tem uma distribuição aleatória em torno do zero.
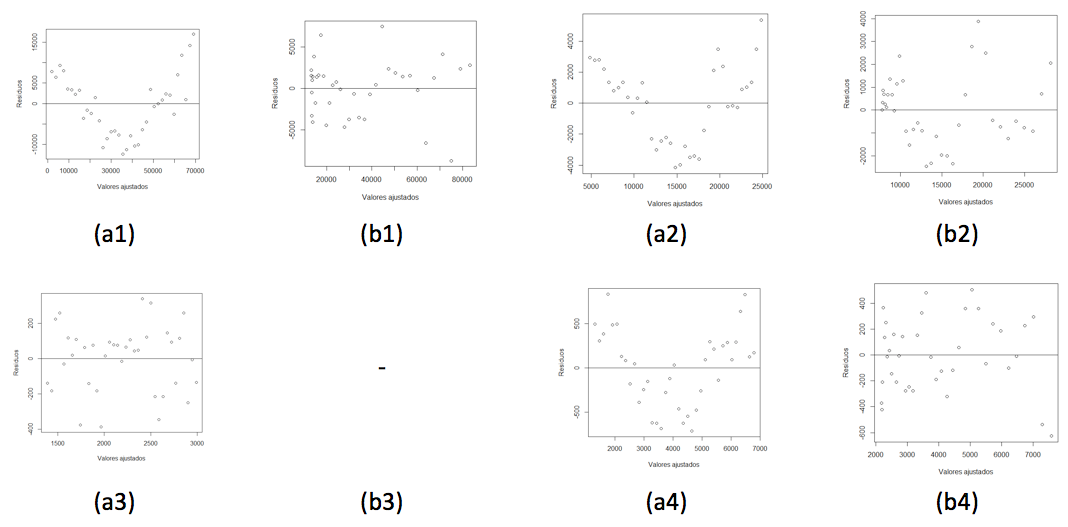
Figura 4. Representação gráfica dos resíduos vs ajustados para os modelos lineares (a) e quadrático (b) da produção, área de produção, produtividade e produção de óleo anual de soja no Brasil, das safras de 1977/78 a 2013/14. ‘-’: modelo quadrático não significativo.
O teste de Box-Pierce foi usado para identificar se o modelo é ruído branco (independente e identicamente distribuído). Para os modelos ARIMA (2,2,1) para produção, ARIMA (2,2,1) para área, ARIMA (1,2,1) para produtividade e ARIMA (8,2,1) para produção de óleo, respectivamente, estatística Q(15)= 5,8586, 8,5277, 10,937 e 4,2315 e valor-p igual a 0,9699, 0,7427, 0,6161 e 0,6454, assim, se observa que os todos modelos ARIMA avaliados constituem ruído.
O estudo do diagnóstico dos resíduos dos modelos de Box & Jenkins (1994) avaliados para as características produção, área, produtividade e produção de óleo permitiu observar que as pressuposições de normalidade foram satisfeitas, como poder ser visto pelo teste de Shapiro-Wilk para a normalidade dos modelos ARIMA (2,2,1) para produção, ARIMA (2,2,1) para área, ARIMA (1,2,1) para produtividade e ARIMA (8,2,1) para produção de óleo, respectivamente, estatística W = 0,9795, 0,9746, 0,9593 e 0,9827 e valor-p igual a 0,7440, 0,5823, 0,2176 e 0,8439.
Tabela 1.
Estimativas dos critérios de AIC, EQMP e MAPE para os modelos univariados avaliados.
Característica |
Modelo |
AIC |
EQMP |
MAPE |
Produção de soja |
ARIMA (2,2,1) |
689,37 |
15.622.528 |
10,71% |
AEH |
- |
17.686.419 |
10,70% |
|
Linear |
767,71 |
53.921.621 |
24,81% |
|
Quadrático |
713,38 |
11.143.614 |
10,16% |
|
Área de produção |
ARIMA (2,2,1) |
592,6 |
978.660,5 |
5,19% |
AEH |
- |
1.409.521,0 |
6,57% |
|
Linear |
687,6 |
5.858.189,0 |
15,94% |
|
Quadrático |
651,8 |
2.229.764,0 |
8,60% |
|
Produtividade |
ARIMA (1,2,1) |
489,8 |
49.260,5 |
8,02% |
AEH |
- |
49.144,3 |
8,53% |
|
Linear |
469,5 |
33.503,5 |
7,37% |
|
Produção de Óleo |
ARIMA (8,2,1) |
502,5 |
43.238,41 |
4,34% |
AEH |
- |
90.966,19 |
6,94% |
|
Linear |
558,0 |
176.483,50 |
10,68% |
|
Quadrático |
527,6 |
77.576,09 |
6,56% |
Nota: ‘-’: não se aplica.
Os modelos univariados com menores AIC, EQMP e MAPE (Tabela 1) para as características produção, área, produtividade e produção de óleo foram, respectivamente, os modelos: quadrático, ARIMA (2,2,1), linear e ARIMA (8,2,1) (Tabela 1). Sendo então os modelos escolhidos para estimar as previsões de tais variáveis (Figura 5). Os modelos linear e quadrático são apresentados na Figura 5.
Recentemente houve o fechamento da safra 2014/15, que segundo informativo da Celeres® (2015) a produção de soja foi de 95,6 (milhão de tonelada), 11% maior que safra 2013/14, já a área teve um aumento de 4,5% em relação à safra anterior, com 31,46 (milhão de hectare). Apesar o menor nível de investimento em comparação à safra 2013/14 e também da irregularidade climática, a produtividade foi de 3,04 (t/ha), um crescimento de 6,1% quando comparada com a safra anterior e a produção de óleo de 7,6 (milhão de tonelada) um aumento de 8,6%.
No comparativo dos resultados previstos pelos modelos univariados para estas características da cultura da soja com este recém fechamento de safra, tem-se que a produção de soja prevista foi inferior ao real, com 87,6 (milhão de tonelada) (Tabela 2), um erro de aproximadamente 8 (milhão de tonelada), este erro está abaixo de 8,5% da produção anual, ou ainda, equivale a produção da região Nordeste (Maranhão, Piauí e Bahia), que hoje representa 8,6% da produção brasileira. A área plantada também prevista também foi inferior ao real, com 31,3 (milhão de hectare) (Tabela 2), mas o erro foi menor de 0,2 (milhão de hectare), equivalente a 0,6% de toda área plantada, ou seja, seis vezes menor que a área plantada em toda Norte do país, sendo que esta região representa menos de 4% de toda área de plantação de soja do Brasil. Apesar de ser o modelo mais simples, linear, a estimativa prevista para a safra de 2014/15 da produtividade obteve o menor erro de previsão 0,005(t/ha), sendo o valor previsto aproximadamente igual ao real em 3,035 (t/ha) e para a produção de óleo de soja uma previsão de 7,22 (milhão de tonelada) para safra 2014/15, um erro de 0,4 (milhão de tonelada), ou seja, 5% da produção de óleo total. De forma geral os modelos tiveram bons desempenhos em estimar previsões um ponto à frente, visto que os erros foram inferiores a 8,5% do valor verdadeiro (Figura 5).
Tabela 2.
Valores previstos dos modelos univariados adotados para produção, área,
produtividade e produção de óleo de soja anual, das safras de 2014/15 a 2018/19,
inclusive intervalos de confiança.
Modelo |
Ano |
Zt(h) |
LI |
LS |
Quadrático (Produção, mil toneladas) |
2015 |
87584,99 |
79792,89 |
95377,08 |
2016 |
92003,39 |
84206,29 |
99800,49 |
|
2017 |
96549,35 |
88746,96 |
104351,74 |
|
2018 |
101222,87 |
93414,89 |
109030,85 |
|
2019 |
106023,95 |
98210,10 |
113837,80 |
|
ARIMA (2,2,1) (Área, mil toneladas) |
2015 |
31281,60 |
29288,00 |
33275,19 |
2016 |
31828,58 |
28040,19 |
35616,97 |
|
2017 |
32606,83 |
27580,80 |
37632,86 |
|
2018 |
33715,69 |
27805,88 |
39625,51 |
|
2019 |
34900,02 |
28170,78 |
41629,26 |
|
Linear (Produtividade, kg/ha) |
2015 |
3034,65 |
2631,65 |
3437,65 |
2016 |
3079,11 |
2674,44 |
3483,78 |
|
2017 |
3123,58 |
2717,16 |
3529,99 |
|
2018 |
3168,05 |
2759,80 |
3576,29 |
|
2019 |
3212,51 |
2802,37 |
3622,66 |
|
ARIMA (8,2,1) (Óleo, mil toneladas) |
2015 |
7224,13 |
6805,10 |
7643,17 |
2016 |
7638,34 |
7010,58 |
8266,10 |
|
2017 |
7627,49 |
6890,35 |
8364,63 |
|
2018 |
7831,39 |
6992,83 |
8669,96 |
|
2019 |
8236,24 |
7283,48 |
9189,00 |
Nota: Zt(h): valor predito; LI: limite inferior de predição; LS: limite superior de predição.
Assim, este aumento na produção de soja brasileira foi interessante tanto no cenário nacional como internacional, pois a soja obteve altas cotações na bolsa de Chicago (em média US$ 10,00/bushel), reflexo da piora das condições de lavoura nos Estados Unidos, em que segundo USDA (2015) houve um atraso de 5% da área total semeada, causada pelo acúmulo de chuva nas áreas produtoras, o que pode prejudicar o desenvolvimento da planta, perdas no período de colheita com o agravante da possibilidade de neve. No Brasil no dia 10/08/15 a cotação em Paranaguá estava de R$ 79,29/sc um aumento de 18,1% comparado ao mesmo período do ano anterior. Foram embarcadas em junho/15, 9,81 milhões de toneladas do grão, valor alto para um único mês e 42% maior que no mesmo mês de 2014. Com as vendas recordes do último mês, o acumulado semestral ficou em 32,2 milhões de toneladas (1,5% acima que o ano passado) (Brasil, 2015).
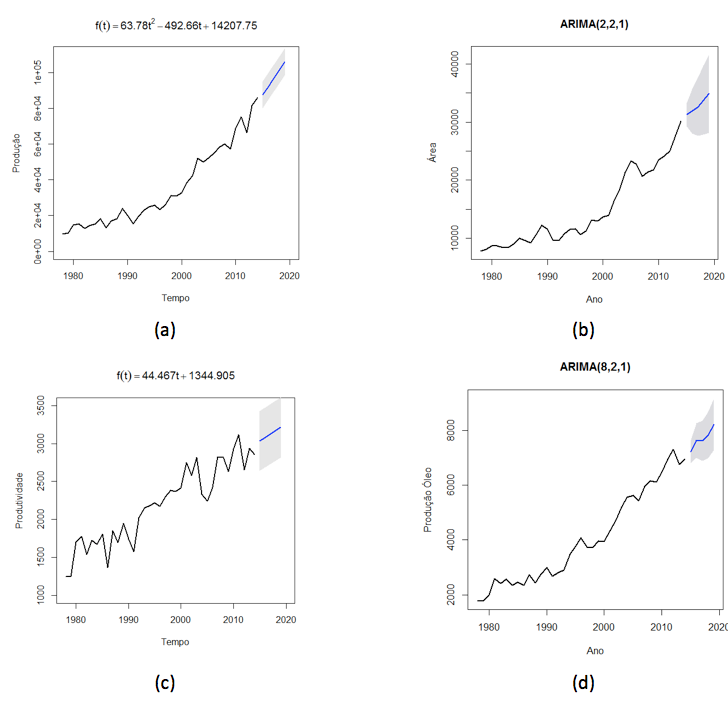
Figura 5. Representação gráfica dos melhores modelos avaliados com os
valores observados e respectivas previsões da produção (a), área de produção
(b), produtividade (c) e produção de óleo (d) anual de soja no Brasil,
das safras de 1977/78 a 2013/14, inclusive o intervalo de previsão.
Para o caso multivariado foi calculado inicialmente as correlações entre as variáveis em estudo, sendo que tomadas duas a duas a menor correlação foi para área e produtividade de 0,8253, mostrando então um grau de relação entre elas forte e positivo.
A escolha da ordem auto-regressivo para o estudo multivariado a partir da metodologia de vetores auto-regressivos (VAR(p)) foi feita baseado nas medidas das estatísticas de AIC e BIC, sendo que seus menores valores foram para defasagens iguais a cinco, assim o valor da ordem foi p=5, desta forma o modelo estudado foi o VAR(5). Este modelo resultou na significância ou na dependência de valores passados para cada série de característica da cultura da soja estudada. Assim, tem-se os modelos para cada variável:
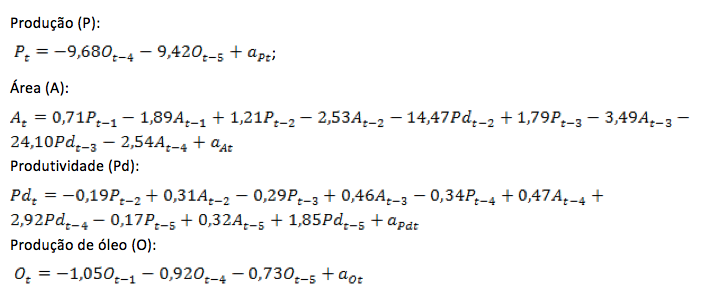
Assim, a produção é influenciada por valores passados da produção de óleo, a área por valores da própria área e produção e produtividade, o mesmo para produtividade, já para produção de óleo apenas pelos valores passados da produção de óleo.
A verificação das pressuposições do modelo multivariado foi realizada, semelhantemente aos univariados, sendo o teste multivariado de Portmanteau para verificar se o modelo tem ruído branco, o valor-p foi 0,126, assim o teste foi não significativo, não rejeitando a hipótese nula de ruído branco. Pelo teste de normalidade multivariado Jarque-Bera o valor-p foi de 0,912, assim existe a normalidade.
As previsões a partir nos modelos multivariados não se mostraram mais interessantes que as dos modelos univariados (Tabela 3) devido aos altos valores dos MAPE’s, quando comparados aos univariados. Apesar que a estimativa real da safra 2014/15 para produção ter ficado fora do intervalo de confiança de previsão no caso univariado, mas ficou bem próximo ao limite superior, e não ter ocorrido o mesmo para o modelo multivariado, onde o valor real ficou dentro do intervalo. Este fato foi o ponto positivo da modelagem multivariada, mas as outras estimativas, quando comparada com a real desta mesma safra, tiveram um erro bem maior, o que acabou por acarretar MAPE’s maiores.
Tabela 3. Valores previstos pelo modelo multivariado auto-regressivo VAR(5)
para produção, área, produtividade e produção de óleo de soja anual,
das safras de 2014/15 a 2018/19, inclusive intervalos de confiança.
Variável |
Ano |
Zt(h) |
LI |
LS |
MAPE |
Produção |
2015 |
90635,49 |
83954.60 |
97316.37 |
14,25% |
2016 |
97419,39 |
89790.24 |
105048.54 |
||
2017 |
95621,99 |
86795.19 |
104448.80 |
||
2018 |
116053,91 |
106501.35 |
125606.47 |
||
2019 |
114804,29 |
104316.10 |
125292.48 |
||
Área |
2015 |
29986.09 |
28145.47 |
31826.71 |
18,87% |
2016 |
33203.54 |
30522.42 |
35884.65 |
||
2017 |
36380.21 |
33214.09 |
39546.32 |
||
2018 |
38576.11 |
35077.60 |
42074.62 |
||
2019 |
40169.32 |
36259.85 |
44078.78 |
||
Produtividade |
2015 |
3081.017 |
2779.194 |
3382.839 |
12,07% |
2016 |
2858.250 |
2502.934 |
3213.565 |
||
2017 |
2431.867 |
1909.297 |
2954.436 |
||
2018 |
3054.673 |
2524.755 |
3584.591 |
||
2019 |
2582.690 |
2039.400 |
3125.980 |
||
Óleo |
2015 |
8174.705 |
7803.343 |
8546.066 |
30,07% |
2016 |
7803.679 |
7359.819 |
8247.538 |
||
2017 |
8084.045 |
7520.210 |
8647.881 |
||
2018 |
8709.259 |
8026.395 |
9392.124 |
||
2019 |
8946.321 |
8218.592 |
9674.050 |
As séries apresentaram apenas a componente de tendência, não havendo a componente cíclica.
Com exceção aos modelos de tendência linear e/ou quadrática, todos modelos propostos e avaliados se adequaram à série em estudo, visto pelo diagnóstico dos resíduos as pressuposições satisfeitas. Os modelos lineares não se ajustaram bem devido a dependência residual e também por não haver uma relação linear entre as variáveis e tempo, exceto para produtividade. No caso dos modelos quadráticos se ajustou bem apenas para produção.
Foi previsto pelo modelo quadrático para a safra 2014/15 uma produção anual de 87,6 milhões de toneladas de soja no Brasil, representa um aumento de aproximadamente 2% sobre a safra anterior, podendo atingir, pelo intervalo de previsão, um aumento máximo de 11% (95,4 milhões de toneladas), sendo a China, um dos maiores importadores mundiais do grão.
Foi previsto pelo modelo ARIMA (2,2,1) para a safra 2014/15 uma área anual de 31,3 milhões de hectares de soja no Brasil, representa um aumento de aproximadamente 4% sobre a safra anterior, podendo atingir, pelo intervalo de previsão, um aumento máximo de 10% (33,3 milhões de hectares).
Foi previsto pelo modelo linear para a safra 2014/15 uma produtividade anual de 3034,6 kg/hectares de soja no Brasil, representa um aumento de aproximadamente 6% sobre a safra anterior, podendo atingir, pelo intervalo de previsão, um aumento máximo de 20% (3437,6 kg/hectares).
Foi previsto pelo modelo ARIMA (8,2,1) para a safra 2014/15 uma produção anual de 7.224,13 milhões de toneladas de óleo de soja no Brasil, representa um aumento de aproximadamente 4% sobre a safra anterior, podendo atingir, pelo intervalo de predição, um aumento máximo de 10% (7.643,17 milhões de toneladas).
Com o objetivo de previsão os modelos univariados foram mais eficientes que o multivariado, como mostra o resultado do MAPE, mas pelo multivariado observou-se a relação entre as variáveis, que se mostrou interessante.
Agradecemos a CAPES e a FAPEMIG pelo apoio para desenvolver esse trabalho.
BRASIL (2009). Relatório de Gestão: Ministério da Agricultura, Pecuária e Abastecimento (MAPA). Disponível em: http://www.agricultura.gov.br/arq_editor/image/RELATORIO_GESTAO/GM/2004.pdf
BRASIL (2015). Estatísticas do Comércio Exterior do Ministério do Desenvolvimento, Industrial e Comércio Exterior (MDIC). Disponível em: http://www.mdic.gov.br//sitio/interna/interna.php?area=5&menu=5074&refr=1161
Box, G. E. P.; Jenkins, G. M.; Reinsel, G. C. (1994). Time Series Analysis: forecasting and control. New Jersey: Prentice Hall.
Contini, E.; Gasques, J. G.; Leonardi, R. B. A. de; Bastos, E. T (janeiro, 2006). Evolução e tendências do agronegócio. Revista de Política Agrícola, 1, 5-28.
Morettin, P. A.; Toloi, C. (2006). Análise de séries temporais. Blucher.
Osaki, M.; Batalha, M. O (2011). Produção de biodiesel e óleo vegetal no Brasil: realidade e desafio. Organizações Rurais & Agroindustriais, 13 (2), 227-242.
Priestley, M. B. (1989). Spectral analysis and time series. New York: Academic Press.
R Development Core Team (2015). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Disponível em: http://www.R-project.org/
Seibel, F (2015). O novo salto do agronegócio. Exame. Disponível em: http://exame.abril.com.br/revista-exame/edicoes/895/noticias/o-novo-salto-do-agronegocio-m0131023
USDA (2015). Foreign Agricultural Service (FAS). Disponível em http://apps.fas.usda.gov/psdonline/psdQuery.aspx
Vilarinho, M. R (2015). Questões sanitárias e o agronegócio brasileiro. Disponível em http://www.embrapa.br/embrapa/
Winters, P. R. (1960). Forescasting sales by exponentially weighted moving average. Management Science, 6, 324-342.
1. Universidade Federal de Uberlândia. Doutor em Agronomia. E-mail: quintiliano.nomelini@ufu.br
2. Universidade Federal de Alfenas. Doutor em Estatística e Experimentação Agropecuária. E-mail: eric.ferreira@unifal-mg.edu.br
3. Universidade Federal de Alfenas. Doutor em Estatística e Experimentação Agropecuária. E-mail: denismar.nogueira@unifal-mg.edu.br
4. Instituto Federal de Goiás Campus Morrinhos. Doutor em Ciências Veterinárias. E-mail: anselmo.golynski@ifgoiano.edu.br
5. Instituto Federal de Goiás Campus Morrinhos. Doutor em Produção Vegetal. E-mail: adelmo.golynski@ifgoiano.edu.br
6. Universidade Federal de Uberlândia. Graduando em Estatística. E-mail: thacyo@est.ufu.br