 HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN
HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN Espacios. Vol. 37 (Nº 22) Año 2016. Pág. 5
José DONIZETTI de Lima 1; Gilson ADAMCZUK Oliveira 2;Marcelo Gonçalves TRENTIN 3; Dayse Regina BATISTUS 4; Cassiane Bayerl POZZA 5
Recibido: 25/03/16 • Aprobado: 13/04/2016
Appendix I - Complementary results
ABSTRACT: A systematic approach for evaluating the performance of individual techniques and their combinations to forecast urban water demand is proposed and organized into four phases in this work. It uses three forecasting techniques: exponential smoothing (ES), seasonal autoregressive integrated moving average (SARIMA) and artificial neural networks (ANN) models. 14 combinations of forecasts are evaluated with the goal of improving the estimation accuracy. This systematic approach was applied to monthly data over an interval from 2000 until 2011 (with a validation set of 12 months). Data from 10 cities in the state of Paraná, Brazil were evaluated. In choosing the best model for each city, the combinations are highlighted. According to a Mean Absolute Percentage Error (MAPE) criterion, results indicate that the choice of the most accurate model of ES or SARIMA produces the best forecasting global performance, which had the smallest standard deviation (0.667%) and a MAPE of 3.297%. |
RESUMEN: Este trabajo presenta un enfoque sistemático para evaluar el rendimiento de las técnicas individuales y sus combinaciones para la previsión de demanda de agua urbana. Este trabajose organiza en cuatro fases. Utiliza tres técnicas de predicción: alisado exponencial (ES), estacional autorregresiva integrada de media móvil (SARIMA) y modelos de redes neuronales artificiales (ANN). 14 combinaciones de pronósticos se evalúan con el objetivo de mejorar la precisión de la estimación. Este enfoque sistemático se aplicó a los datos mensuales sobre un intervalo desde 2000 hasta 2011 (con un sistema de validación de 12 meses). Se evaluaron datos de 10 ciudades en el estado de Paraná, Brasil. Se destacan las combinaciones para elegir el mejor modelo para cada ciudad. Según un criterio de Error de porcentaje absoluto medio (MAPE), los resultados indican que la elección del modelo más preciso de CE o SARIMA ya que produce el mejor pronóstico de rendimiento global, porque presenta la desviación estándar más pequeña (0.667%) y un mapa de 3.297%. Palabras clave:demanda de agua urbana, proyecciones técnicas, series temporales, redes neuronales, predicción de combinación. |
Nowadays, approximately 36% of the world population or around 2.4 billion people live in water-scarce regions and 22% of the global gross domestic product (GDP) is produced in areas with problems related to water shortage, stress, or crisis. According to the analysis of the International Food Policy Research Institute (IFPR), if the current water management practice and consumption tendencies are maintained, 45% of the predicted GDP for 2050 will be at risk. This would be equivalent to 1.5 times the size of the current global economy. In addition, approximately 4.8 billion people (or 52% of the entire world population) will be exposed to serious water shortages by 2050 (VWNA, 2012).
The search for a sustainable water consumption policy is a way to avoid those pessimistic projections, or at least to lessen their impact in the world. The challenge of this remains in the alliance between the growth of the population and economy and the rational use of water resources. Operations research will play a major role in this task, and the authors regard the use of time series adjustment for monthly water demand in this context.
In comparison with the world's state of affairs, Brazil is in a comfortable situation regarding its water resources. The availability of water indicates an adequate situation when compared with the values from other countries listed by the United Nations (UN). However, in spite of this apparently comfortable situation, the spatial distribution of water resources in Brazil is unequal. More than 80% of the water resources are concentrated in the Amazon basin region, which has the lowest human population density in the country, along with a reduced demand for urban, industrial, and irrigation use. (ANA, 2012).
The water withdrawal volume corresponds to the amount of water obtained by water companies from rivers, large natural reservoirs, water storage dams, or other sources of water to be explored. Water withdrawal is performed by means of pumping, and the streamline is directed to the water treatment stations where chemical products are added to process the water.
Water companies need an adequate forecasting system to allow one to develop short-term, medium-term, and long-term planning. With this in mind, the manager can plan the company's premises, and allow the water-supplied community to adopt actions and develop its own plans to implement a sustainable use of this resource.
The goal of this paper is to propose a systematic approach for evaluating the performance of individual techniques and their combinations to forecast the withdrawal of water volume by water companies. Even considering that there are losses in the distribution of water, this volume represents the water demand in urban centers. In this work, the time horizon used in the study was 12 months. Section 2 provides a review of the forecasting techniques applied to the water demand (2.1) and the growing tendency that is represented by the combination of forecasting techniques (2.2), although this is only used in urban water demand forecasting occasionally. The combination of techniques aims at decreasing the residual variance and improving the forecasting accuracy (2.3). In section 3, a detailed systematic approach is proposed, being the original main contribution of this work. Another contribution of this paper is the wide range of combinations that are tested and evaluated comparatively, something unusual in time series literature (Martins & Werner, 2012). In section 4, the systematic approach is applied with a good level of details using a data set of 10 years from 10 cities of the southwestern region of the state of Paraná, Brazil. Section 4 also provides a discussion of the results. Conclusions and considerations are presented in section 5.
A time series is a set of observations obtained in a sequential and systematic way over an interval of time. Among the time series, techniques presented in the literature to analyze a set of values obtained during a time interval, two classes of models play an important role: the exponential smoothing models (ES) and the autoregressive integrated moving average (ARIMA) models (Makridakis et al., 1998; Armstrong, 2001; Morettin & Toloi, 2006). On the other hand, the artificial neural networks used in the computational intelligence approach for time series have shown promising results (Calôba et al., 2002; Dias, 2006; Martins & Werner, 2012; Wu et al., 2013).
Regarding the techniques of artificial intelligence, Wu et al. (2013) recommend artificial neural networks (ANN) with a radial basis function due to their potential to approximate nonlinear behavior. According to these authors, the performance of ANN is influenced by the calibration of its parameters. Among these are: (i) the number of occurrence in the input vector (n), which characterizes the unit delays along the time series; (ii) the eg value, which is used to give an objective to the neural network; the network's training uses Root Mean Squared Error (RMSE) as a calibration parameter; and (iii) the width of the receptive fields (sc), which interferes with the outputs of the units contained in the hidden layer of the network.
According to Martins and Werner (2012), the use of a Box-Jenkins methodology (ARIMA) is reasonable since this class is formed by robust models which are consolidated and have a wide range of applications. Moreover, the class of ES models is important because of its simplicity, ease of computational implementation, and for the associated history of promising results, as in the study entitled "M-Competition" (Makridakis & Hibon, 2000; Nikolopoulos et al., 2011a).
The forecasting methods can be understood as the way one or more of such techniques are used. Therefore, a combination of forecasting methods is a part of a forecasting methodology. In the following sections, techniques and methods applied to the specific case of water demand (2.1) and a detailed evaluation of the forecasting combinations (2.2 and 2.3) are given, since they are the core element of the forecasting systematic approach proposed in this work.
Water demand studies have been considering hours, days, weeks, and months as short-term predictions, whereas years are considered long-term predictions. This cannot be understood using the terms used for forecast horizons in time series studies, where "short" and "long" are related to the distance from the origin of forecasts.
Short- and long-term water demand results have been studied over the last 50 years and such studies can be divided into five categories: regression analysis, time-series analysis, computational intelligence approach, hybrid approaches, and Monte-Carlo simulation approach (Qi & Chang, 2011). Among the five categories, only regression analysis gives the same importance to the short- and long-term ranges. The remaining categories have their applications concentrated in the short-term demand. In recent years, such categories have been used for the prediction of urban water demand, and therefore they are listed in Table 1. A growing tendency in the usage of hybrid strategies is also observed, in which at least two techniques or approaches are applied in the elaboration of forecasting methodologies. It is also worth noticing the growing importance of neural networks in the water demand forecasting field, either in an isolated manner or combined with other techniques.
Table 1: Works about urban water demand in the last five years
Literature |
Technique/Method Used |
Accuracy Criteria |
Time unit |
Adamowski (2008) |
Multiple linear regression, ARIMA and artificial neural networks. |
MAPE and R2 |
Days |
Ghiassi et al. (2008) |
Dynamic model of artificial neural network. |
MAPE |
Days, Weeks and Months |
Caiado (2010) |
ES (Holt Winters), ARIMA and GARCH (generalized autoregressive conditional heteroskedasticity). Simple forecasting combination and combination using the reciprocal of the MSE to determine weights. |
MSE |
Days |
Firat et al. (2010) |
Artificial neural networks. |
MAPE, NRMSE and TSx |
Months |
Mohamed & Al-Mualla (2010) |
Constant rate model. Method use two sets of data: one to provide a yearly rate and a second one to include the short-term term. |
MAPE and SAPE |
Years |
Herrera et al. (2010) |
Artificial neural networks, regressive models, model based on a past average value adjusted by the more recent residues (errors). |
RMSE and MAE |
Hours |
Qi & Chang (2011) |
Dynamic model of a system based on two macroeconomic indicators: unemployment rate and average income per annum. Use of regression. |
R2 |
Years |
Almutaz et al. (2012) |
Monte Carlo simulation |
s |
Months |
Azadeh (2012) |
Hybrid approach of artificial neural networks, linear Fuzzy regression and ANOVA. |
MAPE |
Days |
Campisi-Pinto et al. (2012) |
Artificial neural networks combined with wavelet-denoising. |
R, RMSE, FSE, E and B |
Months |
Yasar et al. (2012) |
Stepwise multiple regression. |
R and MAPE |
Months |
Zhai et al. (2012) |
Authors use time series analysis without showing the used models. |
Not mentioned |
Years |
Source: Elaborated by the authors.
Regarding the accuracy criteria used in the validation or model fitting, Table 1 shows that there is a predominant set of criteria that are widely used in time series analysis and computational intelligence approaches. Mean Absolute Percentage Error (MAPE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) appear to be consistently used in recent researches. Other criteria, such as the Standard deviation of the Absolute Percentage Error (SAPE), the Normalized Root Mean Squared Error (NRMSE) and the Fractional Standard Error (FSE) can be considered as extensions or derivations of the previously mentioned criteria. The correlation coefficient (R) and the determination coefficient (R2) are typically used in techniques involving regression, even considering that the R2 can be used in time series models. In the only work that uses Monte Carlos simulation, Almutaz et al. (2012) uses the standard deviation (s) to verify the accuracy of the predictions.
Still regarding the accuracy, the utilization of unusual measurements in time series analysis, such as the TSx, that can be seen in Firat et al. (2010), and E and B criteria used by Campisi-Pinto et al. (2012), can be represented by:
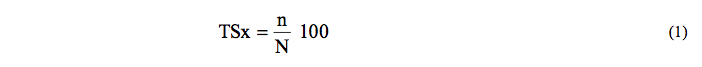
In this equation, TSx is the threshold statistic for a level of x%, where n is the total number of forecasts having a relative forecast error smaller than x%, and N is the total number of forecasts. According to Firat et al. (2010), TSx quantifies the consistency of the forecast errors for a particular model.
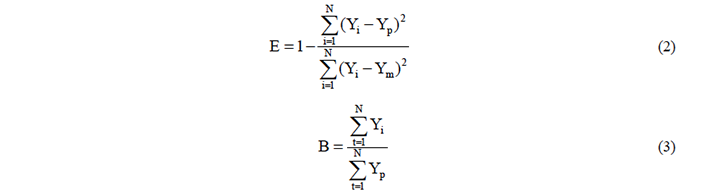
The parameter E is the Nash-Sutcliffe model efficiency, Yi are the real values in period i, Yp are the forecasted values in this period, and Ym represents the average value of the series of data. E is widely used in hydrology because it measures the ability of the model to forecast values which are different from the average. The index B provides a good measure of whether the model is overestimating (B > 1) or underestimating (B < 1) compared to observed values. B = 1 indicates non-biased model performance (Campisi-Pinto et al., 2012).
Finally, it can be seen in Table 1 that the studies on water demand for urban use are more concentrated in short-term forecasts (75%), from hours to a few months. Short-term forecasts are important from the standpoint of the control of the water company premises or equipment. One could even identify losses at a schedule point which shows a demand that is much different from what was expected. On the other side, from the strategic standpoint, the long-term projections (in years) correspond to a relatively low number (25%), and they may relate to the planning of the water companies' expansion or to the study of the possibility of water shortage occurrences in urban centers (domestic/industrial).
There are a considerable number of applications using the combination of forecasting time series techniques (ES, ARIMA and ANN) in other areas (Calôba et al., 2002; Stock & Watson, 2004; Andrawis et al., 2011; Martins & Werner, 2012; Wu et al., 2013). For urban water demand, the adoption of this strategy is still incipient and constitutes an approach to be explored, especially if used for long-term forecasts (years). Qi & Chang (2011) have commented that such univariate models have low reliability to represent all the involved factors that affect the consumption of water. As a consequence, its use is concentrated in the short-term forecasts.
Bates and Granger (1969) introduced the combination of forecasts when they were stimulated by the search for a technique that presented the lowest possible error. This method incorporates forecasts obtained from different techniques, with the goal of improving the accuracy of the forecasts while extracting useful and independent information from the available data (Panagiotopoulos, 2011).
The utilization of forecast combinations is justified by the facts that: (i) there is no perfect forecasting technique, since there is no way to acquire the reality exactly as it is; (ii) it's not known if a forecasting technique will always present a better performance than other techniques in all periods and forecast horizon intervals using the whole series of data (Flores & White, 1988); (iii) the accuracy of an individual forecasting technique is sensitive to several factors (Makridakis et al., 1998); (iv) the choice of an individual forecasting technique from a set of available techniques is riskier than choosing a combination of them (Hibon & Evgeniou, 2005); and (v) the combination of forecasts can present forecasts which are more robust than those obtained by individual techniques (Souza, 2008).
Several studies have contributed to reinforce that forecast combinations can bring significant benefits in terms of forecast accuracy (Clemen, 1989; Makridakis et al., 1998; Andrawis et al., 2011). However, although there may be a concentration of efforts to verify which forms of combinations would be the most cohesive for the improvement of forecasts, there are no unanimous results (Martins & Werner, 2012).
According to Flores and White (1988), in order to use a combination of forecasts, the selection of the base forecast techniques is necessary to determine which forecasts to include in the combination. One must then choose the combination methods, which is how the individual techniques will be combined. For Werner and Ribeiro (2006), the choice of the individual techniques depends on five factors, namely: accuracy, forecast horizon, costs, complexity, and availability of data. This confirms the difficulty of executing such a task.
However, combined forecasts have been useful when it is difficult to select the most accurate forecasting method (Panagiotopoulos, 2011). In addition, combination methods that are considered more complex not always demonstrate a superior performance in comparison with simpler methods when the forecast accuracy is concerned (Stock & Watson, 2004; Konig et al., 2005).
For the choice of the best forecast, the analysis of a variety of techniques (including combinations) and the verification of which one provides the best accuracy value is necessary. For this purpose, one can use relative or absolute measures like MAPE, MSE or MAE. The incorporation of more than one comparison criteria is recommended, because different criteria may provide different indications of performance (Werner, 2012).
Joint analysis and absence of concurrence among the forecasting techniques are supported in the literature, since the proposed use of a final model that adds the forecasting power of more than one technique is being successfully utilized in different areas of research (Clemen, 1989; Makridakis et al., 1998; Andrawis et al., 2011). In the following section, proposed configurations for the forecasting combinations are presented.
The combination of forecasts can be represented by:
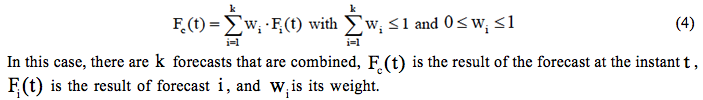
The main methods that estimate weights in forecast combinations are presented in the following paragraphs.
The simplest way to combine individual forecasts is to attribute the same weight to all of them. In this case, one has the arithmetic mean expressed by:
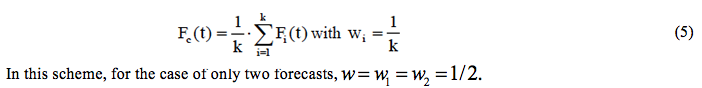
According to Werner (2012), the use of a forecast combination with arithmetic mean is a frequent practice because it is one of the most known procedures and is also easy to implement in a computer. This type of average, even considering that it does not use optimal weights, can generate better results than more sophisticated methods. Other similar forms of combination are the geometric mean (Faria & Mubwandarikwa, 2008), exposed in equation 6, and the harmonic mean (equation 7).
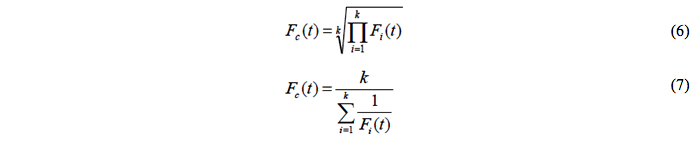
The approach in which the weights are values that are inversely proportional to a certain accuracy measure was the most sophisticated method presented by Bates and Granger (1969). For such a purpose, forecasts are combined in agreement with their individual performances. More specifically, the weight of a forecast is established in agreement with the accuracy of a forecast that was compared to the sum of all the forecasting methods. For Newbold and Bos (1994), methods that have a better performance must have a larger weight. In this context, weights are assumed to be inversely proportional to the accuracy indexes of all the techniques. The formulas that calculate the weights based on values that are inversely proportional to MAPE (equation 8), MSE (equation 9), and MAE (equation 10), are:
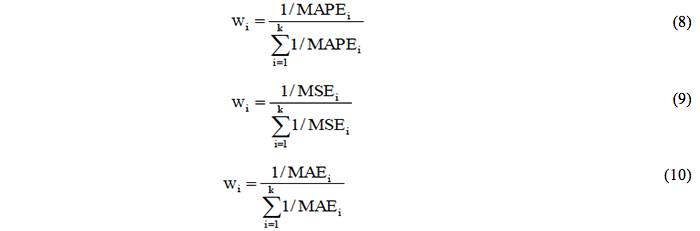
In which the parameters are as previously defined.
In the approach using the minimum variance method, the weights are calculated in a way that the errors variance of the combined forecasts may be minimized. In this case, the two forecasts are assumed to be unbiased, with variances in the forecasting errors equal to and , respectively (Werner & Ribeiro, 2006; Andrawis et al., 2011; Martins & Werner, 2012). Assuming as the covariance of the forecasting errors from the two techniques and assuming that the weights add up to 1, it is demonstrated that the optimal weights are:
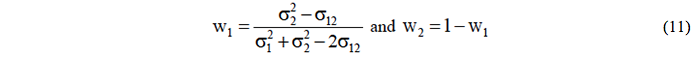
According to Andrawis et al. (2011) the error in the covariance estimation can have an impact on the combined forecasting accuracy. In this context, if the covariance between the two forecasting techniques is not considered, the optimal weights are determined by:
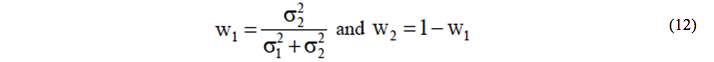
Stock and Watson (1999) introduced a method in which the weights are calculated using a function that is inversely proportional to the mean square error (MSE). This approach is very similar to the uncorrelated minimum variance method presented in equation (9).
When there are two forecasts to be combined, an alternative approach to calculate the weights for the forecast is to use a multiple linear regression model. According to Granger and Ramanathan (1984), the conventional methods that combine forecasts can be viewed as a structured form of regression. These authors state that the methods are equivalent to the ordinary least squares method (OLS), where the combined forecast is the response variable and the individual forecasts are the explanatory variables.
In accordance with Andrawis et al. (2011) there are typically three equations that change according to the flexibility that is allowed in the weights, being given by:
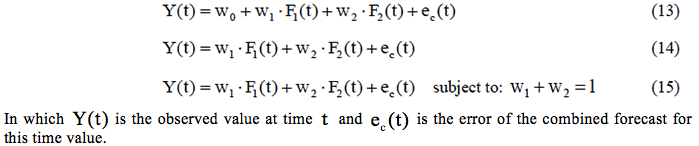
The model expressed by equation (13) contains an intercept that can be useful to correct any possibility of biasing. Secondly, in the models presented in equations (14) and (15) it is assumed that the individual models are not biased.
In the method that uses weights based on absolute errors, weights are designated in accordance with the number of times that the corresponding technique is better than the others, and it is executed by means of a relative frequency (Panagiotopoulos, 2011). One way to use this approach for two techniques is to use a logical function, like:
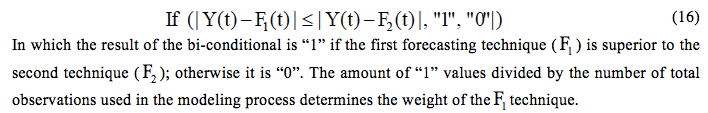
The determination of weights in combinations can be also obtained by using linear programming (LP). Relevant studies dealing with this theme are detailed in Panagiotopoulos (2011). The mathematical elaboration of weight estimation to minimize MAPE, MSE and MAE, restricted to weights in a "0" to "1" interval, can be represented by:
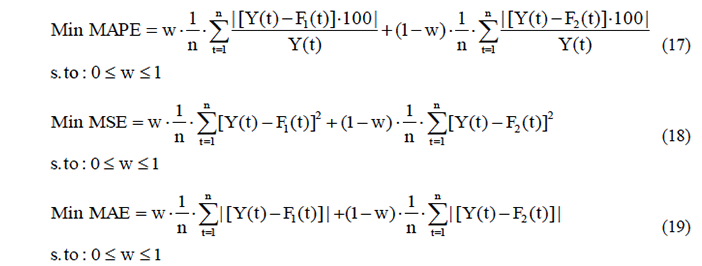
In equations (17), (18), and (19), the number of observations in the procedure is given by .
There are many methods available in the literature to determine the weights used in the combination of individual forecasting techniques. However, the 14 methods presented in equations (5) to (19) have been elected as the most adequate in the scope of this study. Based on the above considerations, the next section presents the methodology proposed for this research.
Because there is no unanimous agreement among authors about which individual techniques or methods of combination provide more accurate forecasts, in this study three individual techniques (ES, SARIMA, and ANN) and fourteen combination methods are tested, both with objective approaches. By doing this, the reduction of risks and confidence intervals are established as goals, as well as the use of independent information from different methods.
Major problems, given their magnitude and complexity, must be broken down into phases and stages. This is the case during the implementation of a forecasting system for the volume of withdrawn water in cities aiming at the public supply. In this context, this study used the propositions by Makridakis et al. (1998) as a basis, recommending the following steps: (i) problem definition; (ii) information gathering; (iii) preliminary analysis of data; (iv) model choice and fitting; and (v) use and evaluation of the forecasting model. Recommendations elaborated by Armstrong (2001) have also been taken into account in this work, namely: (i) structuring of the problem; (ii) information gathering; (iii) forecasting methods implementation; and (iv) evaluation of the forecasting method.
As stated by Martins and Werner (2012), it is necessary to analyze a wide range of techniques and verify which one provides the best measures of accuracy for obtaining a better forecast. For this purpose, in this study three individual techniques and fourteen combination methods have been comparatively evaluated using three different measures of accuracy.
The proposed systematic approach can be presented as a sequence of steps for its implementation. Figure 1 presents a flowchart of the systematic approach aimed at solving the problem of identifying individual forecasting techniques and their combinations, which are capable of adequately forecasting the water withdrawal volume for urban use.
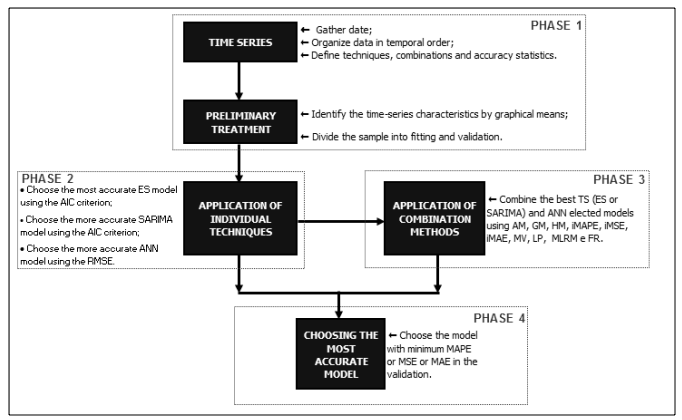
Source: Elaborated by the authors.
Figure 1 – Structuring Phases of the Proposed Systematic Approach
The proposed systematic approach is divided into four phases. Each phase is divided into stages, with a noticeable characteristic of phase 3 that is divided into 14 stages. In the preliminary phase, named Phase 1, data from a data base were gathered, filtered, organized in time and validated such that one is capable of obtaining forecasting models. The individual techniques, the combination methods, and the adopted measures of accuracy for the identification of model(s) that are adequate for each series of study are defined in this phase. Finally, still in this phase, the series characteristics are identified as tendency and seasonality, and the sample is divided into fitting and validation.
Phase 2 consists in the identification of the models for the exponential smoothing (ES), SARIMA and ANN. Akaike information criterion (AIC) was chosen among the different criteria that can be used for the process of selecting the best model in ES and ARIMA classes (Snyder & Order, 2009). On the other hand, RMSE was used to select the best ANN structure. Phase 2 is divided into three stages:
In phase 3, forecast combination methods are executed with values obtained from phase 2, assigning values to the individual techniques. The first stage of this phase consists in the choice of the best Statistical Technique - TS (ES or SARIMA) by the lowest MAPE in validation for each time series. The combination methods have been detailed in section 2.2, and the weights are: (i) of equal values (arithmetic mean, Comb AM); (ii) geometric mean (Comb GM); (iii) harmonic mean (Comb HM); (iv) inversely proportional to MAPE (Comb iMAPE); (v) inversely proportional to the MSE (Comb iMSE); (vi) inversely proportional to the MAE (Comb iMAE); (vii) obtained through the minimum variance with correlation (Comb MV ); (viii) obtained through the uncorrelated minimum variance (Comb MV ); (ix) obtained through Linear Programming (LP) and by minimizing the MAPE (Comb LP min MAPE); (x) obtained through LP while minimizing the MSE (Comb LP min MSE); (xi) through LP and by minimizing the MAE (Comb LP min MAE); (xii) through the Multiple Linear Regression Model (Comb MLRM) with intercept (Comb MLRM1); (xiii) through MLRM without intercept (Comb MLRM2); and (xiv) through relative frequency with the least absolute error (Comb FR).
Finally, in phase 4, by using the last part of the historical data reserved for the validation of each modeling (technique or method), the most accurate model is elected by the performance measures using MAPE, MSE, or MAE. It is thus possible to evaluate if the forecasts performed by individual models or their combinations can generate better forecasts.
The use of an evaluation criterion is necessary to assess and compare the predictive performance of the forecasts. In this study, three types of quantitative evaluation criteria are used: MAPE, MSE and MAE. It is highlighted that each one of those accuracy statistics is based on errors of one-step-ahead forecasting, that are calculated by the difference between the observed value at time and the predicted value at time for the time .
The structuring of the data base was performed in MS-Excelâ software. The software Statgraphics Centurion XVIâ was used for the modeling of data using ES and SARIMA techniques, as well as the statistical analysis of parameters significance of the model, the fitting quality (residues analysis) and the accuracy measures. On the other hand, the application developed in software MATLABÒ identified a suitable structure for ANN.
MS-Excelâ scripts to process spreadsheets have been written for the several proposed combinations. In addition, resources are used, like (i) the function "solver" to estimate weights with LP for the three methods (min MAPE, min MSE, and min MAE); and (ii) the function "data analysis – regression" to estimate the weights using MLRM for both methods (with and without intercept). The next section presents the main results from the systematic application of the proposal to evaluate the performance of forecasting models to forecast the water volume withdrawal in Brazilian cities.
To validate the proposed systematic approach, the methodology was applied to data from 10 cities of the micro-region in the surrounding area of Pato Branco City, in the southwestern region of the state of Paraná, Brazil. The main phases used to analyze each time series following the proposed methodology were: (i) data gathering in the Water and Sanitation Company of Paraná (SANEPAR), which guaranteed the reliability of the information; (ii) representation and analysis of each series being studied by inspecting the behavior of the time plot, confirming that the most prominent features of the series are the growing and seasonal tendency over the years; (iii) individual modeling by ES, SARIMA and ANN; (iv) execution of the forecast combinations; and (v) comparison of the accuracy measures. Thus, three measures of performance for each modeling were calculated, resulting in a total of 510 (3x10x17).
In sections 4.1 to 4.3, the phases of the described systematic approach of section 3 are presented. As each city has its own distinguishing characteristics, forecasts were directed to each one in an individual manner, trying to represent the tendency behavior and seasonality by means of ES, SARIMA, ANN models, and the 14 resulting combinations. In section 4.4, the obtained results are discussed.
During the last decade it has been observed from the available data for the 10 cities that they had different human development, social, and economic indexes, as shown in Table 2. The results of City's Human Development Index (CHDI) and FIRJAN Index of City Development (FICD) show the differences among the studied cities. For the analyzed period, the annual geometric population growth rate was positive for 5 cities and negative for the others. Population in those cities varied from 3,293 to 72,370 inhabitants. The annual growth rate of water connections was positive for the cities studied in the research.
Table 2: Characterization of the cities in the case-study
City |
CHDI1 (2010) Value |
CHDI1 (2010) Position |
FICD2 (2012) Value |
FICD2 (2012) Position |
Growth Rate N.Con.4 |
Urban Rate (2010) |
Growth Rate Pop.3 |
Number of inhabitants3 |
|
2000 |
2010 |
||||||||
Pato Branco |
0.782 |
113ª |
0.8256 |
208ª |
4,26% |
94,09% |
1.52% |
62.234 |
72.370 |
Mariópolis |
0.698 |
1.969ª |
0.7026 |
1.657ª |
3,74% |
71,29% |
0.41% |
6.017 |
6.268 |
Clevelândia |
0.694 |
2.078ª |
0.6915 |
1.892ª |
1,73% |
85,63% |
-0.62% |
18.338 |
17.240 |
Palmas |
0.660 |
2.898ª |
0.6510 |
2.733ª |
2,37% |
92,81% |
2.11% |
34.819 |
42.888 |
Mangueirinha |
0.688 |
2.224ª |
0.6713 |
2.302ª |
5,11% |
49,21% |
-0.41% |
17.760 |
17.048 |
Coronel Vivida |
0.723 |
1.217ª |
0.7300 |
1.128ª |
4,80% |
70,99% |
-0.69% |
23.306 |
21.749 |
Chopinzinho |
0.740 |
764ª |
0.7428 |
920ª |
3,53% |
63,55% |
-0.43% |
20.543 |
19.679 |
Itapejara do Oeste |
0.731 |
993ª |
0.6311 |
3.132ª |
3,38% |
66,35% |
1.40% |
9.162 |
10.531 |
Bom Sucesso do Sul |
0.742 |
719ª |
0.7502 |
816ª |
3,54% |
47,97% |
-0.30% |
3.392 |
3.293 |
Vitorino |
0.702 |
1.842ª |
0.7419 |
938ª |
3,01% |
61,16% |
0.36% |
6.285 |
6.513 |
Source: Elaborated by the authors with data from PNUD1(2013), FIRJAN2(2012), IBGE3(2014) and IPARDES4(2012).
Data over a time span used in this study were gathered in the regional unit of the Water and Sanitation Company of Paraná (SANEPAR). These data were chosen because they represent real values being organized in time without the need to fill the data set with intermediate values. Figure 2 presents the historical behavior of the withdrawn volume of water in each of the 10 cities that served as a basis for the application of the proposed systematic approach. As expected, the plot of the historical time series revealed a growing tendency and a seasonal behavior in the withdrawn volume of water, even though the population growth rate was negative in some cities.
For each one of the series, both the historical average level and the linear fit were determined with a regression equation (y = ax + b) and the coefficient of determination (R2). Moreover, the figure places an emphasis on the division that occurred in the gathered samples, which had one data set to fit each one of the models in the scope of this work and another data set for its validation. The sample is formed by 132 observations (11 years) for each city and was divided into a fitting set (120 observations) and a validation set (12 observations). Following the classification used by Makridakis and Hibon (2000), the planning horizon is a medium-term one if it is a 4- to 12- step-ahead forecast, and in this case, its horizon is twelve months.
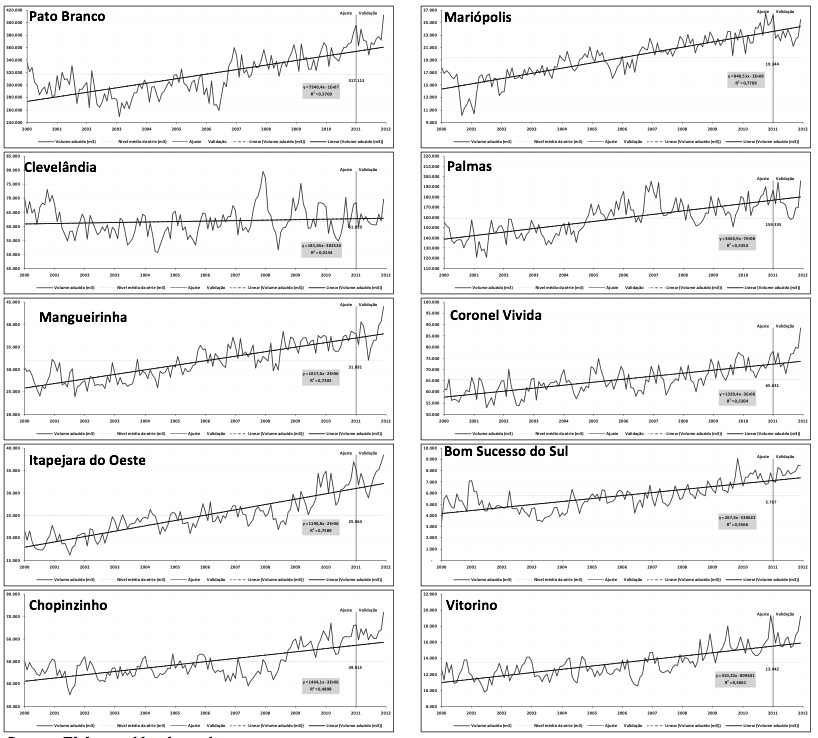
Source: Elaborated by the authors.
Figure 2: Characterization of time series of the withdrawn volume in the cities
The statistical software determined the most accurate models of ES and SARIMA classes. The individual models used in the combinations were considered adequate, as they have significant coefficients and uncorrelated residues. The best statistical technique (ST) was chosen for each city by MAPE validation. The computational application developed in MATLABÒ has identified an adequate structure of ANN for each assessed city. The main results for the individual techniques are shown in Table 3, which highlights the model identified for each series. The programmed spreadsheet permitted the proposed combinations. Moreover, Table 4 presents a summary of results obtained with the combinations. These results are analyzed in Section 4.4.
An initial observation is that all the individual techniques presented appropriate values for MAPE (below 8%). The methods of ES (ESHW or SES, the only ones elected from among those evaluated) were more accurate by 50% in the evaluated cities and also obtained the best average performance measured by validation MAPE. Moreover, SARIMA models also showed promising results, being superior in 40% of the cities, with average MAPE close to those obtained by ES models. On the other hand, the technical artificial intelligence (TAI) evaluated (ANN) was more accurate only in one city and had the lowest average MAPE in comparison with TS.
Table 3: Identified Model and comparison of the performance of individual techniques by MAPE
Technique |
Statistic (TS) |
Statistic (TS) |
Artificial Intelligence (TAI) |
Best |
City |
ES (MAPE validation) |
SARIMA (MAPE validation) |
ANN (MAPE validation) |
MAPE |
Pato Branco |
ESHW with a = 0.6422, b = 0.0330 and g = 0.2798 MAPE = 2.877% |
(2, 1, 2)x(1, 1, 2)12 with constant MAPE = 1.885% |
n = 10; eg = 0.01, sc = 0.99 MAPE = 3.130% |
SARIMA |
Mariópolis |
ESHW with a = 0.8049, b = 0.0490 and g = 0.3253 MAPE = 4.649% |
(0, 0, 2)x(3, 1, 3)12 with constant MAPE = 4.408% |
n = 11, eg = 0.01, sc = 0.75 MAPE = 4.476% |
SARIMA |
Clevelândia |
SES with a = 0.7794 MAPE = 3.056% |
(1, 0, 0)x(2, 1, 3)12 without constant MAPE = 3.392% |
n = 12, eg = 0.03, sc = 0.63 MAPE = 3.475% |
ES |
Palmas |
ESHW with a = 0.6057, b = 0.0089 and g = 0.3041 MAPE = 3.883% |
(3, 0, 0)x(4, 1, 4)12 with constant MAPE = 6.957% |
n = 9, eg = 0.01, sc = 0.67 MAPE = 3.685% |
ANN |
Mangueirinha |
ESHW with a = 0.4788, b = 0.0079 and g = 0.1355 MAPE = 5.093% |
(1, 0, 0)x(2, 1, 3)12 with constant MAPE = 3.610% |
n = 12, eg = 0.01, sc = 0.83 MAPE = 5.217% |
SARIMA |
Coronel Vivida |
SES with a = 0.5486 MAPE = 2.980% |
(1, 0, 0)x(1, 1, 4)12 with constant MAPE = 3.491% |
n = 9, eg = 0.01, sc = 3.87 MAPE = 4.494% |
ES |
Chopinzinho |
SES with a = 0.6893 MAPE = 2.957% |
(0, 1, 1)x(1, 0, 3)12 without constant MAPE = 4.501% |
n = 9, eg = 0.03, sc = 3.65 MAPE = 4.275% |
ES |
Itapejara do Oeste |
SES with a = 0.5064 MAPE = 3.262% |
(2, 1, 3)x(2, 1, 3)12 without constant MAPE = 2.701% |
n = 8, eg = 0.01, sc = 1.87 MAPE = 3.465% |
SARIMA |
Bom Sucesso do Sul |
ESHW with a = 0.3272, b = 0.0251 and g = 0.0672 MAPE = 3.413% |
(2, 1, 2)x(1, 1, 2)12 with constant MAPE = 4.737% |
n = 12, eg = 0.01, sc = 0.95 MAPE = 5.036% |
ES |
Vitorino |
ESHW with a = 0.3803, b = 0.0001 and g = 0.1405 MAPE = 3.516% |
(1, 1, 1)x(1, 1, 4)12 without constant MAPE = 3.615% |
n = 11, eg = 0.03, sc = 3.55 MAPE = 7.853% |
ES |
Average performance |
MAPE = 3.569% |
MAPE = 3.930% |
MAPE = 4.511% |
ES |
Source: Elaborated by the authors.
Table 4: Performance of combinations measured by MAPE
Models |
Average performance (10 cities) |
Comb AM |
3.436% |
Comb GM |
3.448% |
Comb HM |
3.460% |
Comb IMAPE |
3.402% |
Comb IMSE |
3.426% |
Comb IMAE |
3.402% |
Comb MV (r ¹ 0) |
3.426% |
Comb MV (r = 0) |
3.447% |
Comb LP min MAPE |
3.730% |
Comb LP min MSE |
3.642% |
Comb LP min MAE |
3.732% |
Comb MLRM1 |
3.585% |
Comb MLRM2 |
3.667% |
Comb FR |
3.440% |
Source: Elaborated by the authors.
To evaluate the individual performance of each model (technique or method), the best model for each city was identified according to adopted accuracy measures. These results are listed in Table 5. For the proposed phase application, the MAPE criterion of the validation was adopted to choose the most accurate individual model.
Table 5: Determination of the most accurate model by the MAPE criterion
City |
Chosen Method/Technique |
MAPE |
Pato Branco |
SARIMA |
1.885% |
Mariópolis |
Comb AM |
3.976% |
Clevelândia |
Comb iMAPE |
2.803% |
Palmas |
Comb MLRM1 |
3.625% |
Mangueirinha |
Comb MLRM1 |
3.488% |
Coronel Vivida |
Comb MV (r = 0) |
2.940% |
Chopinzinho |
ES |
2.957% |
Itapejara do Oeste |
Comb MLRM1 |
2.309% |
Bom Sucesso do Sul |
ES |
3.413% |
Vitorino |
ES |
3.516% |
Source: Elaborated by the authors.
According to MAPE criterion, the individual techniques were improved in 40% of the evaluated cases. On the other hand, the used combination methods were more accurate in 60% of the evaluated series. In addition, while the individual techniques produced MAPE lower than 8%, the choice of the most accurate model (individual technique or combination method) generated MAPE lower than 4% for the 10 cities.
Section 4.3 ends the application cycle of the proposed methodology and shows how the managing board in a water and sanitation company could have forecasts for a whole micro-region in a horizon of 12 months with MAPE below 4%. The managing plan for the following year could be done based on a good forecasting system. However, the company should have an automatized systematic approach or there should be an employee with specific knowledge to select the presented individual models. One question may be raised in this situation: "Would there be a technique/method that could be directly applied and produce good results?" In the following section this discussion is developed on an analysis using the descriptive statistics of the results.
The first analysis consisted in the identification of frequency with which each model was selected (individual technique or combination method) for the 10 cities and each measure of accuracy: MAPE, MSE and MAE, as demonstrated in Table 6.
Table 6: Summary of the performance in the validation of the evaluated techniques and methods of combination
| City | MAPE |
MSE |
MAE |
Pato Branco |
SARIMA |
SARIMA |
SARIMA |
Mariópolis |
Comb AM |
Comb FR |
Comb AM |
Clevelândia |
Comb iMAPE |
Comb MV (r = 0) |
Comb iMAPE |
Palmas |
Comb MLRM1 |
Comb MLRM1 |
Comb MLRM1 |
Mangueirinha |
Comb MLRM1 |
Comb MLRM1 |
Comb MLRM1 |
Coronel Vivida |
Comb MV (r = 0) |
Comb MV (r = 0) |
Comb MV (r = 0) |
Chopinzinho |
ES |
Comb MLRM1 |
ES |
Itapejara do Oeste |
Comb MLRM1 |
Comb FR |
Comb MLRM1 |
Bom Sucesso do Sul |
ES |
Comb iMSE |
ES |
Vitorino |
ES |
ES |
ES |
Source: Elaborated by the authors.
The ES technique and the combination methods "iMAPE, iMSE, iMAE, MV (r ¹ 0) and MV (r = 0)" reached a better average performance in the validation, measured by MAPE, and an even higher average performance was obtained in the fitting. On the other hand, validation had a worse performance than the fitting for SARIMA and ANN models, Comb AM, Comb GM, Comb HM, Comb LP min MAPE, Comb LP min MSE, Comb LP min MAE, Comb MLRM1 and Comb MLRM2.
Next, an analysis of absolute and relative frequencies was performed. It had the goal of identifying the frequency at which a forecast model presents the best average accuracy evaluated for each series of data. Because of that, the number of times that each model obtained the best performance in the validation was registered, with the results listed in Table 7.
Table 7: Frequencies and percentages of the measures of accuracy in the validation
Accuracy Measure |
MAPE |
MSE |
MAE |
TOTAL |
||||
Models |
Freq |
% |
Freq |
% |
Freq |
% |
Freq |
% |
SE |
3 |
30% |
1 |
10% |
3 |
30% |
7 |
23.33% |
SARIMA |
1 |
10% |
1 |
10% |
1 |
10% |
3 |
10% |
ANN |
0 |
0% |
0 |
0% |
0 |
0% |
0 |
0% |
Comb AM |
1 |
10% |
0 |
0% |
1 |
10% |
2 |
6.67% |
Comb GM |
0 |
0% |
0 |
0% |
0 |
0% |
0 |
0% |
Comb HM |
0 |
0% |
0 |
0% |
0 |
0% |
0 |
0% |
Comb iMAPE |
1 |
10% |
0 |
0% |
1 |
10% |
2 |
6.67% |
Comb iMSE |
0 |
0% |
1 |
10% |
0 |
0% |
1 |
3.33% |
Comb iMAE |
0 |
0% |
0 |
0% |
0 |
0% |
0 |
0% |
Comb MV (r ¹ 0) |
0 |
0% |
0 |
0% |
0 |
0% |
0 |
0% |
Comb MV (r = 0) |
1 |
10% |
2 |
20% |
1 |
10% |
4 |
13.33% |
Comb LP min MAPE |
0 |
0% |
0 |
0% |
0 |
0% |
0 |
0% |
Comb LP min MSE |
0 |
0% |
0 |
0% |
0 |
0% |
0 |
0% |
Comb LP min MAE |
0 |
0% |
0 |
0% |
0 |
0% |
0 |
0% |
Comb MLRM1 |
3 |
30% |
3 |
30% |
3 |
30% |
9 |
30% |
Comb MLRM2 |
0 |
0% |
0 |
0% |
0 |
0% |
0 |
0% |
Comb FR |
0 |
0% |
2 |
20% |
0 |
0% |
2 |
6.67% |
TOTAL |
10 |
100% |
10 |
100% |
10 |
100% |
30 |
100% |
Source: Elaborated by the authors.
On the comparison between the individual techniques and the combination methods for the three criteria (MAPE, MSE and MAE), we highlight: (i) individual techniques (10/30), with SARIMA (3/30) and ES (7/30); (ii) combinations (20/30); (iii) best TS (ES or SARIMA): 10/30 (33.33%); (iv) Comb MRLM1, that is, with intercept: 9/30 (30%); (v) Comb VM (p = 0): 4/30 (13.33%); (iv) Comb AM: 2/30 (6.67%); (vii) Comb iMAPE: 2/30 (6.67%); (viii) Comb FR: 2/30 (6.67%); (ix) Comb iMSE: 1/30 (3.33%); and (x) other evaluated techniques (ANN and other combinations) that were less accurate in all the cases studied.
These results show that the combinations of methods generally produce more accurate results than the individual predictors. The unanimity occurred in the cities of Pato Branco (SARIMA), Palmas and Mangueirinha (Comb MLRM1), Coronel Vivida (Comb MV p = 0) and Bom Sucesso do Sul (SE). In this case, the Comb MLRM1 method (30%) was the one which presented a better performance concerning the other three adopted accuracy measures. It is also worth mentioning the ES technique (23.33%).
We observe that MAPE and MSE accuracy measurements always pointed to the same model. For MAPE and MAE criteria, the individual techniques were superior in 40% of the evaluated cases with a proportion of 30% to ES and 10% to SARIMA, while the combinations were better in 60% of the experiments. On the other hand, for MSE criterion, ES and SARIMA techniques were each successful in 10% of the cases, while the combinations were more accurate in 80% of the cases.
As previously cited, three measures were used in this study as a way to measure the performance of the evaluated modeling. However, the frequency at which a model is chosen does not demonstrate unanimity. For comparison of different series, MAPE statistics are the most used measures of accuracy (Kahn, 1998; Goodwin & Lowton, 1999).
In this sense, Table 8 presents the results for this specific measure of accuracy. However, analysis will be performed for all the referred measures. This table presents descriptive statistics of central tendency and dispersion of validation MAPE to evaluate the global performance observed in the modeling and combinations. The best results for each statistics are in bold format.
Observing results shown in Table 8 allows one to infer that the "worst" model (technique or method) had a maximum MAPE which was less than 8% (7.853%) in all the 10 studied cities. For all the evaluated measures of accuracy, the best TS had a superior average performance for the evaluated statistics: minimum, maximum, mean and standard deviation.
Table 8: Performance measured by the validation MAPE
Statistics |
||||
Models |
Minimum |
Maximum |
Mean |
Standard- Deviation |
ANN |
3.130% |
7.853% |
4.509% |
1.366% |
ES |
2.877% |
5.093% |
3.569% |
0.758% |
SARIMA |
1.885% |
6.957% |
3.930% |
1.364% |
Best TS |
1.885% |
4.408% |
3.297% |
0.667% |
Comb AM |
2.312% |
4.926% |
3.436% |
0.805% |
Comb GM |
2.306% |
4.976% |
3.448% |
0.819% |
Comb HM |
2.300% |
5.025% |
3.460% |
0.832% |
Comb IMAPE |
2.258% |
4.768% |
3.402% |
0.776% |
Comb IMSE |
2.232% |
4.693% |
3.426% |
0.810% |
Comb IMAE |
2.258% |
4.768% |
3.402% |
0.776% |
Comb MV (r ¹ 0) |
2.232% |
4.695% |
3.426% |
0.810% |
Comb MV (r = 0) |
2.196% |
4.510% |
3.447% |
0.805% |
Comb LP min MAPE |
2.498% |
6.065% |
3.730% |
1.125% |
Comb LP min MSE |
2.428% |
5.873% |
3.642% |
1.094% |
Comb LP min MAE |
2.498% |
6.084% |
3.732% |
1.123% |
Comb MLRM1 |
2.309% |
5.639% |
3.585% |
1.067% |
Comb MLRM2 |
2.367% |
5.868% |
3.667% |
1.088% |
Comb FR |
2.402% |
4.722% |
3.440% |
0.788% |
Minimum |
1.885% |
4.408% |
3.297% |
0.667% |
Maximum |
3.130% |
7.853% |
4.509% |
1.366% |
Mean |
2.364% |
5.379% |
3.593% |
0.948% |
Standard-Deviation |
0.274% |
0.922% |
0.274% |
0.203% |
Individual (average performance) |
2.631% |
6.634% |
4.002% |
1.163% |
Combinations (average performance) |
2.336% |
5.157% |
3.517% |
0.910% |
Difference: individual versus combinations |
-11.20% |
-22.26% |
-12.12% |
-21.77% |
Source: Elaborated by the authors.
According to MAPE, the best TS (ES or SARIMA) had the best average performance, the lowest standard deviation, and the lowest coefficient of variation. In the evaluated context, it is the best forecast technique, even when compared to fourteen combinations. On the other hand, TAI (ANN) had the worst performance in average and standard deviation categories. Globally, the combinations did not generate, on average, more accurate results than the best TS (ES or SARIMA). However, the average performance of individual methods was inferior to those of combinations as shown in Table 8.
The best general performance in those 10 cities, according to MAPE variability criterion in validation, was the most accurate model of ES or SARIMA, for it obtained the lowest standard deviation (0.667%) and had the best average (3.297%). On the other hand, the ANN model obtained MAPE maximum average (4.509%) and the highest average standard deviation (1.366%), resulting in the "worst" evaluated model in this aspect.
The best techniques measured by average MSE of the validation had the most accurate model of ES or SARIMA with the best performance (Appendix I). Similar results occurred for MAE accuracy measurements of validation statistics concerning mean and standard deviation (Appendix I).
Comparing the results obtained in this study with data from M-Competition (Makridakis & Hibon, 2000; Nikolopoulos et al., 2011b), the following points have been ratified:
Small differences, which were evaluated by the position and dispersion statistics among the evaluated models, indicate that any one of such models is likely to be used. However, given the simplicity, performance, and significance, the ES model is the most usable to estimate the withdrawn volume. This is particularly important if there is no specialist or dedicated professional in the water company with knowledge to apply the proposed methodology.
The operationalization of strategies in the planning and control of production is strongly attached to the existence of an effective forecasting system. Sustainability, knowledge of historical reality, and future developments must be known for planning to be implemented. In this sense, all the evaluated models generate adequate forecasts in agreement with the scope of this work. Furthermore, the combinations increase the accuracy of forecasts.
As a first result, predominant frequency is highlighted, at which the results from combinations of forecasts presented a superior performance when compared with individual forecasts, since the worst MAPE was reduced from 8% to 4%.
From the results, it was demonstrated that all the evaluated models are adequate to produce a volume withdrawal forecast in a horizon of 12 months. The best general performance in the 10 cities, according to the variability of validation MAPE, was the best statistical techniques (MAPE = 3.297% and standard deviation = 0.667%). In the practical context of water and sanitation companies, they can use an individual ES technique with good results (MAPE = 3.569% and standard deviation = 0.758%).
The classification and choice of the best method depends on the forecast horizon; that is, a few methods have a better performance for a determined horizon and are worse for others (Makridakis & Hibon, 2000). Thus, the obtained results should not be used for planning horizons which are not contemplated in this study. However, a systematic approach can be used without significant changes in it.
The research conclusion allows one to list some future works like: (i) the application of the proposed systematic approach in a set with more cities, in different regions and with larger populations; and (ii) the performance evaluation for a wider forecast horizon from 2 to 5 years.
Authors thank the Water and Sanitation Company of Paraná (SANEPAR) for providing data and support in the development of this research.
[1] Adamowski J. 2008. Peak Daily Water Demand Forecast Modeling Using Artificial Neural Networks. Journal of Water Resources Planning and Management, 134:119-128.
[2] Almutaz I, Ajbar A, Khalid Y & Ali E. 2012. A probabilistic forecast of water demand for a tourist and desalination dependent city: Case of Mecca, Saudi Arabia. Desalination, 294:53–59.
[3] ANA. Agência Nacional de Águas. Conjuntura dos recursos hídricos no Brasil. Special Edition. Brazil. Available at http://arquivos.ana.gov.br/imprensa/arquivos/Conjuntura2012.pdf. Accessed at 24 nov. 2012.
[4] Andrawis RR, Atiya AF & El-Shishiny H. 2011. Combination of long term and short term forecasts, with application to tourism demand forecasting. International Journal of Forecasting, 27(3):870-886.
[5] Armstrong JS. 2001. Principles of Forecasting: A handbook for researchers and practitioners. New York: Kluwer Academic Publishers.
[6] Azadeh A, Neshat N & Hamidipour H. 2012. Hybrid Fuzzy Regression – Artificial Neural Network for Improvement of Short-Term Water Consumption Estimation and Forecasting in Uncertain and Complex Environments: Case of a Large Metropolitan City. Journal of Water Resources Planning and Management, 138:71-75.
[7] Bates JM & Granger CWJ. 1969. The Combining of Forecasts. Operational Research Quarterly, 20(4):451-468.
[8] Caiado J. 2010. Performance of combined double seasonal univariate time series models for forecasting water demand. Journal of Hydrologic Engineering, 15(3): 215-222.
[9] Calôba GM, Calôba LP & Saliby E. 2002. Cooperação entre redes neurais artificiais e técnicas clássicas para previsão de demanda de uma série de vendas de cerveja na Austrália. Pesquisa Operacional, v.22, n.3, p.345-358.
[10] Campisi-Pinto S, Adamowski J & Oron G. 2012. Forecasting UrbanWater Demand Via Wavelet-Denoising and Neural Network Models. Case Study: City of Syracuse, Italy. Water Resour Management, 26:3539–3558.
[11] Clemen RT. 1989. Combining forecasts: A review and annotated bibliography. International Journal of Forecasting, 5:559–583.
[12] Dias G J C. 2006. Planejamento estratégico de um centro de distribuição: uma aplicação de redes neurais artificiais de funções de bases radiais para previsão de séries temporais. Dissertação de mestrado. Universidade Federal do Paraná.
[13] Faria F & Mubwandarikwa, E. 2008. The Geometric Combination of Bayesian Forecasting, Journal of Forecasting, 27/6:519-535.
[14] Firat M, Turan ME & Yurdusev MA. 2010. Comparative analysis of neural network techniques for predicting water consumption time series. Journal of Hydrology, 384:46–51.
[15] FIRJAN. Federação das Indústrias do Rio de Janeiro. Índice Firjan de Desenvolvimento Municipal. Available at http://www.firjan.org.br/ifdm/downloads/. Accessed at 12 dec. 2012.
[16] Flores BE & White EM. 1988. A Framework for the Combination of Forecasts. Journal of the Academy of Marketing Science, 16(3-4):95-103.
[17] Ghiassi M, Zimbra D & Saidane H. 2008. Urban Water Demand Forecasting with a Dynamic Artificial Neural Network Model. Journal of Water Resources Planning and Management, 134:138-146.
[18] Goodwin P & Lawton R. 1999. On the asymmetry of the symmetric MAPE. International Journal of Forecasting, 15:405-408.
[19] Granger CWJ & Ramanathan R. 1984. Improved Methods of Forecasting. Journal of Forecasting, 3:197-204.
[20] Herrera M, Torgo L, Izquierdo J & Pérez-García R. 2010. Predictive models for forecasting hourly urban water demand. Journal of Hydrology, 387:141–150.
[21] Hibon M & Evgeniou T. 2005. To combine or not to combine: selecting among the forecasts and their combinations. International Journal of Forecasting, 21(1):15-24.
[22] IBGE. Instituto Brasileiro de Geografia e Estatística. IBGE Cidades @. Available in http://www.ibge.gov.br/cidadesat/topwindow.htm?1. Accessed at 12 dec. 2014.
[23] IPARDES. Instituto Paranaense de Desenvolvimento Econômico e Social. Caderno Estatístico por Município. Available at http://www.ipardes.gov.br/cadernos/. Accessed at 12 dec. 2012.
[24] Kahn KB. 1998. Benchmarking sales forecasting performance measures. The Journal of Business Forecasting Methods & Systems, 17(4):19-23.
[25] Konig AJ, Franses PH, Hibon M & Stekler HO. 2005. The M3-Competition: Statistical tests of the results. International Journal of Forecasting, 21: 397–409.
[26] Makridakis S & Hibon M. 2000. The M3-Competition: results, conclusions and implications. International Journal of Forecasting, 16: 451-476.
[27] Makridakis S, Wheelwright SC & Hyndman RJ. 1998. Forecasting, Methods and Applications. Third Edition. New York: John Wiley & Sons.
[28] Martins V & Werner L. 2012. Forecast combination in industrial series: A comparison between individual forecasts and its combinations with and without correlated errors. Expert Systems with Applications, 39:11479–11486.
[29] MATLAB. 2010. Version 2010b. User's Guide.
[30] Mohamed MM & Al-Mualla AA. 2010. Water demand forecasting in Umm Al-Quwain using the constant rate model. Desalination, 259:161–168.
[31] Morettin P A & Toloi C M C. 2006. Análise de Series Temporais. 2. ed. São Paulo: Editora Edgard Blucher.
[32] Newbold P & Bos T. 1994. Introductory Business & Economic Forecasting. Second edition, South-Western Publishing, Cincinnati. Ohio.
[33] Nikolopoulos K, Makridakis S, Assimakopoulos V & Syntetos A. 2011a. The M4 Competition. The Operational Research Society Conference 2011 – OR53, September 6-8 2011, East Midlands Conference Centre, Nottingham, UK.
[34] Nikolopoulos K, Makridakis S, Assimakopoulos V & Syntetos A. 2011b. The M4 Competition: Facts, Innovations and the way Forward. 31th Annual International Symposium on Forecasting - ISF 2011, June 26-29. 2011, Prague, Check Republic.
[35] Panagiotopoulos A. 2011. Optimising Time Series Forecasts Through Linear Programming. University of Nottingham. Thesis PhD. 205p.
[36] PNUD. Programa das Nações Unidas para o Desenvolvimento. 2010. Ranking do IDH dos Municípios do Brasil. Available at http://atlasbrasil.org.br/2013/ranking. Accessed at 17 may 2014.
[37] Qi C & Chang N. 2011. System dynamics modeling for municipal water demand estimation in an urban region under uncertain economic impacts. Journal of Environmental Management, 92:1628-1641.
[38] Snyder RD & Ord J K. 2009. Exponential Smoothing and the Akaike Information Criterion, Monash Econometrics and Business Statistics. Working Papers, 4/09 working paper, Monash University.
[39] Souza GP. 2008. Método para estruturar a integração de previsões utilizando a técnica Delphi. Tese de doutorado. Universidade Federal de Santa Catarina.
[40] Statgraphics Centurion XVI. 2014. Version 16.1.17. User's Guide.
[41] Stock JH & Watson MW. 1999. A comparison of linear and nonlinear univariate models for forecasting macroeconomic time series. In Engle RF, White H (eds). Cointegration, Causality and Forecasting: A Festschrift for Clive W.J. Granger. Oxford University Press: Oxford; 1–44.
[42] Stock JH & Watson MW. 2004. Combination forecasts of output growth in a seven-country data set. Journal of Forecasting, 23: 405–430.
[43] VWNA. Veolia Water North America. Finding the blue path for a sustainable economy. Chicago, EUA. Available in http:// www.veoliawaterna.com. Accessed at 24 nov. 2012.
[44] Werner L & Ribeiro JLD. 2006. Modelo composto para prever demanda através da integração de previsões. Revista Produção, 16(3):493-509.
[45] Werner L. 2012. Na busca pelo melhor método de combinação de previsões por meio do uso de análise de correlação e análise de cluster. In: II Congresso Brasileiro de Engenharia de Produção. Ponta Grossa, PR, Brasil, 28 a 30 de novembro de 2012.
[46] Wu Y, Liu B, Li M, Tang k & Wub Y. 2013. Prediction of CO2 solubility in polymers by radial basis function artificial neural network based on chaotic self-adaptive particle swarm optimization and fuzzy clustering method. Chinese Journal of Chemistry, 31: 1564-1572.
[47] Yasar A, Bilgili M & Simsek E. 2012. Water Demand Forecasting Based on Stepwise Multiple Nonlinear Regression Analysis. Arabian Journal for Science and Engineering, 37:2333–2341.
[48] Zhai Y, Wang J, Teng Y & Zuo R. 2012. Water demand forecasting of Beijing using the Time Series Forecasting Method. J. Geogr. Sci, 22(5): 919-932.
APPENDIX I - COMPLEMENTARY RESULTS
Table 1: Performance measured by the validation MSE
Statistics |
||||
Models |
Minimum |
Maximum |
Mean |
Standard- Deviation |
ANN |
312,992.46 |
172,693,699.00 |
28,678,478.36 |
54,524,163.40 |
ES |
120,253.06 |
201,694,794.33 |
30,580,878.51 |
64,674,971.19 |
SARIMA |
214,549.46 |
168,127,388.75 |
28,791,089.63 |
55,418,37040 |
Best TS |
120,253.06 |
85,920,417.92 |
18,545,578.63 |
33,720,238.28 |
Comb AM |
147,473.44 |
104,248,463.12 |
19,662,940.17 |
36,035,105.95 |
Comb GM |
147,881.34 |
103,981,506.80 |
19,669,830.35 |
35,974,776.37 |
Comb HM |
148,364.34 |
103,719,798.21 |
19,678,060.19 |
35,915,962.26 |
Comb IMAPE |
119,855.39 |
99,173,246.53 |
19,398,169.79 |
36,035,105.95 |
Comb IMSE |
113,956.72 |
96,990,069.73 |
19,565,458.20 |
35,049,456.46 |
Comb IMAE |
120,417.35 |
99,135,412.69 |
19,393,257.93 |
34,832,413.80 |
Comb MV (r ¹ 0) |
113,971.70 |
97,006,476.03 |
19,561,774.28 |
35,038,735.98 |
Comb MV (r = 0) |
119,255.25 |
94,319,587.24 |
19,882,757.45 |
34,825,283.02 |
Comb LP min MAPE |
312,992.46 |
124,439,896.00 |
21,903,125.91 |
34,596,082.58 |
Comb LP min MSE |
307,291.67 |
117,902,563.60 |
20,982,825.45 |
41,443,484.45 |
Comb LP min MAE |
312,992.46 |
124,439,991.76 |
21,902,348.32 |
39,681,438.56 |
Comb MLRM1 |
306,216.40 |
114,626,256.63 |
20,380,671.87 |
41,443,415.46 |
Comb MLRM2 |
307,287.50 |
117,315,211.21 |
21,010,555.16 |
38,601,664.20 |
Comb FR |
188,884.91 |
114,469,272.23 |
20,541,686.69 |
38,676,747.72 |
Minimum |
113,956.72 |
85,920,417.92 |
18,545,578.63 |
33,720,238.28 |
Maximum |
312,992.46 |
201,694,794.33 |
30,580,878.51 |
64,674,971.19 |
Mean |
213,956.40 |
120,386,424.83 |
21,875,672.73 |
41,006,187.94 |
Standard-Deviation |
91,261.83 |
30,574,131.05 |
3,586,999.88 |
8,523,224.09 |
Individual (average performance) |
215,931.66 |
180,838,627.36 |
29,350,148.83 |
58,205,835.00 |
Combinations (average performance) |
211,213.31 |
109,138,790.74 |
20,407,123.41 |
37,604,023.64 |
Difference: individual versus combinations |
-2.19% |
-39.65% |
-30.47% |
-35.39% |
Source: Elaborated by the authors. Note: Best mean and standard deviation
for the best TS (ES or SARIMA), according to the MSE criterion.
Table 2: Performance measured by the validation MSE
Models |
Statistics |
|||
Minimum |
Maximum |
Mean |
Standard- Deviation |
|
ANN |
386.57 |
11,730.75 |
3,268.12 |
3,449.05 |
ES |
269.40 |
11,031.83 |
2,887.71 |
3,392.10 |
SARIMA |
363.25 |
12,236.58 |
3,142.47 |
3,760.11 |
Best TS |
269.40 |
7,202.92 |
2,369.90 |
2,537.06 |
Comb AM |
305.91 |
8,747.67 |
2,597.31 |
2,791.28 |
Comb GM |
307.00 |
8,726.13 |
2,600.03 |
2,785.35 |
Comb HM |
308.09 |
8,704.59 |
2,603.14 |
2,779.32 |
Comb IMAPE |
291.19 |
8,552.77 |
2,578.36 |
2,752.84 |
Comb IMSE |
281.54 |
8,457.83 |
2,586.76 |
2,729.43 |
Comb IMAE |
291.68 |
8,551.19 |
2,578.12 |
2,752.49 |
Comb MV (r ¹ 0) |
281.67 |
8,458.58 |
2,586.95 |
2,729.46 |
Comb MV (r = 0) |
270.30 |
8,328.45 |
2,613.73 |
2,704.07 |
Comb LP min MAPE |
386.57 |
9,421.02 |
2,728.87 |
2,938.95 |
Comb LP min MSE |
383.23 |
9,167.81 |
2,668.34 |
2,883.02 |
Comb LP min MAE |
386.57 |
9,421.03 |
2,728.12 |
2,938.55 |
Comb MLRM1 |
381.68 |
9,356.10 |
2,649.40 |
2,923.85 |
Comb MLRM2 |
383.26 |
9,194.91 |
2,683.75 |
2,872.15 |
Comb FR |
327.38 |
9,072.20 |
2,615.92 |
2.870.27 |
Minimum |
269.40 |
7,202.92 |
2,369.90 |
2,537.06 |
Maximum |
386.57 |
12,236.58 |
3,268.12 |
3,760.11 |
Mean |
334.30 |
9,292.60 |
2,700.39 |
2,940.39 |
Standard-Deviation |
50.09 |
1,233.49 |
210.25 |
301.91 |
Individual (average performance) |
339.74 |
11,666.39 |
3,099.43 |
3,533.75 |
Combinations (average performance) |
333.99 |
8,905.97 |
2,633.88 |
2,834.58 |
Difference: individual versus combinations |
-1.69% |
-23.66% |
-15.02% |
-19.79% |
Source: Elaborated by the authors. Note: best mean, standard deviation, maximum
and minimum for the best TS (ES or SARIMA), according to the MAE criterion.
1. Graduate Program in Industrial & Systems Engineering (PPGEPS/UTFPR-PB). Federal Technological University of Paraná (UTFPR). Pato Branco Campus-PR. Email: donizetti@utfpr.edu.br
2. Graduate Program in Industrial & Systems Engineering (PPGEPS/UTFPR-PB). Federal Technological University of Paraná (UTFPR). Pato Branco Campus-PR. Email: gilson@utfpr.edu.br
3. Graduate Program in Industrial & Systems Engineering (PPGEPS/UTFPR-PB). Federal Technological University of Paraná (UTFPR). Pato Branco Campus-PR. Email: marcelo@utfpr.edu.br
4. Graduate Program in Industrial & Systems Engineering (PPGEPS/UTFPR-PB). Federal Technological University of Paraná (UTFPR). Pato Branco Campus-PR. Email: batistus@utfpr.edu.br
5. Regional Unit - Pato Branco. Sanitation Company of Paraná (SANEPAR). Pato Branco-PR. Email:bayerl_quimica@hotmail.com