HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 06) Año 2016. Pág. 1

Gráficos de controle de regressão para saúde utilizando Modelos Lineares Generalizados

Regression control charts using Generalized Linear Models

Cátia Michele TONDOLO 1; Mônica Cristina Bogoni SAVIAN 2; Leandro Cantorski da ROSA 3

Recibido: 10/10/15 • Aprobado: 22/11/2015

Contenido

1. Introdução

2. Metodologia

3. Procedimentos metodológicos

4. Resultados

5. Considerações finais

Referências

1. Introdução

O controle estatístico do processo (CEP) é um conjunto de ferramentas estatísticas utilizadas para aperfeiçoar a produção e adequar os processos às especificações (Joekes e Barbosa, 2013), garantindo assim a melhoria da qualidade (Teoh et al., 2014). No entanto, os gráficos de controle têm sofrido muitas modificações e melhoramentos sendo utilizados em diferentes áreas de atuação como na saúde. Algumas aplicações de CEP em saúde para controle de doenças e infecções podem ser vistas, por exemplo, em Woodall (2006), Burns et al (2005) e Benneyan, LLoyd e Plsek (2003).

Os gráficos de controle são recomendados para monitorar e melhorar o desempenho de um processo. As observações são plotadas, cronologicamente, como uma série de tempo e, os gráficos são construídos e analisados. Além disso, gráficos de controle utilizados de maneira adequada podem identificar sinais precoces de um possível surto ou epidemia (WOODALL, 2006).  

Gráficos de controle determinam estatisticamente uma faixa que é denominada de limites de controle, a qual é limitada pela linha superior (limite superior de controle, LSC) e uma linha inferior (limite inferior de controle, LIC), além de uma linha média, também chamada de linha central (LC). Esses limites de controle são definidos a partir dos dados coletados e da aplicação de técnicas estatísticas, e têm por objetivo verificar se o processo está sob controle, ou seja, sem a ação de causas especiais (MONTGOMERY, 2009). 

Suas funções são mostrar evidências do estado de controle estatístico e sinalizar a presença de causas especiais de variação. Um processo pode ser dito fora de controle por alterações na sua média ou na sua dispersão (variabilidade). Essas alterações podem ser consequências de causas especiais (como por exemplo, falha humana em um processo) ou causas comuns (como falha de um equipamento), gerando defeitos ou inconformidades em processos ou serviços (MACHADO, 2010).

No CEP, a variável ou característica de qualidade (CQ) é plotada em gráficos de controle tradicionais separadamente, sem levar em consideração a possível relação entre cada uma das variáveis, assumindo-se que as variáveis do processo são independentes e normalmente distribuídas. Segundo Montgomery (2009), quando existem vários parâmetros do processo e que podem ser monitorados simultaneamente, os gráficos de controle conhecidos como univariados não devem ser utilizados, pois, as várias CQ podem apresentar correlações entre si, o que prejudica o desempenho destes para sinalizar uma falta de controle do processo.

Uma maneira sugerida na literatura para a limitação relacionada a gráficos de controle tradicionais em monitorar situações em que são descritos por várias características, em vez de uma única característica de qualidade, é utilizar gráficos de controle de regressão, como os propostos por Haworth (1996), Ryan (1989) e por Mandel (1969).

O trabalho de Mandel (1969) apresentou o primeiro dos gráficos de controle de regressão e este utilizava os valores estimados do modelo de regressão para calcular os limites de controle. Haworth (1996) e Hawkins (1991), entre outros trabalhos, introdurizam os gráficos para regressão múltipla construídos com resíduos do modelo. Para modelar as CQ associadas ao processo e contornar o problema de não normalidade e assimetria de taxas ou proporções, por exemplo, Sant'Anna e Ten Caten (2010) modelam a fração de itens não conformes por meio de modelo de regressão beta.

Neste trabalho a característica a ser monitorada é o número de internações por doenças respiratórias em pessoas com 65 anos de idade ou mais. Para este tipo de dados de contagem, a distribuição Poisson é uma boa base para o ajuste, porém, quando a variância observada é maior do que as médias observadas, ocorre o fenômeno chamado de superdispersão, e nesse caso, o modelo Binomial Negativo é mais indicado, pois possibilita a modelagem da variância de modo mais adequado (PAULA, 2010).

Nelder e Wedderburn (1972) sugerem o uso de modelos lineares generalizados (MLG) como uma extensão dos modelos clássicos de regressão, sendo usados quando a variável resposta Y não é normalmente distribuída. Com isso serão utilizados os gráficos de controle de Shewhart para a média , gráfico de controle CUSUM (soma acumulada) e EWMA (médias movéis exponenciamente ponderandas) para monitorar os resíduos do modelo em situações em que os dados são não normais utilizando a metodologia de modelos lineares generalizados.

Desse modo pretende-se: i) Apresentar os modelos lineares generalizados; ii) Demonstrar o uso dos gráficos de controle Shewhart , CUSUM e EWMA para modelar os resíduos dos MLG's;  iii) Monitorar a variabilidade do número de internações por causas respiratórias na cidade de Brasília por meio de gráficos de controle.

2. Metodologia

2. 1 Modelos lineares generalizados

Os modelos normais lineares foram amplamente utilizados na tentativa de descrever a maioria dos fenômenos aleatórios. Mesmo quando o fenômeno sob estudo não apresentava uma resposta para a qual fosse razoável a suposição de normalidade, então Nelder e Wedderburn (1972), propuseram os modelos lineares generalizados (MLGs) que são uma extensão dos modelos normais lineares. A ideia básica destes modelos consiste em abrir o leque de opções para a distribuição da variável resposta, permitindo que a mesma pertença à família exponencial de distribuições.

Um MLG é construído a partir da decisão sobre a variável resposta e as variáveis explicativas e da escolha de uma função de ligação apropriada e uma distribuição de probabilidade da resposta. Algumas distribuições podem ser reunidas em uma família denominada família exponencial de distribuições, dentre elas estão a distribuição normal, binomial, Poisson, gama entre outras. Uma distribuição pertence à família exponencial de distribuições se sua densidade de probabilidade puder ser escrita da seguinte forma:

                                                                     (1)

em que  e  são funções conhecidas,  o parâmetro natural e  o parâmetro de dispersão.

Os MLG's são definidos pelas variáveis aleatórias independentes pertencentes à família exponencial de distribuições, pelo componente sistemático , e da função de ligação . Onde  é o preditor linear, , , é o vetor de parâmetros desconhecidos a serem estimados,  os valores das covariáveis ou variáveis explicativas e  a função de ligação monótona e diferenciável (CORDEIRO e DEMÉTRIO, 2007; PAULA, 2010). A escolha da função de ligação depende particularmente do problema e, pelo menos em teoria, cada observação pode ter uma ligação diferente. Alguns exemplos de função de ligação são potência, identidade, logarítmica, entre outras (PAULA, 2010). O método de estimação utilizado foi o de máxima verossimilhança que é um dos mais utilizados, pois possuem propriedades importantes como consistência e eficiência assintótica (BARROS, 2011; PAULA, 2010).

2.3 Gráfico de controle Shewhart

O gráfico de controle  é amplamente utilizado para monitorar a média. Este gráfico é um dos mais utilizados devido à simplicidade e facilidade de construção. Então se w é uma estatística que mede alguma característica de interesse de qualidade, e supondo que a média de w é  e o desvio padrão de w é , a linha central, o limite superior de controle, e o limite inferior de controle são dados por:

                                                                                                                  (2)

                                                                                                                    (3)

                                                                                                             (4)

onde k é a constante que define a largura dos limites (MONTGOMERY, 2009). Tradicionalmente, as linhas de controle ficam em uma distância de três erros padrão da linha central, originalmente sugerida por Shewhart (1931).

2.2 Gráfico de controle de CUSUM

O gráfico de controle CUSUM é considerado uma ferramenta indicada quando há interesse na detecção de pequenas e persistentes mudanças.Esse gráfico de controle é utilizado no monitoramento da média do processo. Incorpora a informação na sequência de valores da amostra, plotando as somas cumulativas dos desvios dos valores da amostra de um valor alvo. O CUSUM tabular acumula os desvios de µ0 que estão acima do valor alvo, com uma estatística C+, e acumulando desvios de µ0 que estão abaixo do valor alvo, com outra estatística C- (MONTGOMERY, 2009). Essas estatísticas C+ e C- são chamadas CUSUM's unilaterais superior e inferior, respectivamente. Calculam-se através das Equações 5 e 6:

                                                                       (5)

                                                                       (6)

onde os valores iniciais são ,  é o valor de tolerância ou folga e µ0 é o valor alvo.  é dado por:

                                                                                                                (7)

em que, µ1 é o valor da média fora de controle. E K é denominado de valor de referência, quanto menor o valor obtido, menor será a faixa de variação que o gráfico será capaz de detectar e aumentará a sensibilidade do gráfico.

2.3 Gráfico de controle EWMA

O gráfico de controle EWMA é geralmente escolhido quando se deseja detectar pequenos deslocamentos na média. Foram apresentados principalmente com o intuito de incorporar as limitações dos gráficos Shewhart. No gráfico EWMA o peso das observações decai à medida que ficam mais antigas.   é o fator utilizado para ponderação. Este gráfico é definido por (MONTGOMERY, 2009):

                                                                         (8)

em que,  é uma constante de amortecimento, x é a variável. Para o valor alvo utiliza-se .

Os limites de controle, considerando o período i = 1 são definidos pelas Equações 9, 10 e 11:

                                                                       (9)

                                                                                                                   (10)

                                                                      (11)

onde,  corresponde ao desvio padrão do processo quando em controle e L é a amplitude dos limites de controle.

3. Procedimentos metodológicos

Os dados referem-se ao número de internações hospitalares por causas respiratórias de pessoas com 65 anos ou mais do município de Brasília-DF, capital federal do Brasil e correspondem ao período de dezembro de 2007 a abril de 2015, totalizando 89 observações mensais. Estes foram retirados do TabNet (http://www2.datasus.gov.br/DATASUS/index.php) com fonte do Ministério da Saúde - Sistema de Informações Hospitalares do SUS (SIH/SUS).

As covariáveis utilizadas para o ajuste do modelo foram: velocidade do vento média (vvm em m/s), velocidade do vento máxima média (vvmm em m/s), evaporação piche (ep em mm), evaporação BH Potencial (EBHP em mm), evaporação BH Real (EBHR em mm), insolação total (it em kJ/m²), nebulosidade média (nm em décimos), precipitação total (pt em mm), número de dias de precipitação (ndp em mm), pressão média (pm), temperatura máxima média (tmaxm em ºC), temperatura compensada média (tcm em ºC), temperatura mínima média (tminm em ºC), umidade relativa média (urm em %), estas foram retiradas do site do Instituto Nacional de Meteorologia (INMET) através do BDMEP – Banco de Dados Meteorológicos para Ensino e Pesquisa (http://www.inmet.gov.br/projetos/rede/pesquisa/).

No caso, aos dados de contagem foi ajustado um MLG, utilizando o método backward onde é ajustado o modelo saturado, onde todas as covariáveis fazem parte do modelo e a partir desse modelo vai se retirando as covariáveis menos significativas do modelo. A cada passo do processo, uma nova variável era retirada do modelo. Para que uma variável permanecesse no modelo, era necessário que o seu coeficiente fosse significantemente diferente de zero (avaliado através do teste de Wald) e que o modelo com essa variável fosse significantemente melhor do que o modelo sem essa variável (avaliado através do teste F, com significância de 5%).

Para a avaliação da escolha do modelo foi feita a análise de diagnóstico através do pseudo R2 de Nagelkerke (1991), o qual é similar ao coeficiente de determinação obtido nos modelos lineares clássicos que mostra quanto o modelo explica da variação da variável resposta, e do critério de informação de Akaike (AIC) (Akaike, 1974). Foi feito também a análise de resíduos utilizando os resíduos componentes do desvio que são os mais utilizados em MLG (McCullagh e Nelder, 1989), que é capaz de detectar observações atípicas que influenciam o processo de ajuste do modelo e que serão utilizados na composição dos gráficos de controle. Analisado o envelope simulado e gráfico para a detecção de padrões ou de pontos discrepantes como alavancagem e distância de Cook.

A rotina de programação para ajuste do modelo foi implementada no software livre R (R Core Team, 2014). Para a confecção dos gráficos de controle utilizaram-se as funções disponíveis no pacote qcc (Quality Control Charts) (SCRUCCA, 2004).

4. Resultados

Primeiramente foi realizada uma análise descritiva a fim de observar o comportamento do número de internações, onde a média de internações foi de 1186 internações mensais, e apresentou um máximo e mínimo, respectivamente de 592 e 1950 casos e sua variância foi de 86167. Em seguida o ajuste dos dados, número de internações por doenças respiratórias, foi feito utilizando a distribuição de Poisson. Ajustado o modelo, construiu-se o gráfico de probabilidade normal com envelopes simulados dos resíduos deste modelo, que são construídos da mesma forma que para os modelos clássicos de regressão, usando-se, porém, a distribuição pertinente.

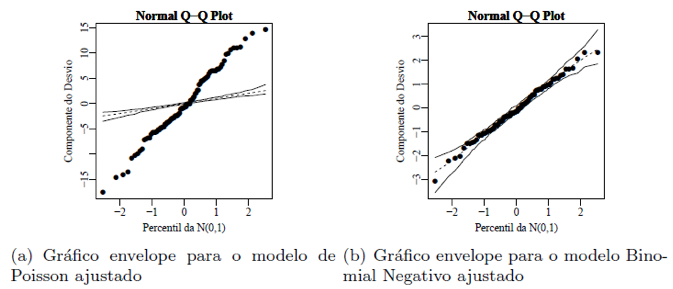
Figura 1 – Gráficos de envelopes simulados dos resíduos referentes
aos modelos de regressão para os  dados referentes ao número mensal
de internações hospitalares por doenças respiratórias.

Observa-se na Figura 1 (a) através do gráfico de envelope simulado dos resíduos que há fortes indícios que a distribuição de Poisson não é apropriada para os dados, pois se tem muitos pontos (resíduos) fora das bandas de confiança. Ainda, pode-se levar em consideração a ocorrência do fenômeno de sobredispersão já que os dados (resíduos) estão cruzando o envelope gerado que também pode ser justificado pelo valor do desvio D*(y; ) = 3436.65 (76 graus de liberdade) ser considerado alto. Já na Figura 2 (b), percebem-se indícios de um ajuste adequado, pois todos os pontos (resíduos) estão dentro ou sob as bandas de confiança do envelope gerado e que o valor do desvio é de D*(y; ) = 89,57 (81 graus de liberdade), esse foi o ajuste para o modelo de regressão binomial negativo que mostrou superioridade em relação ao modelo de regressão de Poisson.

Tabela 1 – Estimativas dos parâmetros referentes ao modelo de regressão binomial negativo ajustado.

Na Tabela 1 são apresentadas as estimativas de máxima verossimilhança para os coeficientes referentes ao modelo de regressão binomial negativo ajustado, bem como o erro padrão e o p-valor, com valor de AIC igual a 1228.5, sendo este o menor valor encontrado entre todos os modelos testados. As variáveis significativas, presentes no modelo são vvm, ebhp, it, ndp, tmaxm, tcm e tmnm.

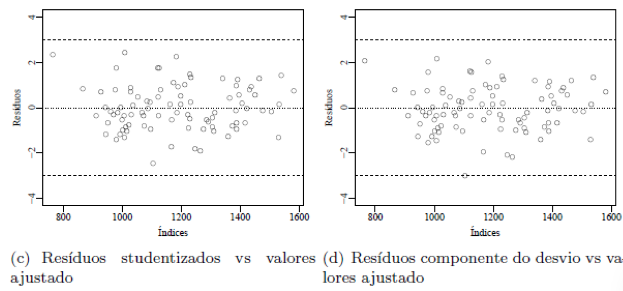
Figura 2 – Gráficos de resíduos para o modelo de regressão binomial negativa.    

Os gráficos de resíduos studentizados (ts) versus o valor ajustado e resíduo componente do desvio (td) versus o valor ajustado para o modelo de regressão binomial negativo são apresentados nas Figuras 2 (c) e 2 (d), respectivamente. Através desses gráficos é possível identificar  o bom ajuste, sendo que nos dois gráficos os pontos estão concentrados em torno de zero, com algumas variações que não excedem os limites. Então observa-se que praticamente todos os resíduos estão dentro do intervalo de -3 à 3, que é o esperado em um bom ajuste.

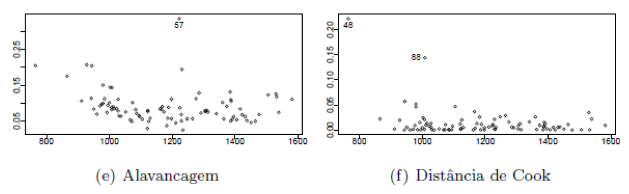
Figura 3 – Gráficos de análise de  diagnóstico para a verificação de pontos de alavanca (e) e para a verificação de pontos de influência (f).     

Na Figura 3 são apresentados os gráficos de análise de diagnóstico do modelo selecionado. A Figura 3 (e) apresenta o gráfico de alavancagem do modelo de regressão binomial negativo, que segundo Oliveira (2013), mede a influência das respostas sobre o valor ajustado, ou seja,  mede a distância entre a variável Yi e as observações no espaço definido pelas variáveis explicativas. Esses valores são considerados atípicos se estiverem próximos de 1, neste caso pode-se observar que a observação 57 foi identificada, porém não pode ser considerada um ponto de alavanca, pois não pode ser considerado perto de 1.

A Figura 3 (f) apresenta o gráfico da distância de Cook, neste caso observam-se se existem os pontos influentes em , quanto mais próximos de 1 esses pontos estiverem, mais influentes serão. As observações 48 e 88 foram identificadas e estão mais próximas de 1 que as demais, porém não podem ser consideradas influentes em  e ao serem retirados do modelo não modificam significativamente as estimativas do modelo.

Para a confecção dos gráficos de controle foram utilizados os resíduos componentes do desvio e são dados a seguir:

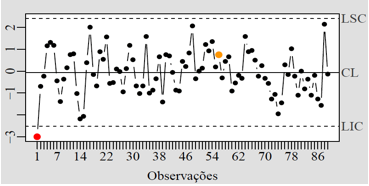
Figura 4 – Gráfico  para os resíduos médios do modelo de regressão log linear binomial negativo.

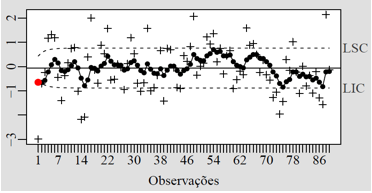
Figura 5 – Gráfico EWMA para os resíduos médios do modelo de regressão log linear binomial negativo.

A Figura 4 apresenta o gráfico de controle Shewhart  que não foi efetivo para detectar as mudanças ocorridas nos dados, pois os gráficos de Shewhart apesar de simples e de fácil interpretação são mais apropriados para detectar grandes mudanças na média do processo. A Figura 5 apresenta o gráfico de controle EWMA que também não foi sensível às pequenas mudanças do número de internações considerando quase todas as observações como em controle.

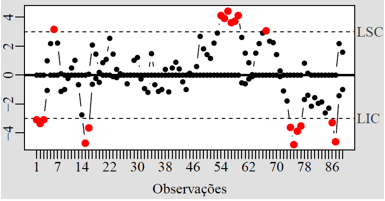
Figura 6 – Gráfico CUSUM para os resíduos do modelo de regressão binomial negativo.

A Figura 6 apresenta o gráfico CUSUM para os resíduos componentes do desvio do modelo de regressão log linear binomial negativo, podem-se observar a partir deste gráfico alguns pontos fora dos limites de controle, esses pontos foram identificados e compreendem aos meses do ano em que houve um número muito baixo ou muito alto de internações hospitalares por doenças respiratórias. Nos meses compreendidos no período do verão o número de internações tende a ser mais baixo devido ao aumento da temperatura, enquanto que nos meses que compreendem o inverno este número tende a aumentar, devido às baixas temperaturas, que neste caso é o fator que mais influencia no aparecimeto de doenças do apararelho respiratório, bem como a influência de outros fatores como, por exemplo, a velocidade do vento média, a evaporação, a insolação total e o número de dias de precipitação. Assim, o gráfico faz a previsão antes do real fora de controle, antes dos meses em que as internações aumentaram, sendo um bom índicio para intervenções de saúde na população.

5. Considerações finais

Este trabalho teve a finalidade de monitorar o número de internações hospitalares por causas respiratórias de pessoas com 65 anos ou mais na cidade de Brasília-DF no período de dezembro de 2007 a abril de 2015 utilizando gráficos de controle. Ao considerar-se o uso de modelos lineares generalizados, foi possível propor um modelo para o ajuste do número de internações por causas respiratórias e através dos resíduos componentes do desvio deste modelo utilizar as técnicas de controle estatístico de processo, como os gráficos , CUSUM e EWMA.

Os resultados demonstraram que o gráfico de controle CUSUM mostrou-se muito eficiente na detecção de "falta de controle" no caso do número de internações por causas respiratórias. Pelas suas características, onde as probabilidades têm relação com o período anterior, ou seja, por exemplo, o mês de fevereiro depende do mês de janeiro, ou seja, foi mais sensível as mudanças no comportamento.

De acordo com a análise realizada, é interessante dar prosseguimento ao monitoramento através de gráficos de controle para verificar o comportamento do número de internações hospitalares e investigar os motivos que levam ao aumento quando este é sinalizado. Utilizar os resultados como plano de ação, para sugerir campanhas como propagandas veiculadas por meios de comunicação para incentivar a população, nas épocas em que o número de internações cresce, a tomar medidas preventivas e verificar posteriormente os benefícios.

Referências

AKAIKE, H. (1974); A new look at the statistical model identification. IEEE Transactions on Automatic Control, v.19, n.6, p.716-723.

BARROS, F. U. (2011); Matriz de covariâncias do estimador de máxima verossimilhança corrigido pelo viés em modelos lineares generalizados com parâmetro de dispersão desconhecido. Dissertação de Mestrado, Universidade Federal de Campina Grande – UFCG.

BENNEYAN, J. C.; LLOYD, R. C.; PLSEK, P. E. (2003); Statistical process control as a tool for research and healthcare improvement. Quality and Safety in Health Care, v. 12, n. 6, p. 458-464.

BURNS, C. M.; BENNETT, C.J.; MYERS, C.T.; WARD, M. (2005); The use of CUSUM analysis in the early detection and management of hospital bed occupancy crises. The Medical Journal of Australia, v. 183, n.6, p. 291-294.

CORDEIRO, G. M., DEMÉTRIO, C. G. B. (2007); Modelos lineares generalizados. In: Minicurso para o 12° SEAGRO e a 52° Reunião Anual da RBRAS. UFSM, Santa Maria, RS, Julho.

HAWKINS, D. M. (1991); Multivariate quality control based on regression-adjusted variables. Technometrics 33 (1), 61-75.

HAWORTH, D. A. (1996); Regression control chart to manage software maintenance. Journal of Software Maintenance, 8 (1), 35-48.

JOEKES, S., BARBOSA, E. P. (2013); An improved attribute control chart for monitoring non-conforming proportion in high quality processes. Control Engineering Practice. 21, 407-412.

MACHADO, J. F. (2010); Método Estatístico: Gestão de Qualidade para Melhoria Continua. São Paulo: Saraiva.

MANDEL, B. J. (1969); The regression control chart. Journal of Quality Technology. 1 (1), 1-9.

McCULLAGH, P., NELDER, J. A. (1989); Generalized linear models. London/New York. Chapman and Hall.

MONTGOMERY, D. C. (2009); Introdução ao Controle Estatístico da Qualidade. Editora LTC.

NAGELKERKE, N. J. D., (1991); A note on a general definition of the coeficient of determination.

Biometrika 78 (3), 691-692.

NELDER, J., WEDDERBURN, R. W. M. (1972); Generalized linear models. Journal of the Royal Statistical Society, 135 (3), 370-384.

PAULA, G. A. (2010); Modelos de Regressão com apoio computacional. Instituto de Matemática de São Paulo - Universidade de São Paulo.

R CORE TEAM. (2014); R: A language and environment for  statistical computing. R Foundation for Statistical Computing,   Vienna, Austria.

RYAN, T. P. (1989); Statistical Methods for Quality Improvement. John Wiley & Sons, New York, NY, 446 pp.

SANT'ANNA, A. M. O., Ten CATEN, C. S. (2010); Modelagem de fração de não conformes em processos industriais. Pesquisa Operacional 30 (1), 53-72.

SCRUCCA, L. (2004) qcc: an R package for quality control charting and statistical process control. R News, p. 11-17.

SHEWHART, W. (1931); Economic control of quality of manufactured product. New York: D. Van Nostrand Company, 501 p.

TEOH, W., KHOO, M. B., CASTAGLIOLA, P., CHAKRABORTI, S. (2014); Optimal design of the double sampling chart with estimated parameters based on median run length. Computers & Industrial Engineering, 67, 104-115.

WOODALL, W. H. (2006); The use of control charts in health-care and public-health surveillance. Journal of Quality Technology, 38.2, 89-104.

YU, J.; LIU, J. (2011); LRProb control chart based on logistic regression for monitoring mean shifts of auto-correlated manufacturing processes. International Journal of Production Research, v. 49, n. 8, p. 2301–2326.

1.Programa de Pós-Graduação em Engenharia de Produção- PPGEP. Universidade Federal de Santa Maria – UFSM – Santa Maria/RS – Brasil. Email: cacamt@gmail.com
2 Programa de Pós-Graduação em Engenharia de Produção- PPGEP. Universidade Federal de Santa Maria – UFSM – Santa Maria/RS – Brasil. Email: monicabogoni@yahoo.com.br
3. Programa de Pós-Graduação em Engenharia de Produção- PPGEP. Universidade Federal de Santa Maria – UFSM – Santa Maria/RS – Brasil. Email: leski78@hotmail.com