 HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN
HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN Espacios. Vol. 37 (Nº 05) Año 2016. Pág. 15
Vanusa Andrea CASARIN 1; Adriano Mendonça SOUZA 2; Ronaldo Leão de MIRANDA 3; Marcelo Borges FRANCO 4; Antônio Vanderlei dos SANTOS 5
Recibido: 09/10/15 • Aprobado: 10/11/2015
ABSTRACT: The use of plants with therapeutic effects among peoples is one of the oldest practices employed for the treatment of human diseases. Thus, the present study aimed to investigate the medicinal plants cultivated and used in the community Corner of the plate, municipality of Inhuma-PI. For this semi-structured interviews were applied to the 45 residents of the locality in order to collect information on socio-economic aspects and of traditional local Botanical knowledge. 43 species were identified belonging to 25 botanical families. The most used were the leaves, cited by respondents 58.30, followed by seed with 15.30 citations of use and fruit with 10.60. The categories of diseases established by the who, the who held off the greatest number of species were the "general symptoms and signs" with 27 species cited, followed by "digestive" with 23 species. You can tell that this is a community of simple habits with a relatively small population that cultivates some old ways including the use of plants to cure their ills. It is understandable that meet the local use of species as well as the knowledge about historically this use, it is of the utmost importance for preservation of local culture and diversity of flora. |
RESUMO: A utilização de plantas com efeitos terapêuticos entre os povos é uma das mais antigas práticas empregadas para tratamento de enfermidades humanas. Assim, o presente trabalho objetivou investigar as plantas medicinais cultivadas e utilizadas na comunidade Recanto do prato, município de Inhuma/PI. Para isso foram aplicadas entrevistas semiestruturadas aos moradores 45 da localidade a fim de coletar informações sobre aspectos socioeconômicos e de conhecimento botânico tradicional local. Foram identificadas 43 espécies pertencentes a 25 famílias botânicas. As partes mais utilizadas foram as folhas, citadas por 58,30% dos entrevistados, seguidos de semente com 15,30% citações de uso e fruto com 10,60%. Das categorias de doenças estabelecidas pela OMS, as que detiveram maior número de espécies agrupadas foram a de "sintomas e sinais gerais" com 27 espécies citadas, seguida de "doenças do aparelho digestivo" com 23 espécies. Percebe-se que se trata de uma comunidade de hábitos simples com uma população relativamente pequena que cultiva alguns costumes antigos entre eles o uso de plantas para cura de seus males. Compreende-se que conhecer o uso local de espécies bem como o conhecimento que cerca historicamente esse uso, é de suma importância para preservação da cultura local e diversidade da flora. |
Statistical Process Control (SPC) is a strategy for quality improvement, and it uses techniques by which it is possible to detect a defective item after the product being processed. When deviations from the target are not possible for several reasons or not permitted during the production, one possibility to avoid defective products is to interfere with the system and try to adjusting it so that obtaining a product with quality. This kind of procedure is denominated feedback control.
The feedback control is a part of Engineering Process Control (EPC), which uses measurements to prescribe changes in the intended process to bring the final output process to its desired target, where the variable's future values are used to re-feed the system Sachs & Ingolfsson (1995).
Thus, the forecasting methods are used to determine, beforehand, when this problem may occur. On the contrary of SPC, the EPC does not try to eliminate the identified causes, but it applies compensations to the system through continuous adjustments to maintain the output variables as close as possible to the desired target MaC Gregor & Harris (1990), (Montgomery et al,1994), Souza (2000). However, both methodologies, SPC and EPC, have the same purpose of avoiding defective items and reducing the variability.
The main purpose of this research is to make a feedback adjustment in a productive process in presence of volatility by analyzing the mean and volatility behavior in combination based on their forecasted values. Thus, in order to reach a final product within the specifications, a control equation was developed using parameters found through the proposed methodology Box & Luceño (2004).
The link between SPC and EPC is an important way to show how to manage disturbances in cases where they cannot be removed (Souza et al, 2004ab), the method is used in order to reach the proportional-integral controller, considering linear and non-linear models to forecast the process.
This paper is organized in five sections: section 1 of methodological aspects, section 2 of results presentation and section 3 the concluding remarks.
According to Box & Luceño (2004), Box & Luceño (1997), the feedback adjustment is appropriate when no control has been applied and the instabilities occur because of natural raw-materials (oil, wood, wool), non-controlled environmental variables (room temperature, humidity) and several other reasons.
If the special causes that generate instability in the system cannot be eliminated, a procedure for adjusting variables through compensatory actions should be used in order to maintain the process as close as possible to the specified target Box (1991), Box & Kramer (1992), Hoerl & Palm (1992), MaCGregor (1992), Franklin et al. (1994), Box et al. (1994).
This methodology proposed is useful because many industrial processes show disturbances that cannot be removed, therefore they need to be compensated and it considers the level and the volatility system.
To reach the main purpose of this research and considering that the data is auto-correlated, it is necessary to follow the methodological steps:
STEP 1: To provide a descriptive statistics in order to investigate the variable behavior regarding the stationary and test the Granger causality direction Granger (1969).
STEP 2: To determine a linear model using the least squares (LS) estimation method Gujarati (2000) as a way to get residual ut ≈ N(0, σ2), which is the white noise. This step is necessary to reveal the relationship among the variables and know its forecasted values, as in equation (1).
![]()
STEP 3: After estimating the linear model, residuals are investigated to detect the presence of autoregressive conditional heteroscedasticity (ARCH) by the ARCH-LM test proposed by Campos (2007). Thus, we can observe if the residual series has zero mean and if it is non auto correlated according to Bollerslev (1992). However, if the quadratic residual series is correlated, the residual series is denominated heteroscedasticity and a non linear model should be used to represent and the series has a non-pure random behavior.
STEP 4: If the residual has heteroscedasticity a linear and non-linear modeling - the combined modeling - is estimated by linear and non-linear models considering the level and volatility effects of the series, which is simultaneously estimated. In this way, the auto correlation is eliminated in level and in the variability, producing an accurate estimative Bollerslev (1992).
An ARCH (m) model, where m denotes the model order, expresses the conditional variance model for the conditional mean as a quadratic function of past innovations (SILVA et al, 2005).
To ensure that the conditional variance is positive and weakly stationary, the following parametric restrictions are necessary: for all t = 2, …,m and ![]() .
.
STEP 5: The process is investigated by applying the X-bar control charts for individual measures in the residuals free of autocorrelation and heteroscedasticity effects (Montgomery et al, 1994), Del Castillo (2002) and if the process shows any kind of instability and it is not possible to identify, the feedback corrective measures can be quantified to be carried out in the future.
STEP 6: To apply the corrective action to maintain the process under control, the feedback equation follows Box & Luceño (2004), (Souza et al, 2004) will be used. The deviances in the process are represented by , in which is the variable being analyzed and T is the value to be reached by this variable. The feedback corrective measures can be quantified to be carried out in the future, following the methodology of proportional-integral controller (PIC) described in Box & Luceño (1997), Box (1991).
And according to Box (1991), (Souza et al, 2004), the discrete proportional-integral control is achieved by using (2).

where, xt provides the level of adjustment that should be compensated in the process. The symbol g is called system gain or impact, and it has the same function of the regression coefficient and could be determined by the machine manual or by the engineering at the plant; et is the disturbance forecast error created by the difference between the real values forecasted minus the target. This series is forecasted to know about its behavior in the future.
Using the relationship showed in Box & Luceño (2004), it is observed that the process has inertia and it would be more reasonable to suppose that not only the adjustment but the previous adjustments might be taken into account. A reasonable supposition is that the past adjustments should be discounted exponentially using the exponentially weighted moving average (EWMA) statistic to find the smooth constant and θ = 1 – λ.
Data are gathered at equidistant periods and the adjustments related to the disturbance of each variable are carried out at equidistant periods. Hence, a system of discrete adjustment in relation to the variable disturbances is considered. Equation (2) provides the level of adjustment that should be compensated in the process.
The regression analysis shows the delay found in the system. Each shift noticed and the input in the system may be accomplished in one-hour interval since data were read every hour (SOUZA, 2000).
STEP 7: To interpret the system adjustment controller. For such, it is necessary to identify the variables to be adjusted and then to find the target (T) values. The purpose is to maintain the process as close as possible to this T value. This process is performed by manipulating the input variables.
Equation (7) informs the level of control to be introduced in the process. Since the control process in this study is carried out by regulating a dial knob on the control panel, a positive (+) numerical result obtained from the equation indicates that the regulating dial should be turned clockwise, so that a greater amount of heat is released. Likewise, a negative (-) numerical result obtained indicates that the regulating dial should be turned counterclockwise, so that less heat is released into the oven (SOUZA, 2000).
This methodology is exemplified by a practical application in a carbonated beverage company. Data were gathered from the pre-form blow molding machine and variables identified as the most pertinent ones involved in the productive process include oven heating temperature (OHT), heating percentage adjustments (HPA). These variables are fundamental mainly for the good performance of blow molding machines especially for the resin transformation (polyethylene terephalate - PET) derived from petroleum into a 2-liter plastic bottle.
The temperature in the ovens should vary between 140 ºC and 154 ºC, and the pre-forms should remain inside the oven for 48 seconds. The series has 202 observations for each variable taken at one-hour intervals in three daytime shifts at the blow molding machine.
As preliminary analysis, it was necessary to investigate the time series stationary. The tests used were the Augmented Dickey-Fuller (1984) - (ADF), Phillips and Peron (1988) - (PP) and test Kwiatkowski-Phillips-Schmidt-Shin (1992) - (KPSS) Enders (1995), Maddala (1992).
The variable OHT shows non-stationary in level, but in the first difference it is stationary. As the null hypothesis of ADF and KPSS tests are distinct, it is expected that the two tests point out the same decision about the series stationary. The variable HPA is stationary in level and in differences as stated by all testes.
The test used to check for causality direction was The Granger causality test Granger (1969), and the variables involved in this test are the series in levels of OHT and HPA. The test shows that the variable OHT causes the HPA and the HPA causes the OHT. Therefore, the causality is bi-directional, shows a situation where the feedback equation is recommended to be applied to maintain the process under control.
The variability of the process was investigated by R and X-bar chart applied in the residual series obtained from the combined linear and non-linear model in Table 3. Even if R and charts are revised, the residue process still presents instability according to Box (1991), Montgomery (1997), Conover (1999). Since the engineers at the plant could not detect any special cause for these points to be out of control, compensation in the system is recommended.
3.1 Modeling the variables to determine the forecast values
In order to achieve feedback control, the variables are modeled in terms of level and variability through multiple linear regression analysis and ARCH models. This methodology reveals the relationship among the variables and their future values. The regression analysis is carried out to determine the disturbance forecasts as shown by Gujarati (2000), Souza et al. 2004ab, Enders (1995), Maddala (1992), Conover (1999), Intriligator et al (1996), Hill et al. (1999). The variability is modeled according to Baillie & Chung (1996), Bollerslev (1986), Costa & Baidya (2001), Sadorsky (1999) using the ARCH family modeling, shown in Table 1.
TABLE 1
MODELING OF VARIABLES OHT AND HPA IN THE OVEN TEMPERATURE
Mean equation |
||||
OHT |
Coefficient |
Std. Error |
z-Statistic |
Prob. |
OHT(-1) |
0.595870 |
0.057820 |
10.30554 |
0.0000 |
Δ(HPA(-1) |
0.676604 |
0.296587 |
2.281297 |
0.0225 |
Variance conditional equation |
||||
α0 |
7.495263 |
0.861055 |
8.704738 |
0.0000 |
|
0.423541 |
0.105656 |
4.008663 |
0.0001 |
Model Adjustment Statistics |
||||
R-squared |
0.249851 |
Mean dependent var |
147.7870 |
|
Adjusted R-squared |
0.242235 |
S.D. dependent var |
4.034740 |
|
S.E. of regression |
3.512228 |
Akaike info criterion |
5.261347 |
|
Sum squared resid |
2430.142 |
Schwarz criterion |
5.343805 |
|
Log likelihood |
-521.1347 |
Hannan-Quinn criter |
5.294717 |
|
Durbin-Watson stat |
2.435421 |
|
||
Note: Δ = variable in the first differences; the dependent variable was
OHT and the estimation method was ML – ARCH Marquardt method, using normal distribution.
To confirm the absence of conditional heteroscedasticity in the residuals of the estimated model, the Lagrange multiplier test proposed by Engle (1982) was applied to the final models, where we observed that residuals were non-heteroscedastic. This was confirmed by the Durbin-Watson test whose null hypothesis postulates no autocorrelation showing that the residuals can be considered independent, since all the series of major components had values close to 2.0 (ENDERS,1995).
All the parameters estimated are significant and reveal a characteristic white noise. Considering that the variance is not constant overtime Costa & Baidya (2001), it has shown that if these characteristics are neglected, there are consequences in terms of the quality of the parameter estimates and consequently in the forecasting values and residuals. Thus, non linear models must be used to capture these effects. Figure 1 shows the conditional variance behavior.
Figura 1. Conditional variance of the residual from the joint linear and non-linear model
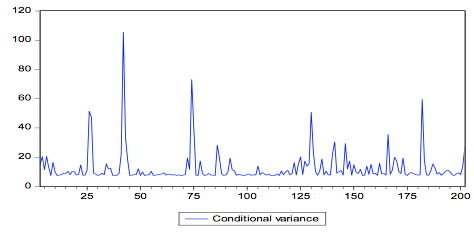
Figure 1 shows that around the observations 25, 45, 75, 130 and 185 there are peaks of volatility, but around the period 45 it is the strongest. It is important to notice that at the end of the period, the volatility is decreasing, and the residuals become each time less heteroscedastic. The important fact here is that implementing a feedback action with low volatility, the change may be smooth.
In order to help to maintain the variability in the stable system and to evaluate the impact that a change of a unit in the independent variable causes in the dependent variable, the feedback control methodology is useful. The variability in the system, which is represented by equal to 0.423541, shows that an external shock in the system takes a short time to make the volatility return to its usual level. Thus, the system must be monitored after each adjustment that was made in the process.
According to the company engineers and through the tests performed at the machine, the best value of g is 1.3. The adjustment knob has a scale of 1 to 100, where the change in 10 units of the adjustment percentage causes a change of one unit in the heating percentage. The proportion is thus from one centesimal to one decimal. In other words, a one-point change to the adjustment knob numerical scale causes a 0.1 change in percentage points of the heating percentage variable.
The adjustment percentage provides greater or lesser heat release, affecting the oven temperature, which heats the pre-form for blowing. A common practice among all machine operators is to reach the correct adjustment of the oven temperature by turning the adjustment percentage knob until the ideal temperature is achieved. In these attempts many pre-forms are rejected, generating a high number of rejects. Table 2 presents error values for the last four values of the sample.
TABLE 2
ERROR VALUES FOR OVEN TEMPERATURE
Sample |
Real Value |
Forecasted Value |
Error |
199 |
150.5 |
147.6401103 |
2.859889719 |
200 |
145.5 |
147.6434236 |
-2.143423621 |
201 |
137.6 |
145.7509081 |
-8.150908109 |
202 |
145.6 |
146.5177054 |
-0.917705414 |
In the stage of applying the controller, the main task is to determine the variable behavior so that the adjustments made can maintain the process as close as to the target value as possible. The variability of the process is not verified again because it was already done in a previous stage Box et al (1994), Robinson & Hu (1968).
In this paper, deviations from the target are expressed by the difference between the values read by the operator from the machine panel, considering the oven temperature at the current instant and the established target value. For weighing the disturbances, the smooth constant is used. This procedure minimizes the sum square errors found using the EWMA Lucas & Saccucci (1990), Crowder (1987), Montgomery & Mastrangelo (1991). The best constant to be used in the feedback equation was determined through the minimum least square errors and the search ranged from 0.1 to 0.99 incremented by 0.01. The best chosen values for and θ were 0.46 and 0.54, respectively.
Once the values of g and are known, the adjustments for the last three gathered values are applied to the proportional integral equation 2:
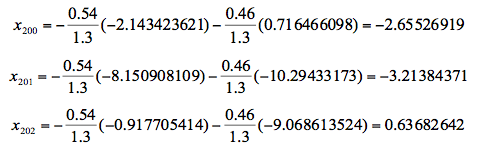
Since the temperature control knob has a numerical scale for the period 200, it is possible to introduce an adjustment by turning the knob counter clockwise approximately -2.65 units; for the period 201, turning the control knob counter clockwise approximately 3.21 units; and turning the knob clockwise 0.63 units for the period 292.
With the controller proposed and implemented, the machine operator can anticipate the adjustment value to be made to the blow molding machine in a clear and understanding manner. To accomplish that, the company must provide some training to its operators and should also continue to monitor the variables that are part of the process.
The purpose of the entire project is to save the company resources by avoiding the waste of pre-forms with additional work and re-inspection. Considerable amount of raw material was being discarded and sold as scrap for a low value when compared to that of the original product.
We must notice that during the period of analysis there were some facts that might have contributed to the process instability, such as mechanical problems of the blow molding machine, opening the chimney, opening the exhaust engine, room temperature, burnt oven lamp, lack of records taken by the machine operator, carelessness in writing down the values, constant change of raw materials, lack of consistent procedures for operating the machine and operator training.
The controller allows the system feedback so that the variables that are off their specified targets can be continually adjusted, which leads to increasing process control considering not just the series level to evaluate the adjustment but also the volatility behavior.
The use of SPC and EPC applied in data that presents heavy tail, which in most of cases signalize the volatility presence, shows that it must be considered not only to give better parameters and consequently more accurate errors, but to make possible to understand the variable persistence, what is the time that the series will take to return to its normal level during the process.
These two methodologies where of great value to evaluate the productive processes, the variable was also forecasted using the dynamic regression, which through its residues enables to incorporate the volatility behavior in the control equation.
BAILLIE, R.; CHUNG, C.F. (1996); Analyzing inflation by the fractionally integrated ARFIMA-GARCH model. Journal of Applied Econometrics, vol. 11, pp. 23-40.
BOLLERSLEV, T. (1986); Generalized autoregressive conditional heteroscedasticity. Journal of Econometrics, vol. 31, pp. 307-327.
BOLLERSLEV, T.; CHOU, R.Y.; KRONER, R.Y. (1992). ARCH modeling in finance: A review of the theory and empirical evidence. Journal of econometrics, vol. 52, n. 1-2, pp. 5-59.
BOX, G.E.P. (1991); Feedback control by manual adjustment. Quality Engineering, v. 4, n. 1, pp. 143-151.
BOX, G.E.P.; JENKINS, G.M.; REINSEL, G.C. (1994); Times series analysis: forecasting and control, 3. ed., Prentice Hall Inc., Englewood Cliffs, NJ.
BOX, G.E.P.; KRAMER, T. (1992); Statistical process monitoring a feedback adjustment - A discussion. Technometrics, August, v. 34, pp. 251-285.
BOX, G.E.P.; LUCEÑO, A. (1997); Statistical control by monitoring and feedback adjustment, John Wiley & Sons, Inc. NY.
BOX, G.E.P.; LUCEÑO, A. (2004); Discrete proportional-integral adjustment and statistical process control. Journal of Quality Technology, July, v. 29, n. 3, pp. 248-260.
CAMPOS, K.C. (2007); Análise da volatilidade de preços de produtos agropecuários no Brasil. Revista de Economia de Agronegócio, v. 5, n. 3, pp. 303-328.
CONOVER, W.J. (1999); Practical Nonparametric statistics. 3. ed., John Wiley and Sons, Inc.
COSTA, P.H.S.; BAIDYA, T.K.N. (2001); Propriedades estatísticas das séries de retornos das principais ações brasileiras. Pesquisa Operacional, v. 21, n. 1, pp. 61-87.
CROWDER, S.V. (1987); A simple method for studying run-length distributions of exponentially weighted moving average charts. Technometrics, November, v. 29, n. 4, pp. 401-407.
DEL CASTILLO, E. (2002); Statistical Process Adjustment for Quality Control, Wiley series in probability and Statistics, John Wiley and Sons, Inc., New York.
ENDERS, W. (1995); Applied econometric time series. Wiley series in probability and mathematical statistics. John Wiley and Sons, Inc., New York.
ENGLE, R.F. (1982); Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometria, v. 50, n. 4, pp. 987-1008.
FRANKLIN, F.G.; POWELL, D.J.; EMAMI-NAEINI, A. (1994); Feedback control of dynamic systems, 3. ed., Addison-Wesley Publishing Company, Inc. New York.
Granger, C.W.J. (1969); Investigating causal relations by econometric models and cross-spectral models. Econometrica, v. 34, pp. 541-551.
GUJARATI, D.N. (2000); Econometria básica, São Paulo: Makron Books.
HILL, C.; GRIFFITHS, W.; JUDGE, G. (1999); Econometria. São Paulo: Saraiva.
HOERL, R.W.; PALM, A.C. (1992); Integrating SPC and APC – Discussion. Technometrics, August, v. 34:, pp. 268-272.
INTRILIGATOR, M.D.; BODKIN, R.G.; HSIAO, C. (1996); Econometrics models, techniques and applications. Upper Saddle River: Prentice Hall.
LUCAS, M.J.; SACCUCCI. M.S (1990). Exponentially-Weighted Moving Average Control Schemes: Properties and Enhancements. Technometrics, February, v. 32, n. 1, pp. 1-12.
MACGREGOR, J.F. (1992); Integrating SPC and APC - A discussion. Technometrics, August, v. 34, n. 3, pp. 273-275.
MACGREGOR, J.F.; HARRIS, T.J. (1990); Discussion of EWMA Control Schemes: Properties and Enhancement. Technometrics, v. 32, pp. 23-26.
MADDALA, G.S. (1992); Introduction to econometrics. 2.ed., Englewood Cliffs: Prentice Hall.
MONTGOMERY, D.C. (1997); Introduction to statistical quality control. 3 ed., New York: John Wiley & Sons, Inc.
MONTGOMERY, D.C.; KEATS, J.B.; RUNGER, G.C.; MESSINA, W.S. (1994); Integrating statistical process control and engineering process control. Journal of Quality Technology, April, v. 26, n.2, pp.79-87.
MONTGOMERY, D.C.; MASTRANGELO, C.M. (1991); Some statistical process control methods for autocorrelated data. Journal of Quality Technology, July, 23, pp. 179-204.
ROBINSON, P.B.; HU, T.Y. (1978); Average runs lengths of geometric moving average charts by numerical methods. Technometrics, February, v. 37, n. 1.
SACHS, E.; HU, A.; INGOLFSSON, A. (1995); Run by run process control: combining SPC and feedback control. IEEE Transactions on semiconductor manufacturing, February, v. 8, n. 1, pp. 26-43.
SADORSKY, P. (1999); Oil price shocks and stock market activity, Schulich School of Business, York University. Energy Economics, v. 21, pp. 449-469.
SILVA, W.S.; SÁFADI, T.; CASTRO JÚNIOR, L.G. (2005); Uma análise empírica da volatilidade do retorno de commodities agrícolas utilizando modelos ARCH: os casos do café e da soja. Revista de Economia e Sociologia Rural, v. 43, n. 1, pp. 120-134.
SOUZA, A.M. (2000); Monitoração e ajuste de realimentação em processos produtivos multivariados, Florianópolis: UFSC, 2000, 166p. Tese (Doutorado em Engenharia de Produção) - Universidade Federal de Santa Catarina.
SOUZA, A.M.; SAMOHYL, R.W.; MALAVÉ, C.O. (2004a); Multivariate feedback control: an application in a productive process. Computers & Industrial Engineering, v. 46, p. 837-850.
SOUZA, A. M.; SAMOHYL, R. W.; MALAVÉ, C. O. (2004b); Aplicação de um modelo paramétrico multivariado para o controle da temperatura de fornos de túnel. Revista Produção, v. 14, n. 2, p. 82-94.
1. Universidade Regional Integrada do Alto Uruguai e das Missões, PPGGEO. Santo Ângelo, RS, Brasil– vanusa.casarin@gmail.com
2. Universidade Federal de Santa Maria, CCNE. Santa Maria, RS, Brasil– amsouza.sm@gmail.com
3. Universidade Regional Integrada do Alto Uruguai e das Missões, Administração. Santo Ângelo, RS, Brasil– ronaldo_leaomiranda@hotmail.com
4. Instituto Federal Farroupilha, Gestão de Pessoas. Santa Rosa, RS, Brasil. – marceloborgesfranco@gmail.com
5. Universidade Regional Integrada do Alto Uruguai e das Missões, PPGGEO. Santo Ângelo, RS, Brasil– vandão@santoangelo.uri.br