![]() Espacios. Vol. 36 (Nº 12) Año 2015. Pág. E-1
Espacios. Vol. 36 (Nº 12) Año 2015. Pág. E-1
Geometria Hiperbólica: possibilidades para o ensino do conhecimento geométrico não euclidiano
Hyperbolic Geometry: possibilities for teaching geometric knowledge non-Euclidean
Mariany Layne de SOUZA 1; Simone LUCCAS 2
Recibido: 03/03/2015 • Aprobado: 24/05/2015
Contenido
- 2. O Quinto postulado e o surgimento das Geometrias Não Euclidianas
- 3. Geometria Hiperbólica
- 4. O uso do software NonEuclid como recurso ao ensino da Geometria Hiperbólica
- 5. Procedimentos Metodológicos
- 6. Análise dos Resultados
- 7. Considerações finais
- Referências
RESUMO: Este artigo aborda uma pesquisa realizada no âmbito do ensino das Geometrias Não Euclidianas, em especial a Geometria Hiperbólica. O objetivo da investigação é analisar se o ensino da Geometria Hiperbólica contribui para a ampliação dos conhecimentos geométricos não euclidianos de estudantes de uma universidade pública do norte do Paraná. Para tanto, inicialmente, foi realizada uma breve reconstrução histórica a respeito do surgimento das Geometrias Não Euclidianas, investigando desde a questão do quinto postulado, presente no livro Os Elementos de Euclides, até os trabalhos de Lobachevsky e Bolay, sistematizadores da Geometria Hiperbólica, sendo apresentadas algumas características da mesma, bem como os modelos utilizados para seu estudo. Foi desenvolvida uma sequência de atividades envolvendo a Geometria Hiperbólica utilizando como recurso tecnológico o software NonEuclid. Por fim, foi realizada a análise textual discursiva dos resultados oriundos da aplicação da sequência de atividades, evidenciando, que o ensino da Geometria Hiperbólica contribui para o aprofundamento do conhecimento geométrico. |
ABSTRACT: This article discusses a research conducted in the context of teaching of Geometries Non-Euclidean, in particular Hyperbolic Geometry. The aim of the research is to analyze if the teaching of Hyperbolic Geometry contributes to the expansion of knowledge non-Euclidean geometric of students from a public university in northern Paraná. Therefore, initially, a brief historical reconstruction was done about the emergence of non-Euclidean geometries, investigating the issue since the fifth postulate, present in the book Euclid's Elements, to the work of Lobachevsky and Bolay, systematizes of hyperbolic geometry and are presented some characteristics of it, and the models used for it study. It was developed a sequence of activities involving the Hyperbolic Geometry using technological resources as the NonEuclid software. Finally has been held to discursive textual analysis of the results of implementing the sequence of activities, showing that the teaching of hyperbolic geometry contributes to the deepening of geometrical knowledge. |
1. Introdução
O surgimento das Geometrias Não Euclidianas ocorreu no início do século XIX mediante as tentativas de provar o quinto postulado de Euclides (±330 a.C. – ± 275 a.C.), conhecido como postulado das paralelas. Porém, antes disso, vários matemáticos se empenharam em provar tal postulado chegando a sistematizarem "novas Geometrias".
Uma dessas Geometrias é a Hiperbólica, desenvolvida teoricamente por Lobachevsky e Bolyai e que será foco de estudo nesse artigo. A abordagem dessa Geometria é apontada nas Diretrizes Curriculares Orientadoras da Educação Básica de Matemática do Estado do Paraná para ser trabalhada com alunos da Educação Básica. Levando em consideração o recente desenvolvimento dessa Geometria e a recomendação de documentos oficiais do Estado do Paraná para o ensino da mesma, neste artigo buscar-se-á responder a seguinte pergunta: O ensino da Geometria Hiperbólica contribui para uma ampliação de conceitos geométricos não euclidianos?
Para responder a tal pergunta foi elaborada uma sequência de atividades visando explorar a Geometria Hiperbólica, na qual foram utilizadas em algumas atividades materiais manipulativos simulando um dos modelos da Geometria Hiperbólica – pseudoesfera e, também, utilizado o software de geometria dinâmica NonEuclid, que corresponde a outro modelo desenvolvido para essa Geometria – disco de Poincaré. Tal sequência foi aplicada em uma turma do segundo ano de um curso de licenciatura em Matemática localizado em uma universidade do norte do Paraná.
Esta pesquisa é qualitativa, pois segundo Bogdan e Biklen (1994) este tipo de pesquisa apresenta como ambiente natural a fonte direta de dados e o pesquisador é o seu principal instrumento. Os dados nesse tipo de pesquisa, ainda de acordo com Bogdan e Biklen (1994, p. 16), são "ricos em pormenores descritivos". Neste sentido a pesquisa qualitativa adotada apresenta cunho exploratório, já o método utilizado para a construção da sequência de atividades se embasou em Zabala (1998) e, para a análise dos dados, foi adotada a Análise Textual Discursiva.
2. O Quinto postulado e o surgimento das Geometrias Não Euclidianas
Euclides (±330 a.C. – ± 275 a.C.) foi um matemático grego que sistematizou os conhecimentos geométricos da sua época em Os Elementos, tal obra é constituída de 13 livros ou capítulos (Boyer, 2010; Eves, 2011).
No Livro I de Os Elementos, Euclides apresenta cinco postulados, a saber:
- Fique postulado traçar uma reta a partir de todo ponto até todo ponto.
- Também prolongar uma reta limitada, continuamente, sobre uma reta.
- E, com todo centro e distância, descrever um círculo.
- E serem iguais entre si todos os ângulos retos.
- E, caso uma reta, caindo sobre duas retas, faça os ângulos interiores e do mesmo lado menores do que dois retos, sendo prolongadas as duas retas, ilimitadamente, encontrarem-se no lado do qual estão os menores do que dois retos (Bicudo in Euclides, 2009, p. 98).
O quinto postulado, conhecido como postulado das paralelas, atualmente é enunciado da seguinte forma: "Por um ponto P exterior a uma reta m, considerada em um mesmo plano, existe uma única reta paralela à reta m" (Coutinho, 2001, p. 35). Um enunciado equivalente a esse também foi dado por John Playfair (1748 – 1819).
Os postulados enunciados por Euclides compreendem afirmativas simples e evidentes, porém, como ressalta Carmo (1987), o quinto postulado não segue essa característica. Diante disso, muitos matemáticos tentaram provar esse postulado, como Ibn-al-Haitham (±965 – 1039), Nasir Eddin al-Tusi (1021 – 1274), John Wallis (1616 – 1703), Girolamo Saccheri (1667 – 1733) e Johann Heinrich Lambert (1728 – 1777).
Das tentativas feitas pelos matemáticos citados acima as que foram apresentadas por Saccheri e Lambert mostram indícios do surgimento das Geometrias Não Euclidianas. Contudo, a sistematização da mesma veio aparecer apenas no século XIX, sendo descoberta de forma independente por Nicolai Ivonovich Lobachevsky (1793 – 1856) e Jonas Bolyai (1802 – 1860).
Todavia, antes desses matemáticos, Carl Friedrich Gauss (1777 – 1855), segundo Carmo (1987), conhecia as ideias iniciais da Geometria Não Euclidiana, isso pode ser evidenciado em uma carta escrita a Taurinos em 1824:
A hipótese que a soma dos ângulos internos de um triângulo é menor que 180° conduz a uma geometria separada, totalmente diferente de nossa geometria (euclidiana), que é em si própria inteiramente satisfatória para mim, de tal modo que posso nela resolver qualquer problema, exceto a determinação de uma constante que não pode ser fixada a priori (Sjöstedt, 1968, p.341-342 apud Carmo, 1987, p. 31).
Diante do que foi exposto, fica claro que Gauss tinha ideia dessa nova Geometria e que se tratava da Geometria Hiperbólica. Mesmo de posse do conhecimento de uma nova geometria Gauss não a publicou, provavelmente devido ao receio da não aceitação de uma Geometria que não fosse a de Euclides (Arcari, 2008; Barbosa, 2002; Carmo, 1987).
Lobachevsky, diferente de Gauss, demonstrou mais confiança em suas descobertas, dedicando mais de vinte anos a esse trabalho. Ele escreveu e publicou artigos, livros a respeito da nova Geometria, sendo que em 1829 publicou um artigo no Kazan Messenger que marca o "nascimento oficial da geometria não euclidiana" (Boyer, 2010, p. 360). Neste artigo Lobachevsky mostrou uma hipótese que conflitava com o postulado das paralelas: "por um ponto C fora de uma reta AB podem ser traçadas mais de uma reta no plano que não encontram AB" (Boyer, 2010, p. 360).
O matemático por meio desse "novo postulado" deduziu uma geometria por ele denominada de Geometria Imaginária, que se refere à Geometria Hiperbólica. Com o intuito de trazer alguma atenção à sua obra escreveu alguns livros sobre ela, sendo que um ano antes de sua morte editou o livro Pangeometria, no qual escreveu todos os resultados por ele encontrados sobre essa Geometria. Devido a esse livro, essa nova Geometria é conhecida como Geometria de Lobachevsky (Barbosa, 2002; Boyer, 2010; Coutinho, 2001).
Sem ter conhecimento das descobertas de Gauss e Lobachevsky, Janos Bolyai buscava provar o quinto postulado utilizando a negação do mesmo chegando a duas hipóteses possíveis: "Primeiramente, poderia não existir qualquer reta paralela a uma reta dada, passando por um ponto fora desta reta. [...]. Segundo, poderia haver mais de uma reta paralela à reta dada passando pelo ponto" (Barbosa, 2002, p. 46).
Observando essa segunda hipótese Janos chegou a essência da nova Geometria. Essas conclusões como visto por Bolyai, não dependiam do quinto postulado e serviam para qualquer Geometria, neste sentido ele desenvolveu a "Ciência Absoluta do Espaço" (Boyer, 2010, p. 361).
Janos mandou suas conclusões a seu pai Farkas, que as publicou em forma de apêndice em seu tratado denominado Tentamen em 1829, mas só apareceu em 1832 (Barbosa, 2002; Boyer, 2010).
As considerações desses matemáticos – Gauss, Lobachevsky e Bolyai – são referentes à Geometria Hiperbólica que será descrita no próximo tópico.
3. Geometria Hiperbólica
A denominação Geometria Hiperbólica foi dada primeiramente por Felix Klein (1849 – 1925), em 1871 (Eves, 2011). Essa Geometria admite os quatro primeiros postulados apresentados por Euclides, sendo que o quinto postulado, fica enunciado da seguinte forma: "Por um ponto P fora de uma reta r passa mais de uma reta paralela à reta r" (Coutinho, 2001, p. 40).
Além disso, na Geometria Hiperbólica, diferentemente da Euclidiana, a soma dos ângulos internos de um triângulo é menor que dois retos (Barbosa, 2002; Boyer, 2010).
Essa nova Geometria, assim como Gauss havia imaginado, sofreu certas resistências e apenas em 1868, Eugenio Beltrami (1835 – 1900) provou que essa Geometria era tão consistente quanto a Geometria de Euclides por meio de um modelo no qual os resultados encontrados por Lobachevsky eram demonstrados (Carmo, 1987). Tal modelo será abordado no próximo tópico, bem como outros modelos desenvolvidos para a Geometria Hiperbólica.
3.1 Modelos de Geometria Hiperbólica
O primeiro modelo matemático para a Geometria Hiperbólica foi apresentado por Beltrami, e é denominado de pseudoesfera, o mesmo é uma superfície gerada pela resolução de uma curva tratriz em torno de sua assíntota, a superfície assim gerada apresenta curvatura negativa constante (Boyer, 2010).
Esse modelo, como ressaltado por Carmo (1987), possuía um defeito, as superfícies negativas da época apresentavam certas arestas, o que impedia que algumas retas hiperbólicas fossem prolongadas indefinidamente, assim contradizendo o segundo postulado de Euclides.
Um modelo mais satisfatório para essa Geometria, como apontado por Carmo (1987), é o de Félix Klein. Neste modelo é utilizado um círculo com as extremidades excluídas considerando apenas a região interior do mesmo, e as retas como cordas do círculo (Coutinho, 2001).
Outro modelo foi criado por Henri Poincaré (1854 – 1912), que difere do modelo de Klein apenas no que se refere às retas, pois as retas no modelo proposto por Poincaré "são arcos de círculos perpendiculares ao círculo" (Coutinho, 2001, p. 44).
No próximo tópico será tratado o uso do software NonEuclid, tal software representa o disco de Poincaré.
4. Uso do software NonEuclid como recurso ao ensino da Geometria Hiperbólica
O uso de novas tecnologias como os softwares, por exemplo, segundo Kenski (2007), trouxe mudanças consideráveis para a educação, já que a abordagem com as mesmas dinamizam as aulas, possibilitando diversificadas formas dos alunos relacionarem o conhecimento e aprenderem.
Nesta perspectiva, o uso de softwares na Educação, como ressaltado por Valente (1999), pode favorecer a construção do conhecimento, uma vez que o aluno ao utilizá-los busca novas informações para complementar ou alterar o que ele já conhece, e ao refletir a respeito do uso dessas informações cria suas próprias soluções, conclusões.
Desse modo, com a finalidade de abordar algumas noções da Geometria Hiperbólica, será usado o software NonEuclid.
O software NonEuclid é livre, desenvolvido por Joel Castellanos (Departamento de Ciência da Computação, Universidade do Novo México); Joe Dan Austin (Departamento de Educação, Universidade Rice) e Ervan Darnell (Departamente de Ciência da Computação, Universidade Rice). Tal software atualmente é traduzido apenas em inglês e italiano, porém, a linguagem do software é simples e de fácil compreensão para os alunos.
O NonEuclid é um aplicativo Java para construções interativas da Geometria Hiperbólica no disco e também no semiplano de Poincaré [3].
As possibilidades apresentadas pelo software NonEuclid permite utilizá-lo como um recurso ao ensino da Geometria Hiperbólica por abordar de forma dinâmica as características da mesma, bem como, aprofundar o conhecimento geométrico.
5. Procedimentos Metodológicos
5.1 Sequência de atividades
Para atingir o objetivo deste artigo foi desenvolvida uma sequência de atividades para o ensino do conhecimento relativo à Geometria Hiperbólica, a partir do uso do software NonEuclid.
Uma sequência de atividades, segundo Zabala (1998, p. 18), é "um conjunto de atividades ordenadas, estruturadas e articuladas para a realização de certos objetivos educacionais, que têm um princípio e um fim conhecidos tanto pelos professores como pelos alunos".
Para o autor, a sequência de atividades corrobora para o desenvolvimento de uma aprendizagem de forma significativa, tal aprendizagem refere-se ao momento em que o aluno consegue estabelecer relações entre os conhecimentos prévios e os que adquiriram.
Foi proposto aos estudantes uma sequência com dez atividades que abordavam o surgimento da Geometria Não Euclidiana, mais especificamente, a Geometria Hiperbólica. Porém nesse artigo, serão descritas e analisadas apenas cinco atividades, as quatro primeiras e a última, e o comentário dos estudantes acerca do uso do software NonEuclid. A escolha do corpus de análise se deu por essas atividades representarem as demais de forma satisfatória e ser suficiente para analisar o objetivo almejado pelo artigo.
As três primeiras atividades referem-se aos postulados de Euclides, nelas busca-se ver como os estudantes argumentam sobre os postulados e sobre suas representações.
A quarta atividade aborda o surgimento da Geometria Hiperbólica, apresentando como é descrito o quinto postulado. Nesta atividade é solicitada a demonstração desse postulado na pseudoesfera, tal modelo foi representado por meio de um material manipulativo.
A última atividade refere-se às conclusões dos alunos frente à soma dos ângulos internos de um triângulo hiperbólico, construído no software NonEuclid. Espera-se nessa atividade que eles consigam sistematizar a característica dos triângulos hiperbólicos.
5.2 Análise da sequência de atividades
Para a realização da análise da sequência de atividades optou-se por utilizar a Análise Textual Discursiva, que de acordo com Moraes e Galiazzi (2007, p. 7), tem como finalidade "produzir novas compreensões sobre os fenômenos e discursos".
Tal análise, segundo Moraes e Galiazzi (2007), pode ser organizada em três momentos que compõe um ciclo, sendo estes os elementos principais da análise:
- Desmontagem dos textos, também denominada desconstrução e unitarização. Nesse momento foram criadas as unidades de análise, por meio das características que buscávamos encontrar nas atividades, para tanto se baseou no referencial utilizado para elaborar o trabalho.
- Estabelecimento de relações: Depois de elaboradas as unidades em que seriam "colocados" os dados analisados foram criadas as categorias de análise. Essas categorias foram elaboradas, buscando comparar as unidades de análise levando em conta aspectos semelhantes que elas possuíam.
- Captando o novo emergente: Ao término da análise foi escrito o metatexto. Nessa produção foi descrita a interpretação obtida por meio da análise dos dados. Foi usada a fundamentação teórica que contribuiu para a elaboração do trabalho para auxiliar nessa interpretação, realizando-se assim, "um modo de teorização dos fenômenos investigados" (Moraes; Galiazzi, 2007, p. 32).
6. Análise dos Resultados
Neste tópico será apresentada a análise da aplicação da sequência de atividades desenvolvida em uma turma do segundo ano de Licenciatura em Matemática, de uma universidade pública do norte do Paraná, à luz da Análise Textual Discursiva.
A turma em que foi realizada a aplicação possuía doze estudantes, entretanto apenas cinco participaram de todas as atividades, dentre eles um homem e quatro mulheres, sendo que todos esses participantes já haviam cursado a disciplina de Geometria mais de uma vez.
Para compor o corpus da análise foram utilizadas cinco atividades desenvolvidas por esses estudantes. Com a finalidade de facilitar a análise foram adotados os seguintes códigos:
- E1, E2, E3... que indicam os cinco estudantes participantes da pesquisa.
- A1, A2, A3... para indicar as atividades que foram analisadas em cada unidade.
- P1, P2, P3... para indicar os cinco postulados.
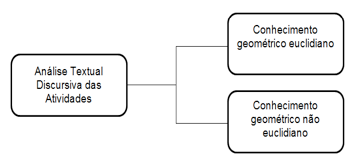
Ao analisar os dados oriundos da aplicação foram elencadas duas categorias prévias, a saber: Conhecimento geométrico euclidiano, que visa analisar os conhecimentos que os estudantes possuem referente à Geometria Euclidiana; Conhecimento geométrico não euclidiano, que tem em vista investigar se houve um aprofundamento em relação ao conhecimento geométrico.
|
Figura 1: Categorias prévias da Análise Textual Discursiva |
A categoria prévia "conhecimento geométrico euclidiano" apresentou uma subcategoria: representação e compreensão dos postulados, que buscava ver como os estudantes representam e compreendem os cinco postulados de Euclides.
|
Figura 2: Subcategoria de análise do conhecimento geométrico euclidiano |
Na subcategoria foram previstas três unidades de análise, como apresentada na Figura 3:
|
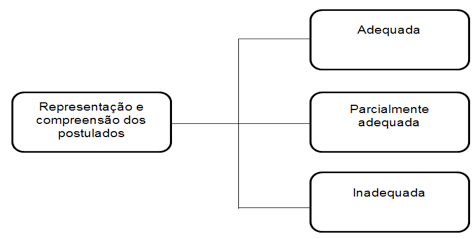
Figura 3: Unidades de análise prévias da Representação e compreensão dos postulados |
Na subcategoria representação e compreensão dos postulados foram previstas três unidades de análise, contudo, foi necessário criar uma unidade emergente, referente a não representação do quinto postulado.
Subcategoria: Representação e compreensão dos postulados Nesta subcategoria buscou-se analisar como os estudantes representam e compreendem os cinco postulados apresentados no livro I de Euclides, intitulado Elementos. Foi utilizada para análise desta subcategoria a A1, A2 e A3. |
Unidade: Adequada Nesta unidade é verificado se os estudantes interpretaram e representaram adequadamente os postulados de Euclides. |
"Somente os quatro primeiros postulados tem uma linguagem de fácil interpretação, o quinto postulado já fica uma linguagem um pouco mais confusa [...]" (A1, E1).
"Os 4 primeiros sim são evidentes, o 5° postulado se for referente a Geometria Euclidiana é evidente, por aplicar em uma superfície plana, no entanto, na geometria não-Euclidiana, já não é aceito, pois trabalharia com superfícies curvas" (A1, E2)
"Não estão evidentes em alguns postulados, mas alguns postulados podem ser identificados e até mesmo visualizados. No postulado 5 não consigo nem ao menos tive algum entendimento". (A1, E3)
"Sim, no meu ponto de vista os postulados 1, 2, 3, 4 são simples e evidentes. Já o postulado 5 achei complexo e não muito de acordo". (A1, E5)
"No quinto postulado Euclides explica uma reta (não especificando que tipo) no entanto, John refere-se a duas retas paralelas, ou seja, m//m' e
|
"Através de dois pontos obtém-se uma reta" (A2, E1).
"Traçar uma reta a partir do ponto A até o ponto B" (A2, E2).
"Esta construção parece ser bem simples, pois dá passos a serem feitos" (A2, E3).
"Se há dois pontos distintos então ali há uma reta" (A2, E4).
"Tracei uma única reta" (A2, E5).
"A reta pode ser dividida em vários segmentos de reta" (A2, E4)
"Centro da figura (ponto A) ao ponto B". (A2, E1).
"Fiz um circulo" (A2, E5).
"Nesta construção, como são dados um ponto e direção pode a partir disso montar um círculo em sua volta" (A2, E3)
"A partir do centro O com distância
"A distância no caso é o raio, com um ponto central e raio se descreve um circulo" (A2, E4).
"Duas retas com ângulos retos" (A2, E5).
"
"Se o ângulo é reto tem que ter 90°. Nem mais e nem menos" (A2, E4).
"Ângulos
"O lado que tiver o ângulo menor está convergindo de encontro até interceptar" (A2, E4).
|
Unidade: Parcialmente adequada Nesta unidade será analisado se os estudantes interpretaram e/ou representaram parcialmente adequados os postulados de Euclides. |
"Sim, pois são verdades irrefutáveis dentro da Geometria euclidiana" (A1, E4).
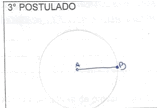
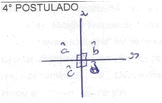
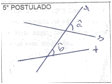
"Os dois postulados tem retas paralelas e um ponto que corta as duas retas" (A3, E1).
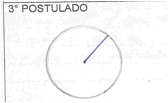
"Uma reta paralela a outra" (A3, E5).
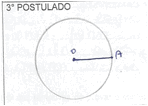
"Pois só pode haver uma reta com 90° entre si em toda extensão que passa pelo ponto P externo a reta m" (A3, E4).
"Encontro de duas retas, forma-se o ângulo" (A2, E1).
"Duas retas concorrentes que se encontram em um determinado ponto" (A2, E1).
"Uma reta caindo sobre duas retas, não entendi, consegui visualizar certo os ângulos" (A2, E5). |
Unidade: Inadequada Nesta unidade será apurado se os estudantes interpretaram e/ou representaram incorretamente os postulados presente em os Elementos. |
"[...] entendi que havia duas retas paralelas que cortavam a reta m e que no plano havia um ponto externo que não interferia entre as retas" (A3, E3).
"Por uma reta passam vários pontos" (A2, E1).
"traçar uma reta r, e sobre a reta r traçar reta s tendo em comum o ponto A, ou seja,
"Prolonguei essa mesma reta" (A2, E5).
"Nesta construção, podemos considerar que são retas paralelas, mas com limitações" (A2, E3)
"Neste postulado pode se entender que tem uma reta vertical e traçar duas retas horizontais" (A2, E3) |
Unidade: Não apresentou representação |
"Não construí este postulado, pois não entendi. Não consegui identificar o que foi pedido" (A2, E3, P5) |
Quadro 1: Unidades efetivadas da subcategoria Representação e compreensão dos postulados |
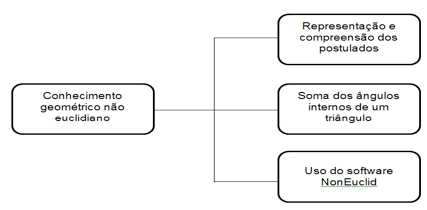
A categoria prévia "conhecimento geométrico não euclidiano" foi dividida em três subcategorias: representação e compreensão do quinto postulados, que busca ver como os estudantes representam e compreendem esse postulado na Geometria Hiperbólica; soma dos ângulos internos de um triângulo, que visa verificar o conhecimento dos estudantes sobre a soma dos ângulos de um triângulo na Geometria Hiperbólica e uso do software NonEuclid, que almeja constatar se a utilização do software auxiliou na compreensão da Geometria Hiperbólica.
|
Figura 4: Categoria Conhecimento geométrico não euclidiano e subunidades prévias |
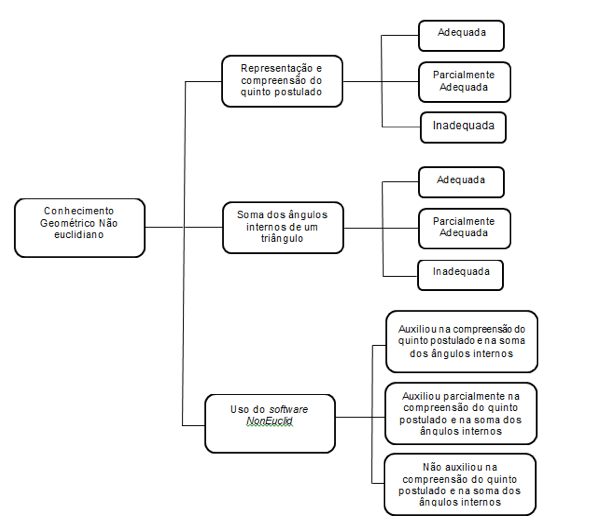
As três subcategorias elencadas foram subdivididas em nove unidades de análise.
|
Figura 5: Categoria Conhecimento geométrico não euclidiano, subcategorias e unidades de análise prévias. |
Na subcategoria representação e compreensão do quinto postulado foram efetivadas apenas duas unidades de análise: adequada e parcialmente adequada.
Subcategoria: Representação e compreensão do quinto postulados Nesta subcategoria buscou-se analisar como os estudantes representam e compreendem o quinto postulado da Geometria Hiperbólica. Foi utilizada para análise desta subcategoria a A4. |
Unidade: Adequada Nesta unidade será verificado se os estudantes interpretaram e representaram adequadamente o quinto postulado da Geometria Hiperbólica. |
A partir de demonstração do postulado na pseudoesfera ficou comprovado que podem ser traçadas várias retas paralelas que não se encontram com a reta principal, pois o plano de curvatura negativa não permite (A4, E2).
A partir da demonstração do quinto postulado, pode ser observado que existe mais de uma reta paralela de sua reta principal (A4, E3).
Que por um ponto externo a uma reta em curvatura negativa se tem infinitas retas paralelas (A4, E4).
|
Unidade: Parcialmente adequada Nesta unidade será verificado se os estudantes interpretaram e/ou representaram parcialmente adequada os postulados de Euclides |
Na demonstração pode-se comprovar que no plano passam-se várias retas. (A4, E1).
Consegui visualizar que as retas não se encontram, e que por um ponto pode ser traçadas mais de uma reta (A4, E5). |
Quadro 2: Subcategoria Representação e compreensão do quinto postulado e Unidades efetivadas |
Na subcategoria soma dos ângulos internos de um triângulo foram efetivadas apenas as unidades de análise adequada e parcialmente adequada.
Subcategoria: Soma dos ângulos internos de um triângulo Nesta subcategoria buscou-se analisar o conhecimento dos estudantes frente à soma dos ângulos internos de um triângulo hiperbólico. Foi utilizada para análise desta subcategoria a A10. |
Unidade: Adequada Nesta unidade será verificado se os estudantes interpretaram e representaram adequadamente a soma dos ângulos internos na Geometria Hiperbólica. |
Diante a relação entre a Geometria Euclidiana e Hiperbólica a soma dos ângulos internos da G. Hiperbólica é menos que 180° (A10, E1).
A soma dos ângulos internos são menores que 180° [...] (A10, E2).
Na geometria Hiperbólica as somas dos ângulos internos são inferiores em relação a geometria Euclidiana [...]. Na Geometria Hiperbólica quanto mais ao extremo do disco menores os ângulos e quanto mais no centro maior os valores dos ângulos (A10, E3).
Que quando mais próximo dos extremos do disco de Poincaré menores são os ângulos e consequentemente menor será a soma dos ângulos internos do triângulo e, se estiverem os 3 pontos formadores do triângulo mais próximos do centro do disco de Poincaré, mais próximo de 180° será a somatória dos ângulos internos deste triângulo (A10, E4).
|
Unidade: Parcialmente adequada Nesta unidade será verificado se os estudantes interpretaram e/ou representaram parcialmente adequada à soma dos ângulos internos na Geometria Hiperbólica |
Na Geometria Hiperbólica a soma dos ângulos dão diferentes (A10, E5) |
Quadro 3: Subcategoria Soma dos ângulos internos de um triângulo e unidade efetiva de análise |
Na subcategoria uso do software NonEuclid foi efetivada apenas a unidade de análise auxiliou na compreensão do quinto postulado e na soma dos ângulos internos de um triângulo.
Subcategoria: Uso do software NonEuclid Nesta subcategoria buscou-se analisar a contribuição do uso do software NonEuclid, na execução das atividades. Para tanto foi utilizado para análise os comentários feitos por escrito dos estudantes. |
Unidade: Auxiliou na compreensão do quinto postulado e na soma dos ângulos internos de um triângulo. |
O software utilizado proporcionou uma melhor compreensão e visualização dos [...] dos postulados. Os gráficos apresentados se tornam mais detalhados, e isso facilita a visualização (E1).
A utilização do software NonEuclid [...] possibilita uma visualização dessas demonstrações graficamente, sendo assim, o software contribuiu para unificação da teoria com a visualização, perfeitamente. Com isso contribui imensamente para o ensino e aprendizagem da nova geometria (E2).
Com a utilização do software NonEuclid houve uma melhor interpretação e visualização [...], podendo ter uma visão mais ampla do que foi trabalhado. O software permite ter uma noção melhor do quinto postulado [...] (E3).
A utilização do software tira a abstração da informação, consegue solidificar, tornar visual um algo que o aluno não tem maturidade de abstração, raciocínio ou não tem conhecimento do conteúdo [...] (E4).
O uso software NonEuclid, me ajudou para um maior entendimento da Geometria Hiperbólica (E5). |
Quadro 4: Subcategoria Uso do software NonEuclid e unidade efetivas de análise |
6.1 Síntese da análise dos dados: O Metatexto
A primeira categoria visava analisar o conhecimento geométrico euclidiano dos estudantes participantes da pesquisa. Essa categoria contemplou somente uma subcategoria, referente à compreensão e representação dos postulados euclidianos, com a intenção de analisar como os estudantes compreendem e representam os cinco postulados apresentados por Euclides em seu livro Elementos.
Essa subcategoria foi subdividida em três unidades de análise, que sopesaram se a compreensão e a representação dos postulados euclidianos estão adequadas, parcialmente adequadas, inadequadas e se não havia representação alguma. Com isso, observou-se que os estudantes em alguns postulados (P2 e P5) apresentaram um pouco mais dificuldade em relação a sua compreensão bem como na sua representação, algumas respostas foram enquadradas como parcialmente adequadas (P5) e inadequadas (P2). Todavia, esses mesmo postulados também foram representados de forma adequada por alguns estudantes (P2, E4; P5, E2 e E4). Nessa subcategoria também houve uma não representação devido à falta de entendimento pela linguagem do quinto postulado (A1, E3). Em sua maioria, os estudantes apresentaram respostas parcialmente adequadas quando foram solicitados a fazer comparação da representação do quinto postulado de Euclides e o postulado equivalente de Playfair.
A segunda categoria da análise é referente ao conhecimento geométrico não euclidiano, tal categoria visava averiguar se os estudantes aprofundaram seus conhecimentos geométricos. Para especificar mais essa categoria, subdividiu-a em subcategorias, assim como foi feito na categoria anterior. A primeira subcategoria é sobre a representação e a compreensão do quinto postulado na Geometria Hiperbólica, a fim de analisar como os estudantes representam e compreendem o quinto postulado em tal Geometria. Para tanto como unidade de analise foi visto se estavam adequadas e parcialmente adequadas as respostas dadas pelos estudantes. A maioria dos estudantes respondeu adequadamente como é o quinto postulado na Geometria Hiperbólica, apenas E1 e E3 responderam de forma parcialmente adequada, isso devido a forma como tais estudantes escreveram. Em relação à representação desse postulado, todas as representação foram adequadas.
A segunda subcategoria, referente à soma dos ângulos internos de um triângulo na Geometria Hiperbólica, visava investigar se os estudantes compreenderam o que ocorre com a soma dos ângulos internos de um triângulo hiperbólico. Nessa subcategoria em sua maioria os alunos responderam adequadamente a tal questão, sendo que apenas E5 apresentou resposta parcialmente adequada.
Na terceira e última subcategoria foi analisada a contribuição do uso do software NonEuclid frente ao quinto postulado e à soma dos ângulos internos de um triângulo na Geometria Hiperbólica. Essa subcategoria efetivou apenas uma unidade de análise: Auxiliou na compreensão do quinto postulado e na soma dos ângulos internos de um triângulo, o que demonstra que os participantes da pesquisa acharam válido o uso do software no ensino da Geometria Hiperbólica, uma vez que o mesmo os auxiliou na compreensão dessa Geometria (E2 e E5), por possibilitar a visualização do que foi abordado nas atividades (E1, E2, E3, E4).
Por meio da descrição realizada da análise foi possível constatar que na categoria conhecimento geométrico euclidiano, os estudantes envolvidos na pesquisa apresentaram um conhecimento satisfatório. Porém, ao longo das atividades alguns estudantes apresentaram certas dificuldades na interpretação e representação de alguns postulados, no caso do P2 e P5.
Em relação ao quinto postulado, os mesmos verificaram que tal postulado não era tão simples e evidente, assim como explicitado por Carmo (1987), e por meio da realização das atividades foram levados a perceber que mediante as tentativas de provar o quinto postulado surgiu as Geometrias Não Euclidianas (Arcari, 2008; Barbosa, 2002, Coutinho, 2001).
Na segunda categoria Conhecimento Geométrico Não Euclidiano foi possível ver um aprofundamento no conhecimento geométrico dos estudantes, uma vez que os mesmos realizaram satisfatoriamente as atividades propostas, conseguindo sistematizar o que lhes foi proposto.
Quanto aos recursos utilizados, como a representação da pseudoesfera e do software NonEuclid, foi possível notar que ambos auxiliaram no processo, já que os estudantes puderam testar e comprovar as características da Geometria Hiperbólica. Em relação ao software ele possibilitou que as atividades fossem realizadas de forma dinâmica (Kenski, 2007), pois contribuía para a busca de informações para complementar ou alterar o que os estudantes já conheciam (Valente, 1999).
7. Considerações Finais
O trabalho evidenciou uma possibilidade de se trabalhar as Geometrias Não Euclidianas, mais especificamente a Geometria Hiperbólica, por meio de uma sequência de atividades, na qual foi adotada uma perspectiva histórica, o uso de materiais manipuláveis e o uso do software NonEuclid. Tal perspectiva foi utilizada com intuito de mostrar que a humanidade desenvolveu outras Geometrias com características próprias, além de deixar a compreensão desse conhecimento mais completa e ampla (Matthews, 1999).
Nesse sentido, o resultado da aplicação mostrou que a sequência de atividades forneceu um aprofundamento no conhecimento geométrico, já que os estudantes tiveram contato com a sistematização de algumas características da Geometria Hiperbólica.
Mesmo que essa sequência tenha sido aplicada em um curso de graduação, vemos a possibilidade dela ser aplicada em uma turma de Ensino Médio, já que tal assunto é previsto nas DCE do estado do Paraná (2008). Todavia, às vezes seriam necessárias algumas adaptações aos contextos sócio-temporais que ficariam a critério do docente.
Como essa aplicação ocorreu em uma turma de graduação de Matemática esperamos que esse contato possibilitasse a esses estudantes, futuros professores, o ensino das Geometrias Não Euclidianas nas salas em que atuarem.
Dessa forma, vimos com esse trabalho uma possibilidade diferente de se abordar o conhecimento geométrico não euclidiano, abordando aspectos históricos e utilizando recursos que representam os modelos utilizados na Geometria Hiperbólica, contribuindo assim, para dar maior significado a esse conhecimento matemático.
Referências
Arcari, I. Um texto de geometria hiperbólica. 2008. 136 f. Dissertação (Mestrado). Universidade Estadual de Campinas, Campinas, 2008.
Barbosa, J. L. M. Geometria hiperbólica. Goiânia. ed. da UFG, 2002.
Bogdan, R. C.; Biklen, S. K. Investigação qualitativa em educação: uma introdução à teoria e aos métodos. Porto: Porto Editora, 1994.
Boyer, C. B. História da Matemática. Tradução de Elza F. Gomide. 3. ed. São Paulo: Blucher, 2010.
Carmo, M. P. do. Geometrias Não-Euclidianas. In: Matemática Universitária, São Paulo, n 6, dezembro de 1987, p 25-48. Disponível em: < http://matematicauniversitaria.ime.usp.br/Conteudo/n06/n06_Artigo02.pdf> Acesso em: 09 jul. 2013.
Coutinho, L. Convite às geometrias não-euclidianas. 2. ed. Rio de Janeiro: Interciência, 2001.
Bicudo, I. Introdução e tradução. In: Euclides, Os Elementos. São Paulo: Editora Unesp, 2009.
Eves, H. Introdução à história da matemática. Tradução Hygino H. Domingues. 5 ed. Campinas: Editora da Unicamp, 2011.
Kenski, V. M. Tecnologias também servem para fazer educação. In: ______. Educação e Tecnologias: o novo ritmo da informação. 2 ed. Campinas: Papirus, 2007.
Matthews, M. R. História, Filosofia e Ensino de Ciências: A Tendência Atual de Reaproximação. Caderno Catarinense de Ensino de Física, v. 12, n. 3: p. 164-214, dez. 1995.
Moraes, R.; Galiazzi, M. do. Análise textual discursiva. Ijuí: Ed. Unijuí, 2007.
Paraná. Diretrizes Curriculares da Educação Básica Matemática. SEED, Curitiba, 2008.
Software NonEuclid. Disponível em: <http://www.cs.unm.edu/~joel/NonEuclid/NonEuclid.html> Acesso em: 30 maio 2013.
Valente, J. A (Org.). O computador na sociedade do conhecimento. Campinas: Nied, 1999.
Zabala, A. A Prática Educativa: Como ensinar. Tradução Ernani F. da F. Rosa - Porto Alegre: ArtMed, 1998.
* Este artigo é resultado de uma pesquisa de Especialização em Educação Matemática, desenvolvido na Universidade Estadual do Norte do Paraná, Campus Cornélio Procópio.
1. Universidade Estadual de Londrina: marianylayne@hotmail.com
2. Universidade Estadual do Norte do Paraná, Campus Cornélio Procópio: simoneluccas@uenp.edu.br
3. Nesse trabalho optou-se pelo uso apenas do disco de Poincaré para serem realizadas as atividades.

 (A3, E2)
(A3, E2)








 (A3, E1)
(A3, E1) (A3, E5)
(A3, E5) (A3, E4)
(A3, E4)