1. Introduction
Competitiveness, identified in various segments of society, is also increasing on the world stage of tourism. A growing number of consumers have access to tourism, fostering the economic rise of developed and emerging destinations (COSHALL; CHARLESWORTH, 2011).
Destination choice, in general, does not only focus on natural and cultural attractions. The choice of a certain route permeates factors such as planning, organization of cities and tourism infrastructure, which are attractive to the increased flow of travelers. Knowing the behavior of tourists, identifying their needs as well as sizing an expected number are components that help administrators in processes involving the reception of such visitors. According to Ballou (2004), demand forecasts are often included in the planning and control of such processes. Forecasting the demand of tourists increases chances to adequately meet the expectations of such consumers.
The use of quantitative methods is being applied to obtain estimates in the forecasting of tourism demand in parallel with the development and improvement of the forecasting techniques (WONG et al., 2008). Song and Li (2008) concluded, in their study of reviewed literature on forecasting in tourism that, although many studies indicate that more sophisticated forecasting methods promote improvement in accuracy, there is no clear evidence attesting to the superiority of these techniques for tourism. Furthermore, these authors also concluded that despite the emphasis of seasonal behavior on the studies about series of tourism demand, it is not clear in the results which treatments can be applied to such behavior in order to improve forecasting. The authors suggest a scarcity in the development of forecasting methods that can accommodate unexpected or occasional events such as disasters or the soccer World Cup, for instance. For the tourism industry, the incorporation of methods of forecast adjustment may represent a differentiation in the exactitude achieved, once they are usually obtained through more accurate methods than the individual forecasts.
However, reliable forecasts may call for the use of a variety of techniques, providing the greatest amount of information available. The method of combination forecasts represents a way of connecting forecasts obtained from different forecasting techniques. It is also possible to integrate forecasts by performing an adjustment based on opinion, using information from the environment itself (WERNER, 2005). The application of these forecasting methods is an alternative search for greater accurateness vis-à-vis the seasonality of tourism.
Before hosting an event as specific as the soccer World Cup, it is essential to identify processes that minimize error forecasting. Hence, the objective of this work is to propose an alternative to the forecasting of tourists in the World Cup in Brazil. So as to make it happen, there will be an application of the method of combination forecasts with adjusted data, in a series of tourism demand for countries in periods of soccer World Cup. The individual forecasting techniques used are ANN (Artificial Neural Networks) and the Box-Jenkins methodology. The final forecast will be achieved through the combination method of minimum variance with a subsequent mathematical adjustment.
The framework for this paper is thus organized: introduction and the objective of the topic in the initial section; description of the forecasting methods used in this study in the second section; method used to achieve the goals in the third section; results in the fourth section; conclusions in the section.
2. Literature Review
2.1 Individual forecasts
The methodology described by Box and Jenkins in the 70's is based on the adjustment of the data set to the autoregressive integrated moving average models ARIMA (p, d, q) (MORETTIN; TOLOI, 2006). According to Khashei and Bijari (2010), this approach has prevailed for many years in many forecasting areas. In order to build the model, Box et. al (1994) presented four stages: Specification, Identification, Estimation, Verification.
Different models can be identified through the Box-Jenkins methodology, among which are the autoregressive integrated moving average models of order p, d, q (ARIMA) and the Seasonal Autoregressive Integrated Moving Average order, p, d, q, P, D, Q with seasonal season s (SARIMA).
The class of seasonal ARIMA models (SARIMA) is formed of a non-seasonal order (p, d, q) and other seasonal order (P, D, Q)s. Chen and Wang (2007) define this as the most widely used linear model for the forecasting of seasonal time series, subject matter of many series of tourism demand. The SARIMA models are defined according to Equation (1) and the forecasts obtained for h steps forward, through this class of models, are described in Equation (2).
![]() (1)
(1)
![]() (2)
(2)
where:
![]() is the seasonal autoregressive operator of order P;
is the seasonal autoregressive operator of order P;
![]() is the seasonal autoregressive operator of order Q;
is the seasonal autoregressive operator of order Q;
![]() is the seasonal difference operator, with D indicating the number of seasonal differences;
is the seasonal difference operator, with D indicating the number of seasonal differences;
![]() is the simple difference operator, with d indicating the number of simple differences;
is the simple difference operator, with d indicating the number of simple differences;
![]() is the autoregressive operator of order p, stationary;
is the autoregressive operator of order p, stationary;
![]() is the autoregressive operator of order q
is the autoregressive operator of order q
![]() is a Gaussian white noise process, that is,
is a Gaussian white noise process, that is, ![]() .
.
The models of artificial neural networks (ANN) represent another form of analysis of a time series (HAIR et al., 2005). Such models are considered non-parametric or statistically robust (RIPLEY, 1996). The term robust is due to the fact that the models of ANN can cope with certain characteristics of data better, such as nonlinearity, for instance (FLORES, 2009). Furthermore, ANN models analyze non-stationary time series easily (DE WILDE, 1997, HAYKIN, 2001). In general, artificial neural networks have a structure that can be described by four groups: neurons (us), type of network neural model, the networks and learning.
Neurons are considered key elements in an ANN (RIPLEY, 1996, HAYKIN, 2001) because they carry out steps as input and output data. In the general model, a neuron is composed of the following elements: connections, additive junction, activation function and bias.
ANN models can be divided into different special classes, such as networks of radial basis function and multilayer perceptron (MLP). As for the format, however, it can be divided into three general classes, distinguished by operation (DE WILDE, 1997, HAYKIN, 2001), which are: feedforward networks with single layer, feedforward networks with multiple layers and recurrent networks.
Feedforward neural networks with multiple layers are considered the best known model of ANN (ZHANG, BERARDI, 2001; AUER et al., 2008). This ANN model is also considered the most popular by Qi and Zhang (2001). In this model, the network has one or more hidden layers of neurons, which are not visible in input and output layers. The great advantage of multi-layer networks is the complexity of the systems they are able to deal with, including the seasonality of time series. This is due to the increased synapse capacity offered by the hidden and output layers. The configuration of the neural network is a sequential arrangement which covers three types of layers, composed by the neurons: input, output and hidden.
Neurons receive the data and perform transmission to the neural network in the input layer. The output neuron receives input and computes an output value, named final value. In the case of the forecasting models, this value represents the forecast. The hidden layers and the activation function allow the analysis of the nonlinear models (HAIR et al., 2005).
The learning phase in the ANN is where the training system occurs. In a supervised learning mode, input and output values are compared. The errors created by such differences are used to adjust the model. The most common form of training is backpropagation, in which the error found in the output value is distributed steps backwards throughout the whole system (HAIR et al., 2005).
2.2 Combination of Forecasts and Adjustments
Combination forecast is a method employed with the aim of improving the accuracy of forecasts (COSTANTINI; PAPPALARDO, 2010). Initially presented by Bates and Granger (1969), it is considered, according to Clemen (1989), an attractive method to convey the performance of forecasts. Literature on the subject indicates that the linear combination of forecasts is usually more accurate than the individual forecasts that comprise it (CLEMEN, 1989; STOCK; WATSON, 2004; PATTON; SHEPPARD, 2009; COSTANTINI; PAPPALRDO, 2010).
Forecasting accuracy of can be improved when it is achieved through a combination of individual forecasts. This statement is feasible assuming that individual forecasting techniques originate from different approaches and can capture distinct characteristics of each series (ARMSTRONG, 2001). The combination of forecasts to be contemplated in this study is composed of the method of minimum variance. The minimum variance method proposed by Bates and Granger (1969) is a linear combination of two objective forecasts (mathematical). In this method, objective forecasts must be non-biased and the combination of individual forecasts is obtained as a result of a weight assigned to each of the individual forecasts combined. Such structure is shown in Equation (3).
where w is the weight assigned to the prediction and F1 and F2 are the individual forecasts to be combined.
The procedure for calculating the weights for each forecast described in Equation (3) is accomplished considering the error variances of the individual forecasts and the correlation between the errors of such individual forecasts. In order to give less weight to the forecasts that show a greater variability in their forecast errors, weight finding should be calculated as presented in Equation (4).
![]() (4)
(4)
where: r is the value of the linear correlation between the errors of the forecasts obtained in F1 and F2 and s2 is the variance of the forecast errors F1 and F2.
According to Goodwin (2002), all forecasting methods are connected with opinion, for it is involved in the selection of the methods to be employed. Despite the use of statistical forecasting methods, according to Bunn and Wright (1991), results are often adjusted by experts. The need to incorporate information not conveyed in a model is considered one of the main reasons to perform a forecast adjustment (BUNN; SALO, 1996).
Nevertheless, caution is indispensable when making adjustments based on opinion. When adjustments are used in order to identify patterns in time series, one can overestimate/underestimate the values or, yet, identify systematic patterns in random behaviors (GOODWIN, 2000). To avoid such effects, and increase forecast accuracy, it is beneficial to use previous knowledge, along with some structured way (SANDERS, RITZMAN, 2001; ARMSTRONG, COLLOPY, 1998). The adjustments made in this work include mathematical calculation as a way to incorporate knowledge. This calculation refers to the intrinsic knowledge in the growth / decrease rate of the number of foreign tourists in soccer World Cups. Regarding its structure, the adjustment applied to the forecast will be based on mathematical calculations derivative from similar series.
3. Methodology
The initial phase of this study included the selection of database that presented monthly series of foreign tourists arriving in the country hosting the soccer World Cup. Such data was obtained directly from officials of the governments of the countries included in this study.
The estimates begin with the analysis of the number of foreign tourists who visited Brazil from January 2003 to December 2009. The forecast is carried out monthly, and includes the ARIMA and ANN models, combined by the method of minimum variance. BIC (Bayesian Information Criterion) is the selection criterion used to choose the best model. For the models performed by the method of ANN at least one hidden layer was used. The learning of the system was obtained considering the backpropagation training.
To perform the adjustment of the forecast of tourists expected for the soccer World Cup held in Brazil, series of tourists from countries located outside the traditional headquarters of the axis of the soccer World Cups were used. The countries that meet such conditions are Uruguay (1930), Brazil (1950), Chile (1962), Mexico (1970, 1986), Argentina (1978), Japan and Korea (2002) and South Africa (2010). Based on the increasing access to tourism and behavioral changes over the decades, the analysis of this study was limited to the series of of tourists in the World Cups held in 2002 and 2010.
The series used to make forecast for countries such as South Africa, Japan and South Korea are alike in size: they include 77 periods of monthly observations. Forecasts for these countries were also generated by the ARIMA and ANN models, as well as the combination through the method of minimum variance. Such forecasts are expressed a step forward. In both cases, series with data are used until May in the year of the World Cup, so that after the model adjustment, it is possible to perform the forecast for the initial month of the World Cup (June). Obviously, the generated forecast presents a fairly high error rate due to the performance of an occasional event not contemplated by time series. This error is then measured in percentage terms. The average percentages comprise the mathematical adjustment applied to the series of forecasts of foreign tourists expected in Brazil in June 2014.
4. Results
For the series of number of foreign tourists visiting Brazil, according to data from the website of the Ministry of Tourism, ARIMA and ANN forecasts were performed and later served as basis for the combined forecasts through the minimum variance method. Such forecasts were obtained through an observation period of 84 months. Figure 1 shows the number of tourists in Brazil from 2003 to 2009, as well as the forecast performed until June 2014, period in which the World Cup will be held in Brazil. It is possible to identify stability (stationarity) of the series, with no trend of growth in this sector in Brazil over the last five years. Such behavior has been maintained in the five years forecast for the number of foreign tourists in the country.
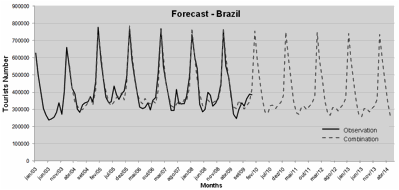
Figure 1 – Forecast for tourists in Brazil
The use of combined forecasts improved their accuracy, due to the measured values obtained through the MAPE (Mean Absolute Percentage Error) measurement. The MAPE measure scored 7.41 for the combination of forecasts, while for the ARIMA and ANN models the values scored 7.83 and 10.93 respectively.
As for occasional events, a good forecast is not enough, it is necessary to make adjustments that consider correction for the estimated value. A growing number of foreign tourists is expected in the initial period of events like the World Cup. To estimate this increase and make later adjustments, there was an evaluation of the increase in the number of foreign tourists in countries where this event was held over the past 20 years and which were geographically located out of the Europe-North America axis, including the host countries South Africa, in 2010, and Japan/South Korea, in 2002.
For this purpose, first forecasts of tourists for South Africa, Japan and South Korea were performed. Data for such forecasts was taken from their official websites (South African Tourism; Japan Tourism Marketing Co, Korea Tourism Organization). The models used for these forecasts were obtained in an analogous way for Brazil, being also used as the basis for the combining forecasts, the forecasts obtained through the ARIMA and ANN models. The observed time periods totalized 77 months for each series. Figures 2, 3 and 4 show the number of tourists and the combination forecast for each of these countries.
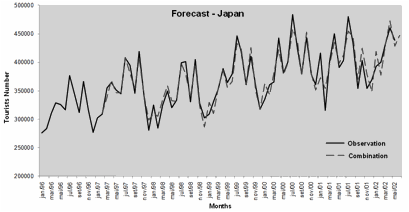
Figure 2 – Prediction of tourists to Japan
----
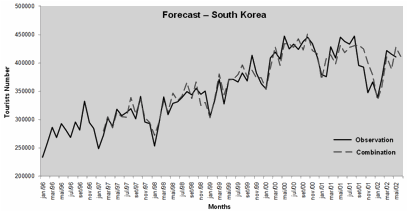
Figure 3 – Prediction of tourists to South Korea
----
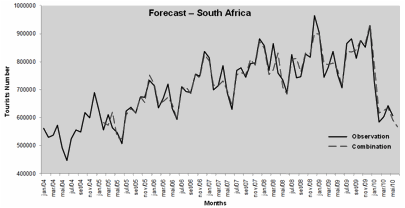
Figure 4 – Prediction of tourists to South Africa
Further on, after performing the forecasts, there was a measurement of the forecast error observed with the increase of tourists in the initial period for each location involved with the World Cup. An average error percentage was observed, in absolute values, for the forecasts made in previous periods, in this case, to the 77 monthly observations. The results presented in Table 1 show that, on average, the absolute percentage errors for the forecasts generated by foreign tourists in the countries observed in this study are close to 3%, highlighting the need to apply an adjustment to the forecasts for occasional events. The percentage forecast errors of foreign tourists got close to 27.25% for South Africa in 2010, 15.26% in Japan in 2002 and -7.96% in South Korea, also in 2002, with an average percentage of these errors resulting in 11.52%. Mathematical adjustments to be made in forecasting the number of foreign tourists expected for the soccer World Cup in Brazil are based on this average.
Table 1 – Forecast errors of foreign tourists for the initial months of the World Cup
Countries |
Forecast |
Observation |
Error |
Error % |
Average Error % |
Japan |
447.664 |
516.013 |
68.349 |
15,26% |
3,26% |
South Korea |
411.918 |
379.142 |
-32.776 |
-7,96% |
3,14% |
South Africa |
566.856 |
721.311 |
154.455 |
27,25% |
2,82% |
As for periods without the presence of special events, the average percentage of error did not exceed 3.26%. The difference between the average percentage of errors historically observed, and the percentage error in the month of the event, reinforce the justification for performing an adjustment to the forecast of tourists to June 2014, period that includes the beginning of the World Cup to be held in Brazil.
With the forecast figures for the number of tourists in Brazil in June 2014 and the average percentage error of forecasts of foreign tourists of 11.52%, it is possible to provide an estimate for the number of foreign tourists in the World Cup in Brazil in 2014.
The estimated number for June 2014 in Brazil was of 253,122 foreign tourists, using the combination of individual forecasts obtained in the study. With the application of the adjustment of 11.52% to this estimate, it is possible to obtain the adjusted value for the number of foreign tourists. With this adjustment, the expected number of foreign tourists coming to Brazil in the period of June 2014 is approximately 282,282 visitors.
5. Final Remarks
The growth of the tourism sector provides opportunities of economic rise to developed and emerging places of destination. Choices of itinerary made by tourists include, besides natural and cultural attractions, factors such as planning, organization of cities and tourism infrastructure. It is in this context that forecasts to assist managers in the processes to adequately meet the expectations of consumers become indispensable.
Forecasting performance is a process that involves errors. Forecasting demand of tourists in occasional events like the FIFA World Cup can generate even bigger mistakes. In order to minimize such errors, this study proposed a forecast with mathematical adjustment. In order to do it, forecasts were performed through ARIMA and ANN techniques which were combined by the method of minimum variance. Afterwards, the mathematical adjustment was performed, based on the forecast errors generated in the countries that hosted the World Cups in 2002 and 2010.
A gain of accuracy was observed with the use of the method of combined forecasts compared to the individual ones. For the monthly series of foreign tourists in Brazil, the measure of accuracy MAPE was calculated 7.41 for the combination, by the method of minimum variance, whereas these values were higher for the individual ARIMA (7.83) and ANN (10.93) forecasting techniques. The forecast of foreign tourists in Brazil, for June 2014, is 252,122 visitors.
It can be observed, in this study, that the percentage error for the number of foreign tourists, in the forecasting month in the host countries of the World Cup, reached 27.25% for South Africa, 15.26% for Japan and -7.96% for South Korea,. However, for specific periods without occasional events, these errors reached an average of about 3%, supporting the need to apply an adjustment to the forecast made for periods that include specific events.
The application of a mathematical adjustment to the forecast of foreign tourists visiting Brazil in June 2014 promotes the assimilation of the event to be held at that time. An estimated adjustment of a magnitude of 11.52% increase in the number of tourists has been performed, with a further forecast of 282,282 foreign visitors expected for this period.
The implementation of such projected forecast of tourists raised questions with respect to the use of other time series with other countries for further forecasts, expanding the range of tourist profile used in this study and providing opportunity for future work. In Brazil, the performance of forecasts based on simulated data and the composition of the forecast through other models also symbolize opportunities for further studies.
References
ÁFRICA DO SUL. South African Tourism – disponível em: http://www.southafrica.net/sat/content/en/us/research-home - Acesso em 15/02/2011
ARMSTRONG, J. S. (2001) Principles of forecasting: A handbook for researchers and practitioners. Kluwer Academic Publishers.
ARMSTRONG, J. S.; COLLOPY, F. (1998) Integration of Statistical Methods and Judgment of Time Series Forecasting: Principles for Empirical Research. In: WRIGHT, G.; GOODWIN, P., Forecasting with Judgment. Wiley and Sons.
AUER, P.; BURGSTEINER, H.; MAASS, W. (2008) A learning rule for very simple universal approximators consisting of a single layer of perceptrons. Neural Networks. v.21, p. 786-795.
BALLOU, A. R. H. (2004) Business logistics supply chain management: planning, organizing and controlling the supply chain. 5 ed. Upper Saddle River: Pearson Prentice Hall, 789 p.
BATES, J. M.; GRANGER, C. W. J..(1969) “The combination of forecasts”. Operational Research Quarterly. v. 20, n. 4. p. 451-468
BOX, G. E. P.; JENKINS, G. M. (1976) Time series analysis. San Francisco: Holden-Day.
BOX, G. E. P.; JENKINS, G. M.; REINSEL, G. C. (1994) Time Series Analysis, Forecasting and Control, 3rd ed., Prentice Hall, Englewood Clifs, 598 p.
BRASIL. Anuário Estatístico da EMBRATUR, Ministério do Turismo. Brasília. v. 33, 2006. 268p. – available in: http://www.dadosefatos.turismo.gov.br/ dadosefatos/home.html. Access in 18/02/2011
BRASIL. Anuário Estatístico da EMBRATUR, Ministério do Turismo. Brasília. v. 34, 2007. 126p. – available in: http://www.dadosefatos.turismo.gov.br/ dadosefatos/home.html. Access in 18/02/2011
BRASIL. Anuário Estatístico da EMBRATUR. Ministério do Turismo. Brasília. v. 32, 2005. 236p. – available in: http://www.dadosefatos.turismo.gov.br/ dadosefatos/home.html. Access in 18/02/2011
BRASIL. Anuário Estatístico de Turismo, Ministério do Turismo. Brasília. v.36, 2009. 136p. – available in: http://www.dadosefatos.turismo.gov.br/dadosefatos/home.html. Access in 18/02/2011
BRASIL. Anuário Estatístico de Turismo, Ministério do Turismo. Brasília. v.37, 2010. 225p. – available in: http://www.dadosefatos.turismo.gov.br/dadosefatos/home.html. Access in 18/02/2011
BUNN, D. W.; SALO, A. A. (1996) “Adjustment of Forecast with Model Consistent Expectations”. International journal of Forecasting. v.12, p. 163-170.
BUNN, D. W.; WRIGHT, G. (1991) “Interaction of Judgemental and Statistical Forecasting Methods: Issues and Analysis”. Management Science. v.37, n.5. p.501-518.
CHEN, K.Y.; WANG, C. H. (2007) “A hybrid SARIMA and support vector machines in forecasting the production values of the machinery industry in Taiwan”. Expert Systems with Applications. v.32, ed. 1, p. 254-264.
CLEMEN, R. T.; (1989) “Combining forecasts: A review and annotated bibliography”. International journal of forecasting. v. 5, p. 559-583.
COREIA. Korea Tourism Organization – available in: http://kto.visitkorea.or.kr/inout.kto?func_name=search – Access in 15/02/2011
COSHALL, J. T.; CHARLESWORTH, R. (2011) “A management orientated approach to combination forecasting of tourism demand”. Tourism Management. v. 32. p. 759-769.
CostantinI, C.; Pappalardo, C.(2010) “A hierarchical procedure for combination of forecasts”. International journal of forecasting. v. 26, p. 725-743.
DE WILDE, P. (1997) Neural networks models: theory and projects. 2. ed. New York: Springer-Verlag. 174 p.
FLORES, J. H. F. (2009) Comparação de modelos MLP/RNA e modelos Box-Jenkins em séries temporais não lineares. Masters dissertation. Universidade Federal do Rio Grande do Sul.
GOODWIN, P. (2000)“Improve the Voluntary Integration of Statistical Forecasts and Judgement.” International Journal of Forecasting. v. 16. p. 85-99.
GOODWIN, P. (2002)“Integration Management Judgement and Statistical Methods to Improve Short-term Forecasts”. Omega. The International Journal of Management Science. v. 30. p. 127-135.
HAIR JR, J. F.; ANDERSON, R. E.;TATHAN, R. L.; BLACK, W. C. (2005) Análise multivariada de dados. 5ed. Porto Alegre: Bookman, 593 p.
HAYKIN, S. (2001) Redes neurais: princípios e prática. 2. ed. Porto Alegre: Bookman, 900 p.
JAPÃO. Japan Tourism Marketing Co. – available in: http://www.tourism.jp/english/statistics/inbound.php - Access in 15/02/2011
KHASHEI, M.; BIJARI, M. (2010) “An artificial neural network (p, d, q) model for timeseries forecasting”. Expert Systems with Applications. v. 37, p. 479-489.
MORETTIN, P. A.; TOLOI, C. M. C. (2006) Análise de séries temporais. 2 ed. rev. ampl.. São Paulo: Edgard Blücher, 538 p.
PATTON, A. J.; SHEPPARD, K. (2009) “Optimal combinations of realised volatility estimators”. International Journal of Forecasting. v. 25, p. 218-238.
QI, M.; ZHANG, G. P. (2001) “An investigation of model section criteria for neural network time series forecasting”. European Journal of Operational Research. v. 132, p. 666-680.
RIPLEY, B. D. (1996) Pattern recognition and neural networks. Cambridge: Cambridge University Press, 415 p.
SANDERS, N. R.; RITZMAN, L. P. (2001) Judgmental Adjustment of Statistical Forecasts. In: ARMSTRONG, J. S. Principles of Forecasting: A Handbook for Researchers and Practitioners. Kluwer Academic Publishers.
SONG, H.; LI, G. (2008) “Tourism demand modelling and forecasting - A review of recent research”. Tourism Management. v. 29. p. 203–220.
STOCK, J. H.; WATSON, M. W. (2004) “Combination forecasts of output growth in a seven-country data set”. Journal of Forecasting, v.23. p. 405-430.
Werner, L. (2005) Um Modelo Composto para Realizar Previsão de Demanda Através da Integração da Combinação e de Previsões e Ajuste Baseado na Opinião. PhD Thesis. Universidade Federal do Rio Grande do Sul.
WONG, K. K. F.; SONG, H.; WITT S. F.; WU, D. C.(2007) “Tourism forecasting: To combine or not to combine?”. Tourism management. v. 28. p. 1068-1078.
ZHANG, G. P.; BERARDI, V. L. (2001) “Time series forecasting with neural network ensembles: an application for exchange rate prediction”. Journal of Operational Research Society. v. 52, p. 652-664.